溃坝后关联区域损失模型研究
2012-07-19杜丙涛袁永博
杜丙涛,袁永博
(1.中国人民解放军63880部队,河南 洛阳 471003;2.大连理工大学 建设工程学部,辽宁 大连 116024)
溃坝后关联区域损失模型研究
杜丙涛1,2,袁永博2
(1.中国人民解放军63880部队,河南 洛阳 471003;2.大连理工大学 建设工程学部,辽宁 大连 116024)
通过对溃坝后关联区域中区域与区域之间的拓扑关系的研究,从区域之间的关系入手,提出了区域与区域之间的拓扑关系网络。然后,通过其中一个区域发生经济损失对其它区域经济损失的影响,获得其经济损失传播的模型,溃坝后地区的损失范围,损失大小,损失的持续时间的相关关系,并且得到了溃坝后地区的损失收敛的充要条件。最后,对相关的参数进行讨论,提出减少区域经济损失以及传播的相关措施。
溃坝;关联区域;经济损失;传播模型
0 前 言
截至2006年的统计资料,我国己经发生3 498起的溃坝事件。其中,河北“63.8”和河南“75.8”历史大溃坝,前者导致319座坝溃决,冲毁村庄106个,摧毁房屋10×104间,死亡1 467人;后者导致62座坝溃决,其中大型2座,造成113×104hm2耕地和1 100×104人受灾,2.6×104人死亡。溃坝会导致下游居民伤亡、财产损失,还会破坏文化与历史名胜和自然生态环境,给居民带来无法消除的精神痛苦和不良社会影响。堤坝溃决的后果,将会造成很大的损失,在现今经济急速发展的21世纪,社会将越来越关注溃坝的后果。随着我国社会经济的快速发展,堤坝的安全与公共安全息息相关,公众也越来越关注堤坝安全和溃坝后果。因此,对溃坝后造成的损失的研究成为社会所关注的重要课题。
国外发达国家对溃坝后造成的损失的研究自20世纪80年代末就己经开始了。我国在溃坝后造成的损失评价这一方面的研究才刚刚起步。而国内对溃坝后引起的损失评价的研究,主要从一个地区平均的毁坏指标[1-2]或回归分析[3]进行研究的,并没有对区域与区域之间的关联问题进行研究。本文从地区中区域与区域之间的关联关系[4-9]入手,得出了溃坝后地区的损失范围,损失大小,损失的持续时间的相关关系。并且得到了溃坝后地区的损失收敛的充要条件,并对相关的参数进行了讨论,得出一些有意义的结论。
1 模型的建立
溃坝后,会产生很多方面的损失。包括人员伤亡,经济损失,社会损失,环境损失等。由于在本文中,研究的是每种损失发生后在各个关联区域中的影响,而非每种损失本身。而且,研究各种损失在这些关联区域中的影响的方法几乎相同,只是研究每种损失时相关参数不同。所以本文仅以经济损失为例进行论述。
将一个地区分成m×n个区域。一个区域只能受到与它相邻的区域的影响,即这个地区中的任何一个区域只能受到与它邻近上面、下面、左面、右面、斜左上、斜左下、斜右上、斜右下八个方向区域的影响。但是这种经济损失的影响是经济损失大的区域影响经济损失小的区域,经济损失小的区域却不能影响经济损失大的区域。
区域(i,j)受其相邻区域的影响而受到的经济损失为:
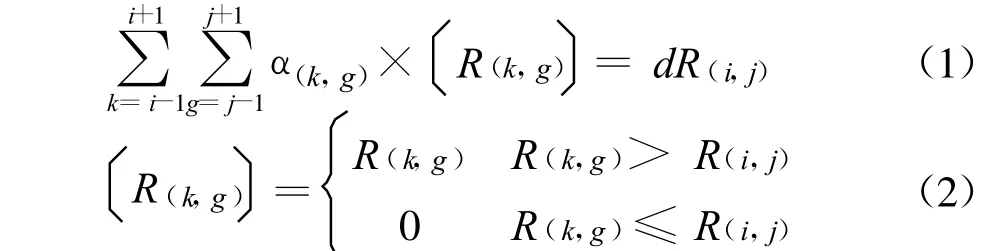
式中:dR(i,j)为区域(i,j)受其相邻区域的影响而受到的经济损失的增加量;R(k,g)为区域(k,g)的经济损失的量;α(k,g)为区域(k,g)对区域(i,j)的经济损失影响系数,一般为大于0且小于1的常数。
当一个区域影响与它相邻的区域时,这个过程不是瞬时完成的,而要经过一定的时间dt,这样将式(1)修正为:
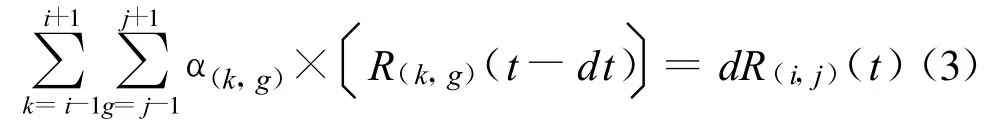
式中:dt为区域(k,g)对区域(i,j)的经济损失影响所经过的时间;t为区域(i,j)所在的时刻;dR(i,j)(t)为时刻t区域(i,j)受其相邻区域的影响经济损失的量;R(k,g)(t)为时刻t区域(k,g)的经济损失的量。
每一个区域都有自身的经济恢复能力,即每一个时刻都可以使经济损失减少一定的量,所以,在时刻t区域(i,j)的实际的经济损失为:

每个区域是在时刻t是按照这样的顺序评价其实际的经济损失的,首先,根据式(2)将周边的8个区域的经济损失的影响进行叠加,得出在时刻t区域(i,j)受其相邻区域的影响经济损失的增加量;然后,将这些影响叠加与前一时刻的损失求和减去自身的经济恢复能力作为这个时间点其最终的经济损失。即:
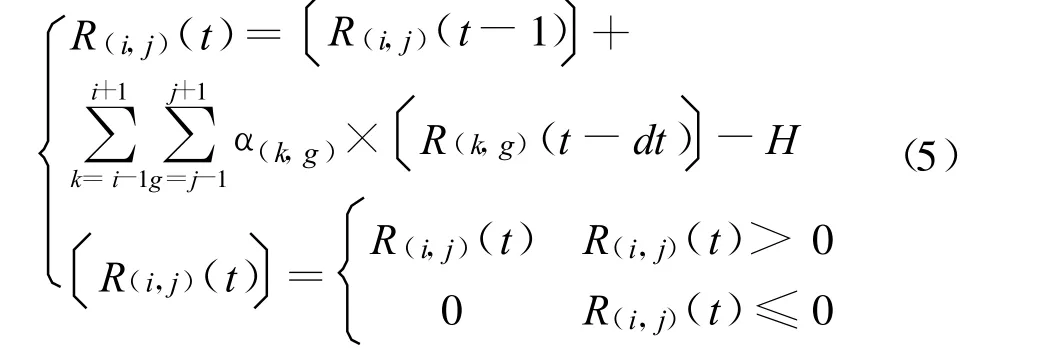
通过对模型的分析,可以知道在这个地区关联区域中,总的经济损失的传播速率就是相邻两个区域的经济损失的传播速率。而在相邻两个区域的经济损失传播的过程中,这个地区中区域的经济损失没有增加,而是以自身的经济恢复能力进行递减。所以,式(5)可以修正为:
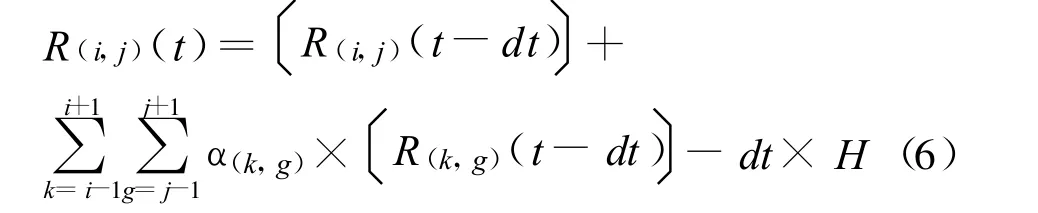
这样,就可以得到一个地区关联区域的经济损失关于空间与时间的关系图。如果设m×n个区域的中心区域为(m0,n0),而溃坝后,直接受到经济损失的只有中心区域(m0,n0)。
设在时刻t,这个地区的区域(it,jt)的经济损失的和最大,区域(it,jt)的集合为P(t)则
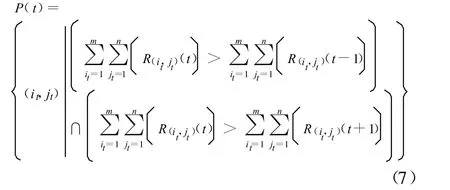
则这个地区的在时刻t时,最大影响范围为

式中:[(imax,jmax),(imin,jmin)]为这个地区的在时刻t时最大影响范围。
则最大影响范围的面积为:
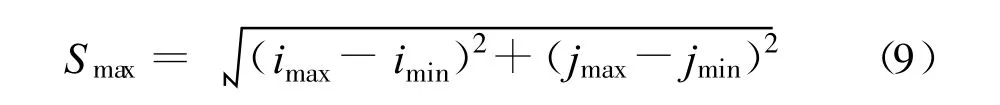
式中:Smax为最大影响范围的面积。
设在时刻T,这个地区所有区域的经济损失都为0。则时刻T的集合为:

定义这个地区的最大影响时间为:

通过最大影响面积Smax和最大影响时间Tmax就可以得出这个地区关联区域总的经济损失。则这个地区关联区域总的经济损失为:

式中:RR为这个地区关联区域总的经济损失。
2 模型的参数分析
如果对于这个地区的所有区域α(k,g)=0,H≠0,由式(5)可知:

式中:R(m0,n0)(0)为溃坝后初始时刻,在中心区域直接受到经济损失。
如果对于这个地区的所有区域α(k,g)≠0,H=0,由式(5)可知:Tmax→∞。
如果对于这个地区的所有区域α(k,g)=0,H=0,由式(5)可知:Tmax→∞。
可见,在α(k,g),H必然存在边界条件使这个地区关联区域总的经济损失收敛。
如果对于离受灾的区域较远的区域来说,其经济损失总是会小于离受灾的区域较近的区域。而且外层受到影响的区域最多为3个区域,如表1所示。

表1 关联区域中受损区域关系表
所以,

如果,经济损失可以由受灾的区域的中心区域向外传播,则必然满足:

如果说这个地区关联区域总的经济损失是有限的,则在受灾的区域的中心区域的经济损失必然是收敛的。
刚开始时中心区域的经济损失总是大于周边的区域的经济损失,由式(2)可知中心区域的经济损失是以H×dt的速率降低,当中心区域的经济损失与周边的区域的经济损失相等时,有:
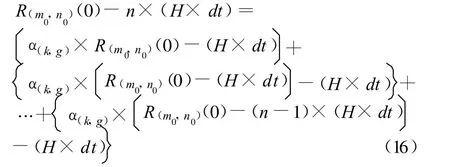
式中:n为当中心区域的经济损失与周边的区域的经济损失相等时,中心区域的经济损失向周边的区域的经济损失影响的传播的次数。
由式(16)可知:
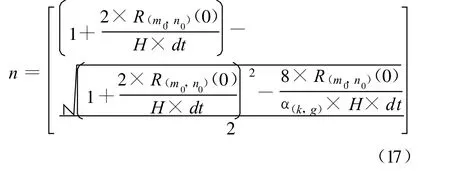
式中:n取整数。
如果从开始到结束,中心区域的经济损失始终大于周边的区域的经济损失,则满足式(18)即可:
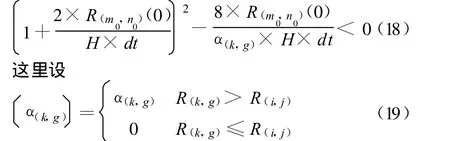
当平衡时,如果使受灾的区域的中心区域的经济损失是收敛的,中心区域的经济损失的增加量必然要小于中心区域的自身的经济恢复能力。由式(16)可知,要满足:
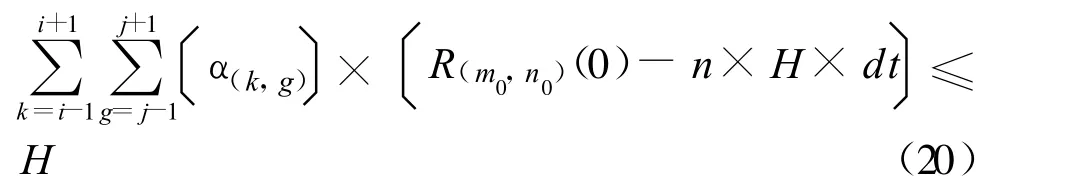
式(14),(15),(18)或(20)为模型的参数的取值范围。
3 模型的求解

-154.56<0
所以,从开始到结束,中心区域的经济损失始终大于周边的区域的经济损失。

表2 参数的选择
则可得到在时刻t,地区的经济损失,如图1。

图1 地区的经济损失图
如果将最大影响时间Tmax内,这个地区关联区域总的经济损失RR与区域(i,j)自身的经济恢复能力H的关系作曲线,可以得到图2。
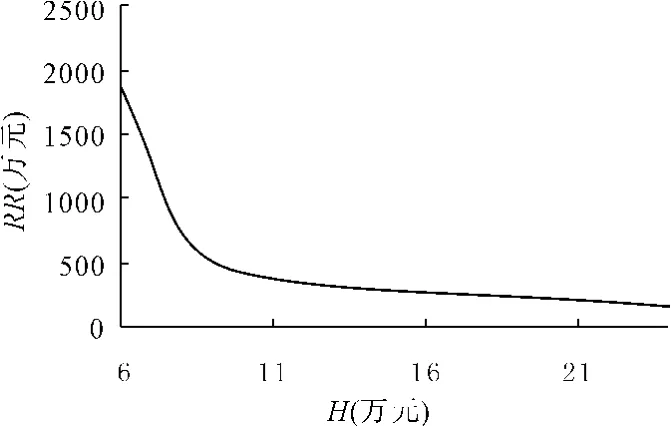
图2 RR与H的关系图
如果将最大影响时间Tmax内,这个地区关联区域总的经济损失RR与区域的经济损失影响系数α的关系作曲线,可以得到图3。
通过对图1,图2,图3的分析,可以知道,这个地区关联区域总的经济损失RR与区域(i,j)自身的经济恢复能力H的关系为指数递减的关系;这个地区关联区域总的经济损失RR与区域的经济损失影响系数α的关系为指数递增的关系。而地区的经济损失是随着时间t呈抛物线型变化。如果取区域(i,j)自身的经济恢复能力H为x轴,区域的经济损失影响系数α为y轴,这个地区关联区域总的经济损失RR为z轴。则可得出三者的三维图,如图4。
同时,可以得出最大影响时间Tmax,最大影响范围的面积Smax与区域(i,j)自身的经济恢复能力H和区域的经济损失影响系数α的关系图,分别如图5,图 6。

图3 RR与α的关系图

图4 RR与H,α的关系图
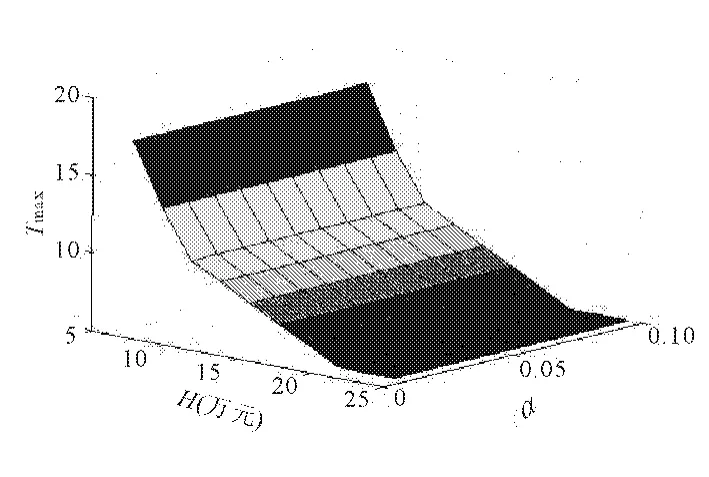
图5 Tmax与 H,α的关系图
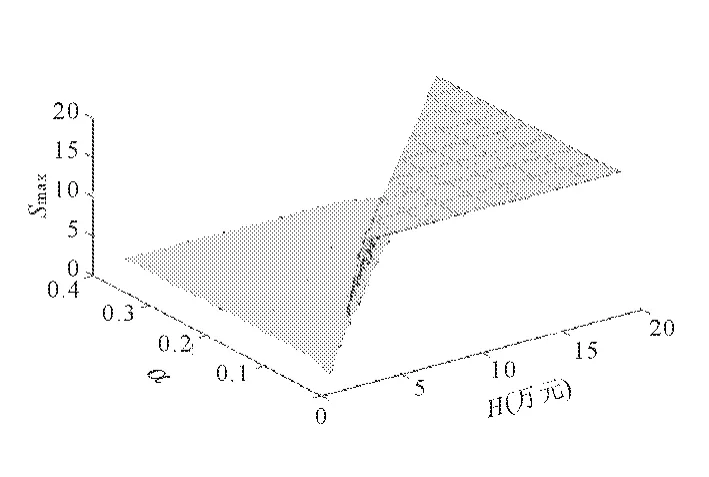
图6 Smax与 H,α的关系图
从图4~图6中可以看出,最大影响时间Tmax和经济损失影响系数α无关,而是随着区域(i,j)自身的经济恢复能力H的增加,而呈指数型减少。同时,可以得出最大影响范围的面积Smax是一个跃阶函数,它随着区域(i,j)自身的经济恢复能力H与经济损失影响系数α呈阶梯型变化。
如果初始时刻,在m×n个区域中,不止中心区域为(m0,n0)产生直接经济损失与它相连的区域也产生了直接经济损失。设R(m0-1,n0)(0)=150,R(m0,n0)(0)=100,R(m0+1,n0)(0)=80。如果取区域(i,j)自身的经济恢复能力H为x轴,区域的经济损失影响系数 α为y轴,这个地区关联区域总的经济损失RR为z轴。则可得出三者的三维图,如图7。可见,与中心区域为一点的变化规律相同。其损失过程中的经济损失的图像如图8。可见,是马鞍型的图形。

图7 RR与H,α的关系图
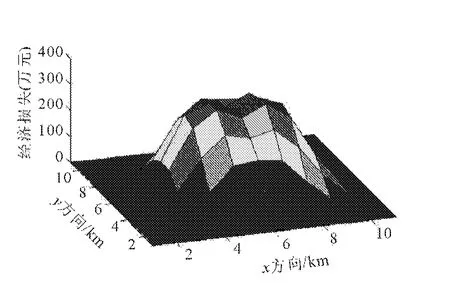
图8 t=10时,地区的经济损失
4 结 论
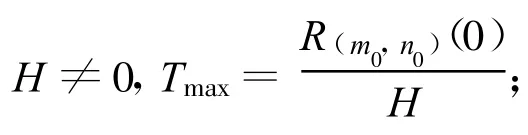
(3)如果这个地区关联区域总的经济损失是有限的,在受灾的区域的中心区域的经济损失是收敛的充要条件为:
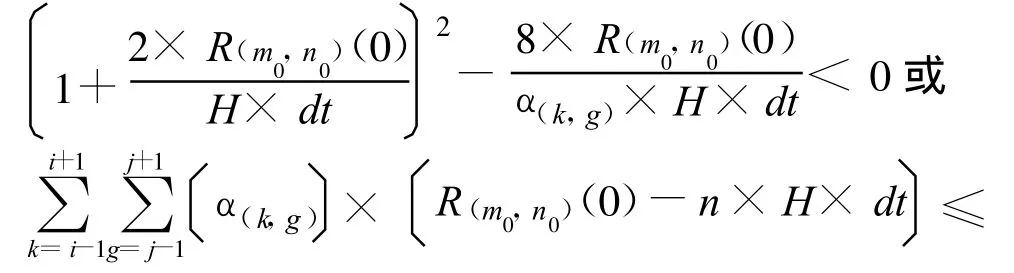
(4)这个地区关联区域总的经济损失RR与区域(i,j)自身的经济恢复能力H的关系为指数递减的关系;这个地区关联区域总的经济损失RR与区域的经济损失影响系数α的关系为指数递增的关系。而地区的经济损失是随着时间t呈抛物线型变化。
(5)最大影响时间Tmax和经济损失影响系数α无关,而是随着区域(i,j)自身的经济恢复能力H的增加,而呈指数型减少。同时,可以得出最大影响范围的面积Smax是一个跃阶函数,它随着区域(i,j)自身的经济恢复能力H与经济损失影响系数α呈阶梯型变化。
(6)如果初始时刻,在m×n个区域中,不止中心区域为(m0,n0)产生直接经济损失与它相连的区域也产生了直接经济损失。这个地区关联区域总的经济损失RR与中心区域为一点的变化规律相同。其损失过程中的经济损失的图像是马鞍型的图形。
[1]李雷,周克发.大坝溃决导致的生命损失估算方法研究现状[J].水利水电科技进展,2006,26(2):76-80.
[2]周一星,陈彦光.城市与城市地理[M].北京:人民教育出版社,2003:84-112.
[3]李雷,王仁忠,盛金宝.溃堤后果严重程度评价模型研究[J].安全与环境学报,2006,6(1):1-4.
[4]Newman M E J,Watts D J.Scaling and percolation in the small-world network model[J].Phys Rev E,1999,60:7332-7342.
[5]E Ahmed,H N Agiza.On modeling epidemics.Including latency,incubation and variable Susceptibility[J].Physica A,1998,253:347-352.
[6]Sirakoulis GCh,Karafyllidis I,ThanailakisA.A cellular automation model for the effects of population movement and vaccination on epidemic propagation[J].Ecological Modeling,2000,133:209-223.
[8]陈森发.复杂系统建模理论与方法[M].南京市:东南大学出版社,2005:153-158.
[9]Taken F.On the numerical determination of the dimension of an attractor,In D.Rand and L S Young,editor,Dynamical Systems and Turbulence[C]//Warwick,1980,Lecture Note in Mathematics,1981,898:361-381.
Study on Loss Model of Relevant Regions after Dam Break
DU Bing-tao1,2,YUAN Yong-bo2
(1.PLA63880Unit,Luoyang,He'nan471003,China;2.Faculty of Construction Engineering,Dalian University of Technology,Dalian,Liaoning116023,China)
Based on the research of the topological relationships among relevant regions,the topological relationship network among relevant regions is put forward,then the spread model for the economic loss after dam break and relevant relationships of the economic loss in dam-break areas are obtained by analyzing the influence of the economic loss in one of the regions upon that in other regions.Furthermore,the parameters of the spread model are discussed,then through this model,the spreading process of the economic loss after dam break is simulated,and the ways for controlling the spreading areas are achieved.At last,some advices are proposed to reduce the loss and control the spreading.
dam-break;relevant regions;economic loss;spread model
F224.0
A
1672—1144(2012)01—0064—05
2011-11-08
2011-12-26
杜丙涛(1979—),男(汉族),河南南阳人,博士研究生,研究方向为工程管理和空间信息技术应用。
