三相异步电动机起动动态过程分析

张立平

(上海海事大学商船学院，上海201306)

1 引言

电动机起动过程的时间不长，但对电机本身和电力系统的影响却很大。特别是船舶电站的容量有限，船上有些辅机拖动系统所采用的电动机的功率接近发电机的单机功率，若直接起动，其起动电流将引起电网电压的很大波动，从而影响其他设备用电设备的正常运行[1]。所以，实际生产过程中对异步电机的起动有一定的要求。为了缩短起动时间，提高生产效率，一般要求异步电机有足够的起动转矩，但起动转矩的加大，必然导致起动电流增大;为了保证电机及生产机械的安全运行和减小对电网的冲击，通常又要求限制起动电流以及起动转矩。电机的起动必须根据拖动系统的具体情况统筹兼顾这两方面的因素，实际应用中，异步电机有着多种起动方法：直接起动、串电阻起动和降压起动[2]。本文建立在异步电动机三相原始动态数学模型上利用MATLAB/SIMULINK来仿真这三种起动方式，观察起动电流、电压、转速、电磁转矩以及机械特性的变化，进一步了解异步电动机的运行特性，比较哪种方式更为理想，更加符合实际情况。

2 异步电动机动态数学模型

异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。在研究异步电动机的多变量非线性数学模型时，为便于分析，常作如下假设：①忽略空间谐波，设三相绕组对称，在空间互差120°电角度，所产生的磁动势沿气隙周围按正弦规律分布。②忽略磁路饱和，各绕组的自感和互感都是恒定的。③忽略铁心损耗。④不考虑频率变化和温度变化对绕组电阻的影响。异步电机的数学模型由下述电压方程、磁链方程、转矩方程和运动方程组成。

三相异步电机的数学模型如下。

以上各式便构成在恒转矩负载下三相异步电机的多变量非线性数学模型[3]。

这是一组变系数非线性微分方程，在用数值法求解时常写成状态方程的标准形式。

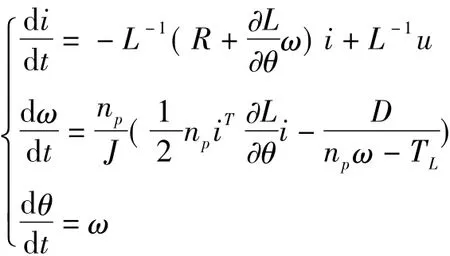
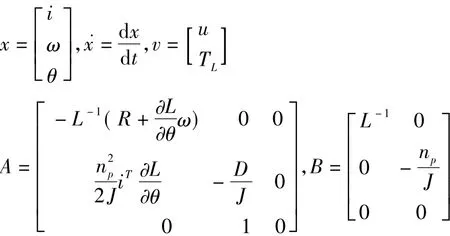
3 Simulink模型实现

实例为一台2.2kW、6极三相异步电动机，电机参数为：定子电阻 Rs=0.435Ω，转子电阻 Rr=0.816Ω，定子、转子相绕组自感 LAA=Laa=0.002H，互感 Lms=0.07H，极对数 np=3，转动惯量 J=0.02kg·m2，旋转阻力系数Romega=0，负载转矩TL=5N·m。电动机在零初始条件下突然接到380V、50Hz的三相对称电源上，由静止开始起动(图1～6)。

图1 三相异步电机直接起动模型

4 机械特性曲线对比

电机拖动原理给出感应电机的机械特性参数表达式[4]：

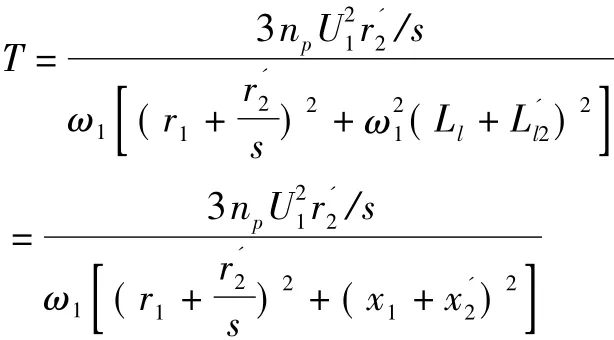
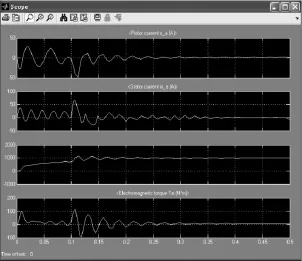
图4 三相异步电机串电阻起动各项运行参数变化

图5 三相异步电机降压起动模型

图6 三相异步电机降压起动各项运行参数变化

式中，T为感应电机的电磁转矩;np电机极对数;U1为电机相电压;r1为定子电阻;为转子电阻折合值;x1为定子漏电抗;为转子漏电抗折合值;ω1为电源角频率;s为异步电机的转差。

根据上式，用MATLAB编辑绘制三相异步电动机定子相电压220V时的机械特性曲线。

分析异步电机机械特性时，用XYGragh画出电机动态转矩－转速仿真曲线，Y轴为电磁转矩，X轴为转速。

图7 三相异步电动机定子相电压220V时的机械特性曲线

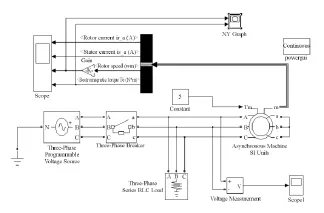
图8 加入XYGragh观察电磁转矩和转速模型

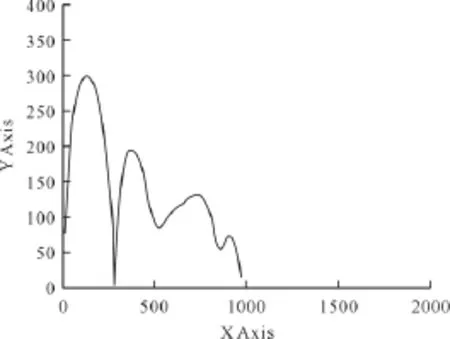
图9 动态转矩－转速曲线

5 结语

由图1～6可知，电机起动瞬时，其起动电流的确很大，是额定电流的5～8倍，总体三种方式对比而言，降压起动的电流波幅相对较小，对电网的冲击影响小。转速、电磁转矩也按实际分析的情况波动上升至稳定。结果可知，直接起动电流波动大，但是稳定时间较短;串电阻起动次之;而降压起动电流冲击小，但是稳定时间较前两者延长。但是，就实际情况而言，0.5s的起动时间对生产影响不大，而起动电流对船舶电网的影响比较大，权衡之下，应采用降压起动。同时，这也符合实际船用电机Y/△降压起动的原因。

由图4～9可知，在电机投入的最初阶段，转矩是振荡的，相应的转速也随着波动，该振荡随时间的推移逐步衰减。因此，起动过程中的动态转矩－转速曲线与稳态的T－s曲线存在明显不同。此外，通过仿真发现，在起动过程中，转子的转速可能会超过同步转速，经过一段时间的衰减振荡，最后达到稳定运行点。仿真结果表明，用Simulink进行三相异步电动机仿真比较方便，且高效直观，得到的结果也是比较接近实际的。

[1]郑华耀.船舶电气设备及系统[M].大连：大连海事大学出版社，2005.

[2]王中鲜.MATLAB建模与仿真应用[M].北京：机械工业出版社，2010.

[3]王秀和.电机学[M].北京：机械工业出版社，2009.

[4]黄忠霖.电工学的 MATLAB实践[M].北京：国防工业出版社，2010.