基于模拟退火粒子群算法的混合动力车参数优化*
2012-07-19邓元望陈可亮鄂加强
邓元望,陈可亮,鄂加强
(湖南大学机械与运载工程学院,长沙 410082)
前言
控制策略是混合动力汽车实现低油耗、低排放的关键所在。逻辑门限控制策略、瞬时优化控制策略、全局最优控制策略和基于模糊逻辑等智能算法的控制策略在国内外得到了较深入的研究[1-5]。由于混合动力汽车的运行模式较为复杂,控制策略还不成熟。目前只有基于工程经验进行设计的逻辑门限控制策略在实际商品化的混合动力汽车上被广泛应用。利用智能算法对已有控制策略进行优化,使优化后的车辆表现出更好的经济性和排放性能,是当前研究控制策略的热点之一[3-6]。粒子群算法(PSO)、遗传算法(GA)、进化算法等已被证明适合应用于混合动力控制参数的优化[7-9]。PSO算法与遗传算法相比具有更高的搜索效率,且算法简单、易于实现。但PSO算法后期受随机振荡现象的影响极易陷入局部极小值,导致精度降低[8]。模拟退火粒子群算法(SAPSO)是将模拟退火(SA)机理应用到PSO算法中,使算法呈现跳跃性,既能保证全局搜索的能力,又能提高计算精度[9]。本文中分别利用多层次参数扫瞄算法(MLPS)和SAPSO算法对逻辑门限参数进行优化,将优化后的车辆在Advisor软件上进行仿真实验,分析燃油经济性和排放性能,并对两种优化方法的优化结果进行了对比分析。
1 逻辑门限控制策略
并联式混合动力汽车驱动系统结构见图1。逻辑门限控制策略具有鲁棒性强、操作简单和易于实现的优点。它通过设定逻辑门限参数值限制发动机和电机的工作模式,使发动机和电机尽可能地工作在高效区。Advisor软件自身携带的并联式混合动力逻辑门限控制策略的控制参数见表1[10]。本文中通过对这些参数进行优化以达到提高燃油经济性和降低排放的目的,并观察电池SOC的变化情况。

表1 逻辑门限参数
在逻辑门限控制策略中,发动机是主要供能装置,电机起辅助作用。具体的控制规则如下:
(6)汽车制动时,电池充电。
式中:ωr、Tr分别为需求转速和需求转矩;vc为发动机低速起动临界转速;Te、Tm分别为发动机和电机提供的转矩;Temax为当前转速下发动机的最大转矩。
2 MLPS算法参数优化
MLPS算法是Advisor软件自身携带的优化算法。其特点是采用单、双立体多层次参数扫描和内置的逻辑来确定适当的参数设置,如图2所示。
多层次参数扫描算法的基本原理是沿下降可行方向,通过逐步缩小区间或反复插值逼近的方法接近最优解。下降可行的条件如下:
式中:f(x)为目标函数;gu(x)、hv(x)为约束条件。
3 SAPSO算法参数优化
3.1 SAPSO算法
PSO算法是基于鸟群捕食行为的群体智能算法,搜索效率高。每一次迭代中通过追踪个体极值和种群极值不断改变自己的速度和位置,其速度和位置可表示为[8-9]
式中:ω(t)为惯性权重;c1、c2为学习因子;r1、r2为分布在(0,1)区间的随机数;分别为粒子 i 在 t 、t+1时刻的速度分别为粒子i在t、t+1时刻的位置;分别为 t 时刻个体及种群最优解,i=1,2,…,d。
PSO算法具有算法简单、易于实现和搜索效率高等优点,但也有“早熟”的缺点,容易陷入局部极小值。本文中针对逻辑门限参数优化这个具体问题,在PSO算法粒子的位置和速度更新过程中加入了模拟退火(SA)机制,计算更新前后的粒子适应度的差值,利用Metropolis准则概率接受搜索结果,使PSO算法呈现跳跃性,得到了SAPSO算法。
3.2 目标函数
SAPSO算法优化的目标是进一步降低燃油消耗和污染物的排放,可描述为[11-12]
式中:X为参数向量;FC(X)为100km燃油消耗;CO(X)、HC(X)、NOx(X)分别为 CO、HC、NOx的排放量;vi(X)>0为汽车必须满足的最高车速、加速性能和爬坡能力等约束条件。逻辑门限参数优化属于多目标优化问题,利用加权法将其转变成单目标优化问题[13]。目标函数F(X)可描述为
式中:δ1、δ2、δ3、δ4分别为 FC(t)、CO(t)、HC(t)、NOx(t)的权重因子;FCz、COz、HCz、NOxz为用户自定义的目标值。
3.3 参数优化实现步骤
SAPSO算法是将SA算法的突跳能力加入PSO算法中,从而在实现全局寻优的同时避免陷入局部极小值。SAPSO 算法优化实现步骤如下[8-9,11-12]。
(1)参数初始化:惯性权重ωstart=0.9,ωend=0.4,加速常数c1=c2=2.0,退火起止温度分别为T=10 000℃,T0=0.01℃,退火速度 K=0.9。
(2)随机产生40个粒子的种群S,即S=40。每个粒子的位置矢量为[p1,p2,p3,p4,p5,p6,p7],位置矢量的 7 个参数分别代表 SOCh、SOCl、vh、vl、mo、mf和mc,并定义每个参数的取值范围。位置矢量的维数D=7,种群S=40,因此该种群可用一个S×D的矩阵表示,矩阵中的每个元素代表一个粒子:
(3)适应值计算:由于逻辑门限参数优化属于约束优化问题,因此适应值函数不同于目标值函数。本文中采用罚函数法将约束优化转变成无约束优化问题[14]。适应值函数可表示为
式中:αvi为第vi个约束的惩罚因子;Evi(X)为与第vi个约束相对应的罚函数。
(4)更新个体极值:对每个粒子,将其适应值J(Xi(t))与个体极值pit进行比较,取优更新为个体极值。
(5)更新全局极值:对每个粒子,将其适应值J(Xi(t))与全局极值pgit进行比较,取优更新为全局极值。
(6)更新粒子的速度和位置:粒子的位置和速度按式(4)和式(5)进行更新,其中惯性权重按式(10)进行线性递减。
式中:tmax、t分别为最大迭代次数和当前迭代次数。
(7)计算更新后的适应值。
(8)引入模拟退火机制:按Metropolis准则接受优化解的同时概率接受非优化解,即计算两个位置所引起的适应值的变化量ΔE;若ΔE<0,则接受新位置;若exp(-ΔE/T)>ε,也接受新位置,否则拒绝,ε为[0,1]之间的随机数;若接受新值,降温,否则返回步骤(3)。
4 仿真结果及分析
采用MLPS算法和SAPSO算法优化后的逻辑门限参数见表2。选用Advisor自身携带的一款并联式混合动力汽车(PARALLEL_defaults_in)作为研究对象,该车发动机和电机的转矩通过转矩耦合器进行耦合,变速器后置,主要结构参数见表3。将MLPS算法和SAPSO算法优化后的逻辑门限参数分别替换Advisor软件默认状态下的参数值,并利用Advisor软件在TEST-CITY-HWY测试循环进行仿真。TEST-CITY-HWY测试是由典型循环FTP-75和HWFET组合而成,能有效地检测车辆的燃油经济性、排放性能和SOC的变化情况。仿真结果如表4所示。

表2 逻辑门限参数优化结果
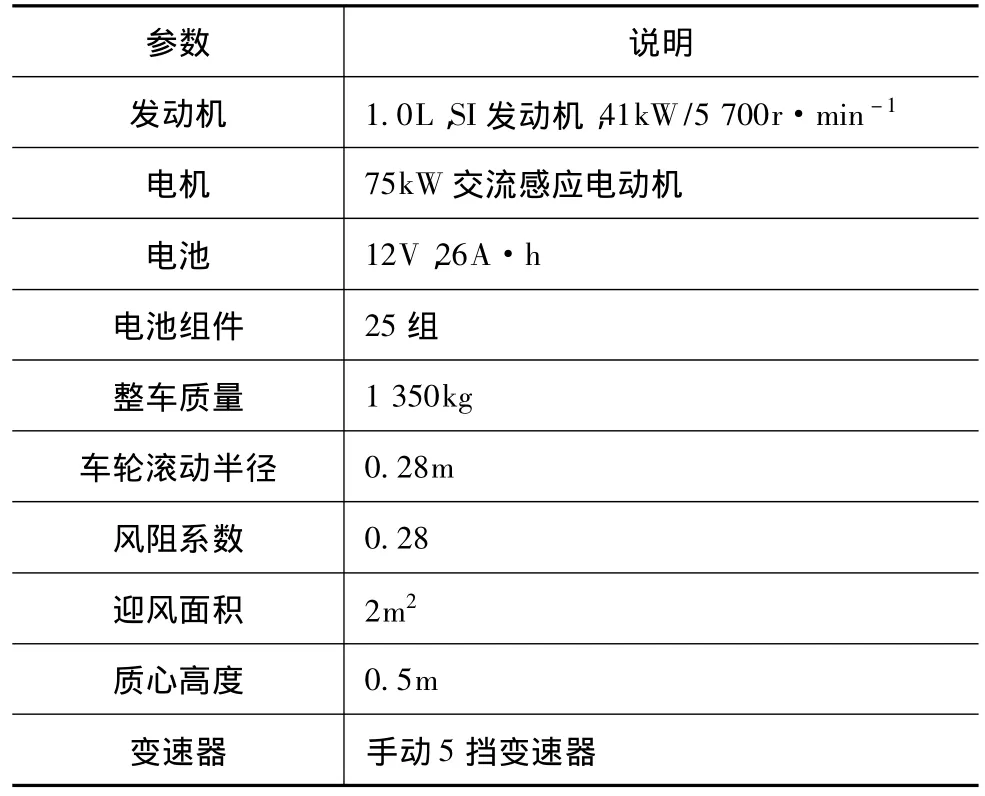
表3 主要结构参数

表4 TEST-CITY-HWY测试结果
由表4可以得出以下结论:采用MLPS算法优化后,燃油消耗和 HC、NOx排放分别下降了11.98%、6.01%、4.03%,但 CO排放增加了25.18%。经SAPSO算法优化后,燃油消耗和HC、CO、NOx排放分别下降了 13.61%、9.57%、27.78%、18.53%。由表4可以看出,经SAPSO算法和MLPS算法优化后车辆性能得到很大改善,且SAPSO算法优化效果更好。
图3~图6为经MLPS算法和SAPSO算法优化后燃油消耗和 HC、CO、NOx在TEST-CITY-HWY测试上的连续变化。图7为SOC在TEST-CITY-HWY测试上的连续变化。由图7可以看出,经SAPSO算法优化后的SOC在测试中要略高些,更有利于提高电池的寿命。图8和图9分别为经MLPS算法和SAPSO算法优化后,车辆在TEST-CITY-HWY测试下运行时发动机的工作情况,由图可以看出,经SAPSO算法优化后,发动机工作点分布明显向高效区移动,有利于降低汽车的燃油消耗和排放。
5 结论
(1)采用MLPS算法对逻辑门限参数进行了优化,由于MLPS算法是Advisor软件自身携带的优化算法,因此操作简单。采用SAPSO算法优化时,首先将多目标问题转化成单目标问题,然后利用罚函数将约束优化转变成无约束优化,最后将SA算法引入PSO算法,实现对逻辑门限参数的优化。
(2)结果表明,经MLPS算法优化后,燃油消耗和HC、NOx排放分别下降了 11.98%、6.01%、4.03%,但CO排放增加了25.18%;经SAPSO算法优化后,燃油消耗和HC、CO、NOx排放分别下降了13.61%、9.57%、27.78%、18.53%,电池的可靠性也明显提高。因此SAPSO算法在混合动力控制参数优化问题上要优于MLPS算法,当对性能要求不高,也可直接采用MLPS算法进行优化。
[1]于秀敏,曹珊,李君,等.混合动力汽车控制策略的研究现状及其发展趋势[J].机械工程学报,2006,42(11):10 -16.
[2]Delprat S,Guerra T M,Rimaux J.Optiaml Control of a Parallel Powertrain:From Global Optimization to Real Time Control Strtegy[C].IEEE 55th Vehicular Technology Conference VTC Spring 2002,4:2082 -2088.
[3]段岩波,张武高,黄震.混合动力汽车模糊逻辑控制策略仿真[J].内燃机工程,2003,24(2):66 -69.
[4]Schouten N J,Salman M A,Kheir N A.Fuzzy Logic Control for Parallel Hybrid Vehicles[J].IEEE Transactions on Control Systems Technology,2002,10(3):460 -468.
[5]Morteza Montazeri-Gh,Amir Poursamad,Babak Ghalichi.Application of Genetic Algorithm for Optimization of Control Strategy in Parallel Hybrid Electric Vehicles[J].Journal of the Franklin Institute,2006,343(4 -5):420 -435.
[6]吴剑.并联式混合动力汽车能量管理策略优化研究[D].济南:山东大学,2008.
[7]吴光强,陈慧勇.基于遗传算法的混合动力汽车参数多目标优化[J].汽车工程,2009,31(1):60 -64.
[8]李丽,牛奔.粒子群优化算法[M].北京:冶金工业出版社,2010.
[9]寇晓丽,刘三阳.基于模拟退火的粒子群算法求解约束优化问题[J].吉林大学学报(工学版),2007,37(1):136 -140.
[10]ADVISOR 2002 Documentation[EB/OL].http://www.avl.com.
[11]Yan Jingyu,Li Chongguo,Qian Huihuan,et al.Multi-objective Parameters Optimization of Electric Assist Control Strategy for Parallel Hybrid Electric Vehicle[C].IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2009:1992 -1997.
[12]Zhang Bingzhan,Chen Zhihang,Mi C,et al.Multi-objective Parameter Optimization of a Series Hybrid Electric Vehicle Using Evolutionary Algorithms[C].The 5th IEEE Vehicle Power and Propulsion Conference,2009:921 -925.
[13]Fang Licun,Qin Shiyin.Concurrent Optimization for Parameters of Powertrain and Control System of Hybrid Electric Vehicle Based on Multi-objective Genetic Algorithms[C].SICE-ICASE International Joint Conference,2006:2424 -2429.
[14]王桂艳.求解非线性约束优化问题的精确罚函数方法[D].北京:北京交通大学,2009.
