汽车喇叭支架振动疲劳分析
2012-07-19刘文华夏汤忠陆志成王萍萍丁超群
刘文华,夏汤忠 ,陆志成 ,刘 盼 ,王萍萍 ,丁超群
(1.神龙汽车有限公司技术中心,武汉 430056;2.湖北三环汽车电器有限公司,武汉 430056)
汽车上许多结构在使用中会受到各种动态载荷的作用,例如安装在前纵梁上的喇叭及其支架,顶盖天窗受到来自路面的位移或加速度激励产生振动,因此在设计时就要考虑到动强度校核,进行相应的振动疲劳耐久性能验证。
振动疲劳是结构所受动态交变载荷 (如振动、冲击、噪声载荷等)的频率分布与结构固有频率分布具有交集或相接近,从而使结构产生共振所导致的疲劳破坏现象,也可以说是结构受到重复载荷作用激起结构共振所导致的疲劳破坏。这时一定的激励将会产生更大的响应,以致更加易于产生破坏,问题涉及到结构共振响应,需要利用结构动力学技术加以研究。
由于结构共振是在动态外载作用下,外力与结构惯性力、弹性力及阻尼力的综合平衡现象,其特点是结构中发生了模态惯性力和阻尼力,其中阻尼力分布是决定结构共振响应大小的重要因素。
本文以某车型喇叭支架的振动试验的破坏状态为例,讨论了喇叭支架系统有限元建模的边界条件和共振阻尼参数的确定和设置,并与试验结果做了对比。
1 喇叭支架振动试验分析
某车型喇叭支架经过一系列振动耐久试验之后发生断裂失效,如图1所示。试验要求如表1所示,正弦扫频范围是5~200 Hz,不同频段内激励的方式和大小不同,分别对XYZ三个方向进行振动试验,每个方向有18个循环的试验。试验从Z向开始,到第14个循环时支架发生断裂,说明原设计方案的喇叭支架疲劳破坏属于低周疲劳问题。试验中测得喇叭支架系统的共振点在22.6 Hz。
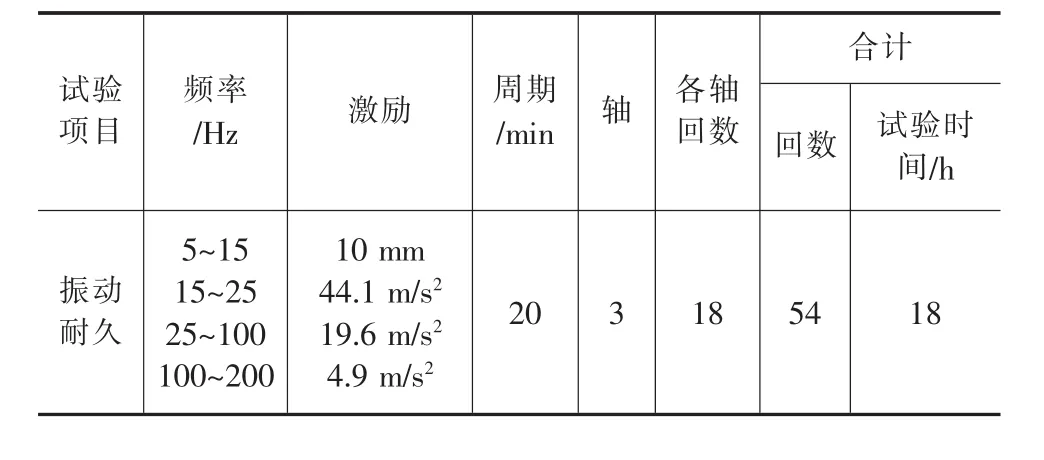
表1 振动试验要求
2 振动疲劳寿命分析
在进行结构振动疲劳寿命分析时,必须了解结构本身的动应力状况,适用的振动疲劳S-N曲线,相应的累积损伤关系式和一定疲劳破坏准则。
2.1 累积损伤关系
对于振动疲劳,大多采用Miner线性累积损伤和式来计算累积损伤量。根据材料的S-N曲线可以计算每个循环所引起的损伤:若加载时间t内由σ1,σ2, …σl这样的 l个不同应力水平构成,Ni为材料S-N曲线上查得的在σi应力水平下的疲劳寿命,ni为σi应力水平下的循环次数,则σi应力水平下的损伤值及总损伤值分别为:
Miner假定D=1时试件将发生疲劳破坏。经验说明这一准则过于保守,特别是对随机振动情况。故有的文献建议D值可以取得稍大一些,例如,对正弦振动D值可取1~1.5,当然D值的实际取法最好由工程使用经验统计和试验研究给出。
2.2 支架疲劳应力标准的确定
根据试验要求可以计算出该试验的整个时间内,每个频段内频率的循环次数 ,如表2所示。通过计算得出5~200 Hz内所有频率的循环次数总和大于106次,共振频率的循环次数小于105。可以判定喇叭支架的振动疲劳试验属于高周疲劳要求。
为了避免喇叭支架低周疲劳破坏,用Neuber理论来确定应力标准。本文中喇叭支架材料的屈服强度200 MPa,其共振频率的应力标准根据Neuber应力计算公式(3)确定为370 MPa。非共振区域的应力标准由准静态应力计算分析获得。
式中:G为剪切模量。
根据公式(4)可以估算材料S-N曲线上对应于表2中各应力标准的疲劳寿命Ni,然后根据公式(1)计算得到每一频段内的疲劳损伤值Di和总损伤值D,如表2中所示,可见该应力标准满足疲劳寿命要求。
式中:S为交变应力值;Se为材料的疲劳极限;b为Basquin斜率。
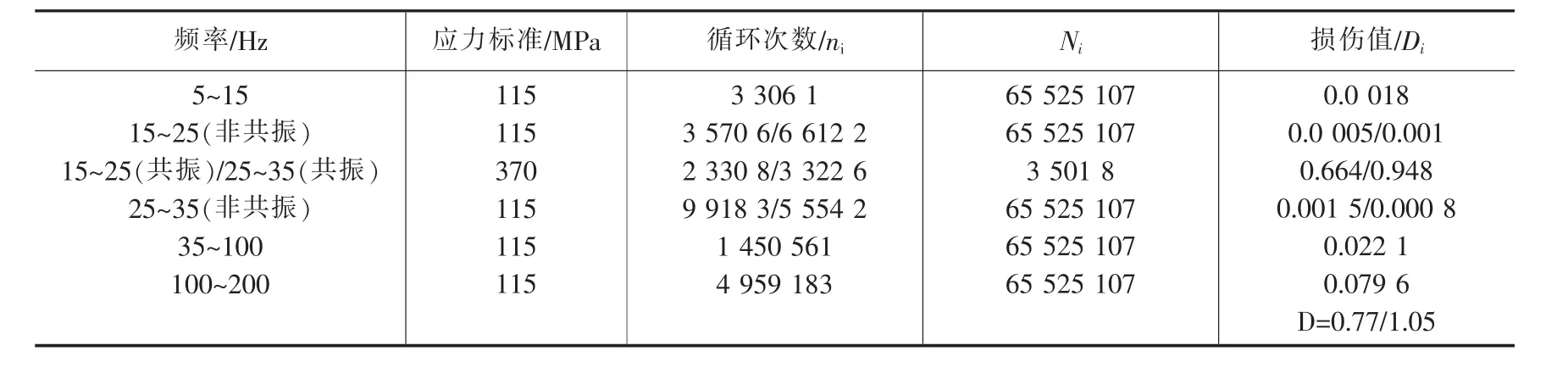
表2 疲劳应力标准与损伤值
从上述疲劳应力标准与损伤值可知,对于共振导致的低周疲劳问题采用Neuber理论进行分析即可,也就是只要共振点的动应力满足一定的要求,其他频率段的应力对振动疲劳的破坏贡献很小。
3 原设计方案的计算分析
3.1 喇叭支架系统的有限元建模
为了寻求解决疲劳断裂的方案,对现有的喇叭及其支架建立有限元模型,模拟喇叭支架的试验边界条件,分别对其模态和响应进行计算分析。
喇叭支架系统主要由支架、减震簧片和喇叭组成。支架与簧片、簧片与喇叭均通过螺钉螺母打紧,支架与簧片采用壳单元划分网格,喇叭、螺钉螺母都用集中质量点简化建模,最终创建的喇叭支架系统的有限元模型如图2所示。
3.2 边界条件的确定及计算分析
试验时,喇叭支架系统通过螺钉固定在刚性试验台架上,如图3所示。为了准确模拟试验的边界条件,尝试了多种约束方式,并且对支架的约束模态做了相应的计算分析,当支架的约束方式如图4所示时,计算所得的支架一阶模态频率与试验结果一致,图5是0~200 Hz模态振型与频率的计算结果,其中第1阶模态频率是22.69 Hz。结合表1中试验条件可以知道,15~25 Hz频段内激励载荷最大,而喇叭支架系统一阶频率刚好在此频段内,且从模态振型上看一阶模态主要是支架和簧片的Z向弯曲振动,可以判断该工况疲劳破坏风险最大。
为了进一步验证上述结论,按照试验条件的激励方式分别对喇叭支架系统做了扫频步长为0.5 Hz的频响分析,结果发现在频率22.5 Hz,加速度激励为Z向44.1 m/s2(4.5 g)时, 动应力最大约为 576 MPa,应力分布如图6所示,应力很大的区域与疲劳断裂区域(图1)相符,进一步验证了有限元模型的建模方法的正确性。
4 改进方案的计算分析
从试验要求来看,最大振动激励载荷在15~25 Hz之间,因此可以通过提高支架悬臂根部刚度来提高一阶模态频率,从而减小共振时动应力水平。经过多次循环迭代,得到了如图7所示的改进方案。
一阶模态频率由原来的22.69 Hz提高到27.44 Hz,模态振型仍为系统的Z向弯曲振动,如图8所示。喇叭支架结构改进后,根据试验要求,一阶频率落在25~100 Hz的频段内,此时加速度激励由4.5 g减小到2 g,再次对喇叭支架系统做扫频步长为0.5 Hz的频响分析,结果发现在频率27.5 Hz时,动应力最大约为149 MPa,远小于370 MPa,因此喇叭支架改进后不存在低周疲劳问题。同时,计算获得改进后疲劳总损伤值D=0.13,说明喇叭支架也不存在高周疲劳问题。
5 计算模型的试验验证
针对提出的改进方案,进行了第二次振动疲劳试验。喇叭支架系统没有发生疲劳断裂,也无任何裂纹产生,此次试验中测得喇叭支架系统响应共振频率为 27.8 Hz。
阻尼大小的选取对响应有很大的影响,在仿真分析中通过大量的计算与试验对比来选取合适的阻尼,最终选取结构阻尼G=0.1。表3是Z向2 g加速度激励下,选取不同阻尼值时共振频率的动应力对比。

表3 不同阻尼的动应力对比
为了验证仿真分析中接触边界、阻尼值的定义是否合适,进行了加速度响应试验测试。试验中,给台架Z向3 g的加速度激励,传感器布置在簧片与喇叭连接螺母上,测得27 Hz时的加速度约为10 g。图9是仿真分析中不同阻尼对应的螺栓连接中心点的加速度曲线,当结构阻尼为0.1时,27 Hz的加速度值为98 328 mm/s2,与试验吻合较好。
6 结论
本文中某车型喇叭支架系统的断裂主要由结构振动疲劳所致,此外表面加工质量问题也是影响断裂的重要因素。从喇叭支架系统振动工况的整个使用周期来看,该支架系统的破坏属于高周疲劳,可以用疲劳累积损伤公式进行损伤计算,但是由于喇叭支架的振动疲劳主要是由共振引起的,因此在做疲劳分析时可以主要关注共振带内的动应力值。
计算分析中还发现,在不同的试验载荷状态下,产生了试验固定边界接触刚度的非线性。因此不同载荷边界条件下,其共振频率也有所不同。同时,在做动力响应分析时要注意选取合适的系统结构阻尼,该阻尼在很大程度上影响着共振点的响应,进而影响到疲劳分析结果的可靠性。
振动疲劳法考虑了构件的动态特性,疲劳破坏的部位往往都是局部共振中应力较大的部位,此方法综合考虑结构共振与应力集中的同时作用,这用准静态法是很难解决的。
[1]姚起杭,姚军.工程结构的振动疲劳问题.应用力学学报,2006,23(1):12-15.
[2]姚起杭,姚军.结构振动疲劳问题的特点与分析方法[J].机械科学与技术,2000,19(增刊):56-58.
[3]徐刚,周鋐,陈栋华,魏传峰.轿车后桥疲劳寿命的数字化预测研究[J].汽车技术,2007,4:29-31.
