基于排列组合熵的表面肌电信号特征分析

袁 明，罗志增

(杭州电子科技大学智能控制与机器人研究所，浙江杭州310018)

0 引 言

对人体肢体动作的识别，依赖于对人体表面肌电信号的特征提取，随着研究的深入，人们发现肌电信号具有混沌的特点［1］，单纯的线性变换不足以描述肌电信号的特征，越来越多的非线性算法开始运用于肌电信号。目前肌电信号的非线性算法主要有分形维、Lyapunov指数和Kolmogorov熵。如利用分形维识别了前臂的臂内旋和外旋［2］;利用Renyi熵、小波熵和复杂度成功的运用于对肌肉疲劳程度的评价［3］。这些算法都可以很好的解决肌电信号的特征提取问题，然而这些特征提取方法普遍抗噪能力弱。在特征提取前需要消除噪声。为了消除噪声，需要复杂的数据预处理过程，而这往往忽略了信号的一些细节。排列组合熵(Permutation Entropy，PE)作为一种基于复杂性量度的非线性动力学参数，其特点是计算简单快速，抗噪能力强，只需要较短的序列长度就能估计出较稳定的系统特征值。非常适用于有实时处理要求的场合。目前排列组合熵在脑电信号处理、心电信号处理、语音识别、气候复杂度、图像处理方面都取得了良好的效果。本文引入排列组合熵来研究不同动作模式下的肌电信号，通过对该算法的研究，利用手部腕上翻、腕下翻、展拳和握拳4类动作下的肌电数据，通过计算各类动作模式下的排列组合熵，构成特征向量，取得了良好的区分效果。

1 基本原理

1.1 排列组合熵

排列组合熵是一种类似于Lyapunov指数的参数［4］，其原理基于相邻数据的对比，适用于任意现实的数据，特别适用于非线性的数据，具有很好的鲁棒性。对噪声有很好的抑制作用，而且这种方法计算简单、计算速度快。排列组合熵的基本原理如下:

给出任意的一维时间序列{xi}i=1，…，T，在长度为T的时间序列排列中，每隔一个样点取连续的n的样点组成 n维的矢量 Xi，Xi=［x(i)，x(i+1)，…，x(i+n－1)］，将 Xi进行升序排列［x(i+j1－1)≤x(i+j2－1)≤，…，x(i+jn－1)］，向量 Xi的排列组合方式为(j1，j2，…，jn)，是 n!种排列组合方式中的一种方式。对整个时间序列中，各个排列组合的排列顺序进行概率统计:

#表示个数，表示任意一种的排列组合方式。

对n≥2，由熵的定义计算出排列组合熵:

排列组合熵描绘了时间序列的n个连续值比对的信息。显然0≤H(n)≤log2n!，如果时间序列中值出现一种可能，那么H(n)=0，如果所有时间序列都不相同，那么H(n)=log2n!，从式2可以看出，时间序列排列越随机，排列组合熵的值越大，时间序列排列越规则，排列组合熵的值越小。排列组合熵反映并放大了时间序列{xi}的变化。

1.2 肌电信号特征比较

为了验证排列组合熵在表面肌电信号中的适用性，本文将小波包熵作为肌电信号的特征与排列组合熵进行比较。小波包熵描述信号的幅值，信号幅值大，该信号能量占总能量之比大，则反映出的小波包熵值大，反之则小波包熵值小;而排列组合熵值是衡量复杂度的一个参数，序列越规则，则排列组合熵值越小，反之序列越随机，则排列组合熵值越大。

本处取1个健康男性手部上翻时尺侧腕伸肌的表面肌电信号(频率f=2.5kHz)，对采集的信号加窗N，求出小波包熵、排列组合熵，然后窗口每移动一个数据点就求出该窗的上述特征值，进行比较，此处取N=100。排列组合熵的维数n=4，小波包熵的小波函数取db4小波，分解层数取m=3。结果如图1所示。

图1 肌电信号的几种特征比较

从图1可以看出，小波包熵和排列组合熵都可以反映肌电信号的特征。肌肉从舒张到收缩，排列组合熵从大到小，说明肌电信号动作时比无动作有规律，而且从图1上可以看出在信号起始和结束无动作阶段，小波包熵幅度变化大，排列组合熵比较平稳，说明排列组合熵具有很好的抗干扰能力。经过多次测试，排列组合熵所用时间仅是小波包熵的1/10。

所以，排列组合熵算法简单，抗干扰能力强，在肌电信号中运用排列组合熵比较合适。

2 实验过程与分析

2.1 信息预处理

本次实验采用美国Noraxon公司的肌电信号采集仪、装有Noraxon肌电处理软件的计算机。实验前，将一次性使用肌电电极放于健康男性受试者的前臂尺侧腕伸肌和尺侧腕屈肌处，用于采集表面肌电信号。采集的SEMG分为4类，分别对应4种手前臂动作:腕上翻，腕下翻，展拳和握拳。每类动作信号40组。

2.2 排列组合熵和小波包熵分布

共采集4类动作信号，160组数据。经过实验测试，8种信号动作持续大约1s，记录2 500个点。本试验取排列组合熵维数n=4。小波包熵的小波函数取db4小波，分解层数取m=4。

任取4类动作信号各10组，每组动作信号包括了屈肌和伸肌两个肌电信号，分别用式2计算各自排列组合熵，以屈肌排列组合熵为横坐标，伸肌排列组合熵为纵坐标，生成坐标系上的一点，同理用小波包熵公式计算各自的小波包熵生成坐标系上的一点，结果如图2所示。并计算各自的均值和标准差系数，结果如表1所示。

图2 排列组合熵和小波包熵分布

图2中，排列组合熵和小波包熵具有相似的分布，不同动作在平面上有着相对独立的聚类区域，类区分性较好;但表1中，相对于小波包熵，排列组合熵聚合度更大，类区分性更好，所以更容易得到理想的分类结果。最后运用K－均值算法获得识别结果［5］。

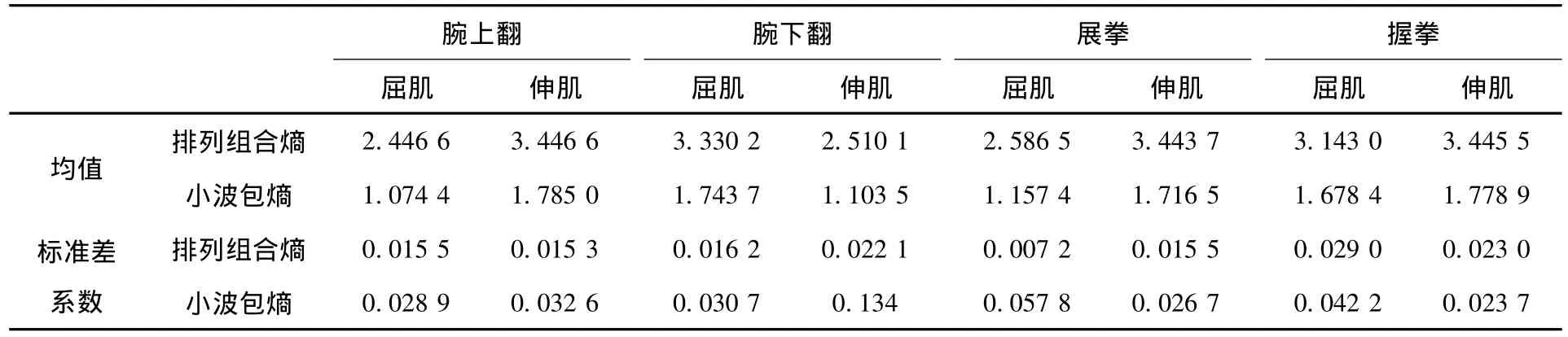
表1 4种动作肌电信号的排列组合熵与小波包熵统计特性

3 结束语

本文运用排列组合熵对腕上翻、腕下翻、展拳和握拳4类前臂动作过程中的2路表面肌电信号分析。研究表明，排列组合熵可以从较短的时间序列中揭示出不同动作肌电信号的复杂性，很好的反映了肌电信号的细微变化情况，计算简单，抗干扰能力强，特别适合于有实时处理要求的场合，是一种较适用于肌电信号特征提取方法。

［1］ 刘加海，王丽，王健.基于相空间、熵和复杂度变化的表面肌电信号分析［J］.浙江大学学报(理学版)，2006，33(2):182－186.

［2］ Hu Xiao，Wang Zhizhong，Ren Xiaomei.Classification of forearm action surface EMG signals based on fractal dimension［J］.Journal of Southeast University，2005，21(3):324 －329.

［3］ 肖毅，陈善广.基于熵理论和复杂度的肌电信号分析［J］.科技导报，2009，27(21):77－81.

［4］ Bandt C，Pompe B.Pemutation Entropya Natural Complexity Measure for Time Series［J］.Phys Rev Lett，2002，88(17):1 595－1 602.

［5］ 杨淑莹.模式识别与智能计算［M］.北京:电子工业出版社，2008:253－254.