基于进化神经网络的电力变压器故障诊断

杜丽艳，魏国华

（秦皇岛电力公司，河北 秦皇岛 066004）

0 引 言

作为现代电力系统中的一个重要组成部分，变压器承担着电力传输和分配的任务。电力变压器的早期故障诊断是防止变压器电气绝缘恶化而产生严重系统停运的一项重要措施。因此，变压器必须严格进行定期检查，以发现早期故障，并防止它们进一步恶化。

变压器油中溶解气体分析（Dissolved Gas Analysis，DGA）技术［1－4］一直被认为是诊断电力变压器早期故障的有效手段。然而，这种方法本身存在一定程度的不完善，甚至对于同一组DGA数据，采用不同的方法，有时会得到不同的诊断结果［5］。另外，变压器结构的复杂性以及故障原因、故障现象和故障机理的多样性，也使得其绝缘故障诊断存在许多困难。

文献［5－8］提出了专家系统法。专家系统是总结各方面专家经验和实践经验，形成规则，利用规则的匹配关系，诊断故障原因和部位。这方面的应用，有很多成功的先例，但是ES有两大局限性：（1）知识获取的“瓶颈”问题；（2）诊断推理不确定性问题。

由于优越的学习和泛化能力，以及在实际应用中的内置容错性，人工神经网络（ANNs）［6－8］已被提出来解决变压器故障诊断问题。ANNs可以通过新增样本训练获取新经验。此外，ANNs通过BP算法进行训练，具有良好的诊断能力。然而，ANNs至今留下了一些尚未解决的问题，如局部训练收敛慢，需要人工确定网络结构和参数等问题。

因为典型的搜索空间往往具有局部最小，基于遗传梯度的BP算法可能停滞在这些潜在的局部最优解中，削弱了ANNs的性能。本文所提的进化算法具有全局搜索能力，可以同时确定神经网络的最佳连接权重和偏置，也避免了基于遗传算法的局限性。因此，ENNs可以准确地捕捉多种溶解气体和故障类型之间的复杂关系，以改善现有的人工神经网络方法的不足。

1 神经网络

图1给出了文献所提的电力变压器故障诊断的神经网络，同层节点之间没有连接，前一层与后一层之间相互充分连接。对于输入信号，先前向传播到隐节点，经激活函数作用后，再把隐节点信息传播到输出节点，最后由输出节点给出结果。对于激活函数要求是可微、非减的，通常采用Sigmoid函数f（u）＝1/（1＋e－u）。网络通过误差反向传播，不断自动学习，修改各节点的连接权和相应节点的阈值。

图1 神经网络

在以下的计算中n、h、k分别表示输入层、隐藏层、输出层的节点，净输入net被定义为输入信号减去偏置的加权总和。隐藏层的节点净输入neth表示如下：

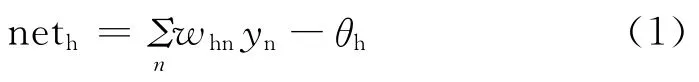
式中，yn为输入层节点n的输出；whn为输入层的节点n到隐藏层节点h的连接权；θh为隐藏层中节点h的偏置。

本文中Sigmoid函数被选作为激活函数。因此，在隐藏层中节点h的输出yh可以描述为：

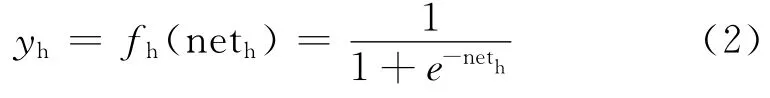
隐藏节点的输出通过另一套连接权传输到输出层的节点。输出层节点k的输出，也可以表示为：

式中，θk为输出层中节点k的偏置。

在神经网络产生预期的结果之前，参数（连接权和偏置）由学习的进程来决定。

广义Delta规则被用来调整节点之间权重的大小，通过最小化以下误差函数E：

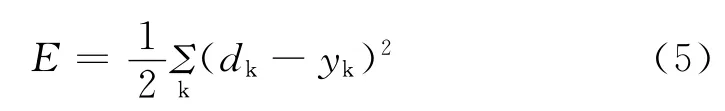
式中，dk为节点k的预期输出结果yk，它是输出层节点k的计算输出结果。

通过遗传梯度算法训练数据，权重wkh不断的更新迭代使E最小化。

式中，i为迭代次数；η为学习效率；α为变量。

类似的，权重whn表示如下：

2 进化算法

如图2为进化神经网络（ENNs）的原理图。本文所提的进化算法流程图如图3所示，用来调整神经网络的参数，即连接权和偏置。

图2 ENNs示意图

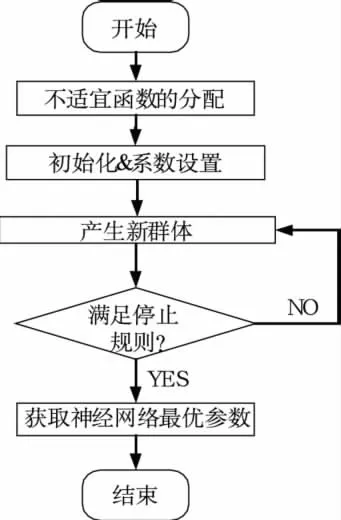
图3 进化算法流程图

2.1 不适应度函数

本文定义了最小平方误差函数Fi，用来表示ENNs与个体Vi之间关系的不适应度值，表示如下：

式中，ykp为第p个样本向量ENNs的第k个计算出处结果；P为样本向量的总数；dkp为相应的第k个输出节点的实际故障指示（“1”表示有故障，“0”表示无故障）。

2.2 初始化

最初的父实验向量Vi，i＝1，2，…，I是通过对Vi中每个元素的设置，从每一个维度的合理范围内随机生成的，表示如下：

式中，U（Admin，Admax为均匀分布的随机变量。

2.3 后代创造

把带有零均值的高斯随机变量与标准差相加，每个父实验向量Vi，i＝1，2，…，I产生一个子向量Vi＋1，也就是：

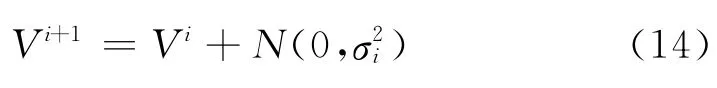
式中，Fi为式（12）中与实验向量Vi相关的不适应度函数；Sf为规模系数；Os为偏差。

2.4 竞争和选择

在进化算法中竞争与生存机制是随机的。父代和其产生的子代与其它随机选择出来的个体竞争从而在它们的不适应度值中获胜。对每个个体来说获胜的标准表示为如下：

式中，Wi为第i个个体的得分；Nc为随机选择的竞争者的数量；Fi为第i个个体的不适应度值；Fk为第k个竞争者的不适应度值。

当所有个体参与竞争以后，父代和其产生的子代根据与Wi的值相对应的辈分顺序进行排列。然后，第一批胜出个体们和他们所对应的不适应度值被选出来作为下一代新的父代。

2.5 停止规则

最为满足最高辈分的停止规则或者式（12）中的最小值标准，进化进程结束，并且具有最低不适应度值的解决方案作为故障诊断的最佳ENNs。否则，重复之前详细介绍的后代创造与选择过程。

3 算例测试

ENNs针对820条实际的气体记录进行测试，测试记录来自某供电公司的172台10 kV变压器。故障类型由该公司的诊断专家确定，依据多种DGA方法，小组讨论和所怀疑变压器的内部检查。表1把总共820个训练样本分成5类变压器故障。设计了两个案例来评估本文所提出的诊断系统的准确性。案例Ⅰ选择了广泛使用的三种气体比率，C2H2/C2H4、CH4/H2和C2H4/C2H6，作为输入变量。案例Ⅱ利用五个气体的浓度，H2、CH4、C2H6、C2H4和 C2H2，作为输入变量对可能出现的故障类型进行分类。

表1 820个实际训练数据组成

IEC/IEEE标准DGA方法，模糊诊断系统（FDS）和基于BP算法训练的多层人工神经网络应用到相同的数值数据库中进行比较。相同数量的输入、隐藏和输出节点分别给予到ENNs和ANNs模型中。神经网络中隐藏节点的数目经反复试验确定，其中最好的被用来诊断。

FDSⅠ和FDSⅡ分别采用了3个和5个输入属性，每个属性包括三个模糊分区（小型、中型、大型）。表2列出了ENNsⅠ和ENNsⅡ的参数设置。ANNⅠ和ANNⅡ的参数分别与ENNsⅠ和ENNsⅡ相同，梯度遗传方法的使用除外。根据所开发的系统对三种类型的性能进行了评估：训练数据的学习能力，测试数据的泛化能力及错误包含数据测试。

表2 ENNs参数集

3.1 学习能力测试

神经网络的构造时间随着1到20隐藏节点的数目比例增加，但是模型的准确性却不能按比例提高。当隐藏节点的数目超过8个（Ⅰ）和12个（Ⅱ）的时候出现饱和节点。因此，这些隐藏的节点分别被选来用作Ⅰ和Ⅱ的诊断。

表3根据820个实际样本数据，比较了ENNs与现有其它方法的学习能力。结果表明所提出的ENNs方法在Ⅰ和Ⅱ中明显地要比其它方法更加准确。由于进化算法的全局搜索能力，ENNs的构造时间要远小于ANNs方法的构造时间。值得注意的是，在Ⅱ中，FDS方法和ANNs方法的额外构造时间会随着输入变量的增加而大大增加，但我们所提出的ENNs增加比较缓慢。

表3 以820条实际气体记录为依据不同方法的性能评估

3.2 泛化能力测试

使用十折叠交叉验证测试对在新案例下ENNs的发展能力进行了评估。数据分为10组，近似给每组相等数量的数据。其中十组中九组的数据作为训练集，剩下的作为测试集用来诊断系统，它需要被训练来评估系统的准确性。十组中的每一组依次交替来作为测试集。

在表4中，十折叠交叉验证显示，本文所提的ENNs方案一和ENNs方案二在两个案例中分别是精度最高的。此外，ENNs具有较高的诊断准确率，案例一中为91.83%，案例二中为95.12%。这个发现证明了ENNs比目前存在的其它方法在学习新事物的泛化能力方面更优越。

表4 十折叠交叉验证下诊断准确率

3.3 错误包含数据测试

DGA的气体数据由于气体产生的位置不同，故障类型多样性，不同环境产生的气体溶解度的变化，油样、气体采集、色谱分析本质上存在的错误等，可能会包含一些错误或者不确定因素。测试数据集是由随机和均匀分布的样本与训练数据相加得到的，用来评估ENNs的容错能力。

对于不同数量的增加错误的测试结果列于表5中。如表中所示，含有错误的数据降低了诊断的准确性，然而，三个诊断方法都具有很好的容错性。此外，ENNs是在所有的情况下诊断准确率最高的。

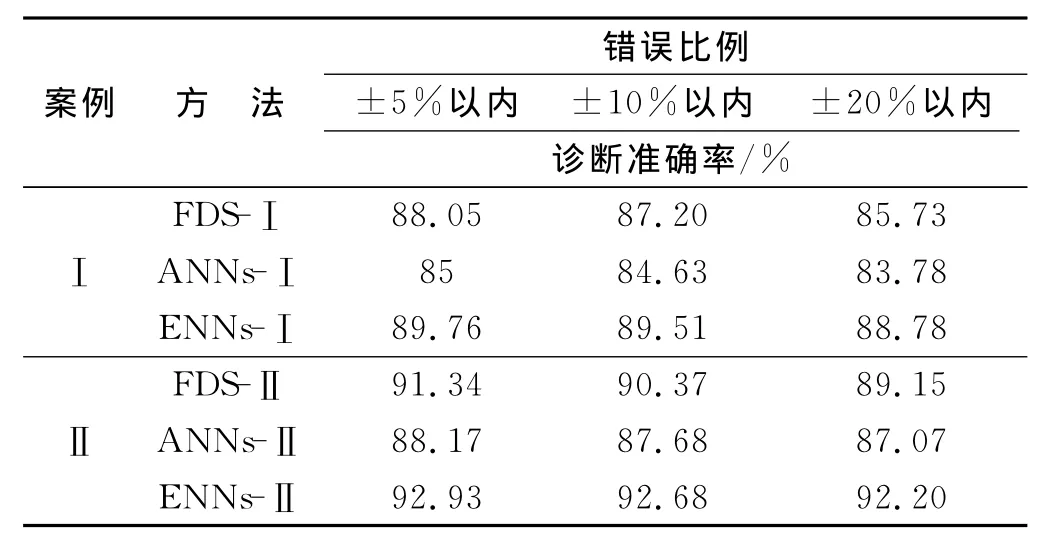
表5 不同比例的增加错误诊断准确率

4 结 论

本文介绍了进化神经网络，增强了电力变压器DGA故障诊断方法。据历史诊断记录，进化算法能自动构造ENNs，并且确定神经网络的最佳连接权重和偏置条件，实现了DGA最准确的诊断模型。因此，ENNs可以准确地捕捉溶解气体含量和相应的故障条件之间的非线性关系。性能评价以某电力公司实际DGA的数据进行测试，并与现有的诊断系统进行比较。测试结果表明，ENNs与传统方法相比提高了诊断准确性和学习速度。

［1］ Chen C S，Hwang J C.Development of simplified loss models for distribution system analysis［J］.IEEE Transactions on Power Delivery，1994，9（3）：1545－1551.

［2］ Pugh P S，Wagner H H.Detection of incipient faults in transformer by gas analysis［J］.IEEE Transactions on Power Delivery，1961，80（3）：189－195.

［3］ Kelly J J.Transformer fault diagnosis by dissolved－gas analysis［J］.IEEE Trans on Ind.Applicat，1980，16（1）：777－782.

［4］ Dornenburg E，Strittmater W.Monitoring oil cooling transformers by gas analysis［J］.Transactions on Brown Boveri Review，1974，61（8）：238－274.

［5］ 王大忠，徐 文，周泽存，等.模糊理论、专家系统及人工神经网络在电力变压器故障诊断中应用——基于油中溶解气体进行分析诊断［J］.中国电机工程学报，1996，16（5）：349－353.

［6］ 王财胜，胡文堂.结合神经网络技术的变压器故障诊断专家系统［J］.中国电力，2001，34（5）：37－40.

［7］ 束洪春，孙向飞，司大军.电力变压器故障诊断专家系统知识库建立和维护的粗糙集方法［J］.中国电机工程学报，2002，22（2）：31－35.

［8］ 徐 文，王大忠，周泽存.基于模糊理论的变压器故障诊断专家系统［J］.电力系统自动化，1995，19（6）：32－37.