超导重力仪观测数据分析①

聂仁奇，章传银，秘金钟

（1.中国测绘科学研究院，北京100830；2.山东科技大学，山东 青岛266510）

0 引 言

地球时变重力场包含地球系统物质分布及其运移的丰富信息，直接反映了地球各圈层最基本的物质及其变化特性，是各种环境变化导致地球动力学特征最基本、最直接和最重要的物理量之一。时变重力场观测信号是深入研究、了解全球和局部动力学特征、固体地球内部的构造和运动特征、各圈层的相互作用和耦合机制的重要信息源［1]。目前超导重力仪具有很高的灵敏度和稳定性、很低的噪音水平和漂移以及很宽的动态频率响应范围，是目前观测精度最高的重力仪。因此，超导重力仪作为研究时变重力场的关键仪器。探测时间序列中隐含的周期信号是超导重力仪观测数据分析的主要目标之一，通过快速傅里叶变换（FFT）和最小二乘谱分析方法分析超导重力数据中隐含信号的检测，两种方法结果进行了分析比较。最终用小波分析的方法进行了检校。

1 超导重力数据

1.1 数据获取

获取的数据是一台GWR台站式超导重力仪的数据，以1min的采样频率进行数据采集，并以1d作为一个记录文件，观测数据为电压（V），这些数据乘以一个系数（不同的测站其系数不同）即可转化为重力值（单位μGal）。这个超导重力仪的系数为－76.504μGal／V.

1.2 重力潮汐改正

受日月引潮位作用影响重力产生周期性的潮汐变化即为重力潮汐。在重力观测中包含了非常显著的重力潮汐变化，其幅度可以超过200，且表现为非常强烈的纬度依赖特征，如果不精确改正，就会严重影响对地球的动力学和环境变化的研究。由重力潮汐预测程序G－wave计算得到重力潮汐理论结果，可以用来剔除超导重力仪原始观测数据中重力潮汐信号的影响。G－wave程序的预测精度（在日月引力作用下）为40μGal.在计算前，应输入测站的经度和纬度，根据理论计算结果，可以从原始数据中剔除重力潮汐的影响［2]。

1.3 数据预处理

由于超导重力仪受到环境的影响（地震，地下水变化）和仪器因素（氦注入、故障、维修、校准、系统升级等），超导重力仪的数据是不连续不稳定的。在原始数据中存在着数据的重叠、断链、尖峰、突跳、漂移及噪声干扰。故在分析前必须删除重叠数据，使数据序列的时间单位呈单调递增。如图1所示，三月份数据中出现了四次比较大的噪音，对结果会产生很大的扭曲，因此，必须将这部分数据删除［3]。

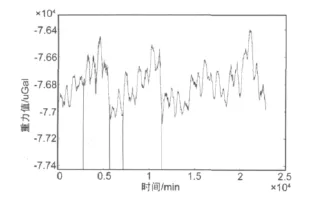
图1 三月份重力数据

2 基本原理与方法

2.1 基于FFT的功率谱分析

FFT是进行超导重力观测数据中隐含信号检测的常用经典方法。FFT算法提供了一种快速频谱分析方法，可直接用来处理离散信号数据。

FFT在处理时间序列数据时要求数据必须等间隔、等权、连续和平稳。但在超导重力数据采集工程中难免出现断链、尖峰、噪音、漂移等特点。造成了数据的不等间隔、不等权、不连续以及不平稳的情况。所以，在用FFT谱分析处理超导重力数据时，必须要对超导重力事先处理的观测数据进行数据预处理。数据预处理的目的在于保证所需信号不受损失，消除干扰因素，从而得到高精度的观测资料。谱分析和时间序列分析都要求原始数据为零均值，没有线性趋势项。为此，需要对时间序列进行线性拟合，即去除时间序列的趋势项。

式中：s为原始时间序列；Sdt为去除趋势项后的时间序列。

利用FFT进行谱分析时要求均匀采样，但在超导重力时间序列中难免出现断链的情况。为了获得均匀采样的时间序列，需要对时间序列进行插值。插值采用拉格朗日插值进行。由此获得了经预处理的时间序列［4]。

对于数据预处理获得的时间序列，达到了等间隔、等权、连续和平稳的要求。用离散傅里叶变换计算功率谱

2.2 最小二乘功率谱分析

用FFT进行频谱分析，研究时间序列中可能存在的周期信号，并比较各种频率波动的振幅或功率，可以确定主要周期。但FFT的不足主要表现在：它要求数据必须等间隔、等权、连续和平稳，对于不满足这些条件的数据处理，FFT采用数据内插（如线性内插）使间断的数据连续，使不等间距数据等间距以及提取趋势项、修正数据漂移等。针对FFT的不足和局限性，Vanicek于1971年提出的最小二乘谱分析（LSSA），将最小二乘逼近原理用于谱分析中，解决了测量数据采集中经常出现的诸如数据序列不等间隔、不等权、不平稳、有断链、尖峰、漂移等需要进行数据预处理的问题。Pagiatakis给出了数据序列不等权情况下的LSSA公式，提出了用数理统计理论检验最小二乘谱的显著性方法［5－6]，并总结出该方法具有如下优越性：①系统误差可以得到严格抑制，而不产生谱峰的漂移；②不等间距的序列不需要预处理；③可以处理具有协方差矩阵的时间序列；④能进行谱峰显著性的统计检验［7]。

在谱分析中，通常将寻找的隐含周期信号表示为一组以正弦和余弦为基函数的线性组合。给定一组观测值向量f＝f（t）＝｛fi｝，i＝1，2，…，n，若设定基函数形式为一组频率ωi（i＝1，2，…，m）的三角函数，则有

其中，Ω 为未知参数向量，设 Ω＝［Ω1i，Ω2i]T，Φ＝［cos（ωit），sin（ωit）]，其中Ω 由公式

其中，Φ为已知基函数向量。

对于不同的频率ωi（i＝1，2，…，m ），可以得到不同的频谱值

这就是最小二乘谱分析的基本思想。显然，f的最小二乘谱是所有频率ωi（i＝1，2，…，m）下的谱值集合，ωi谱值越大，表明f在该频率的功率越大。

具有协方差函数Cf时的最小二乘谱计算公式为

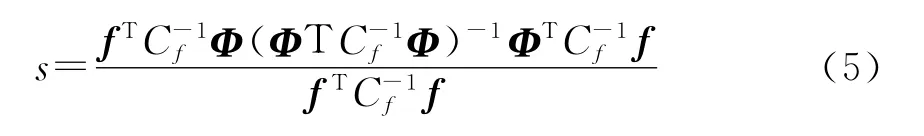
3 实例分析与小波分析校核

3.1 基于FFT的功率谱分析

以2008年1月份的数据为例，进行功率谱的计算。如图2示出的是2008年1月经过去粗差、去趋势项、插值形成的重力值序列。

图2 一月份重力值序列

基于FFT技术，对预处理后的时间序列进行谱分析得到谱值。图3详细示出了2008年1月重力数据功率谱图。

图3 一月份重力数据功率谱

从图3中可以看出四个比较清晰的功率谱峰值，即具有四个很明显的周期项。分别为以67.635h、23.951 5h、11.999 9h为周期和以8.001 2为周期的四个周期项。

3.2 基于最小二乘功率谱分析

最小二乘谱分析可以直接分析不等间隔不等权的数据序列。但对于较大的噪音会对谱分析结果产生扭曲，因此，在数据处理时必须将这部分较大的噪音删除。基于最小二乘谱分析技术，无需内插缺失的数据，无需平滑尖峰和漂移，直接由加权最小二乘谱分析得到谱值。同样也是以2008年1月份的数据为例用最小二乘功率谱分析进行了周期探测。

图4 最小二乘谱分析结果

从图4中可以看出四个比较清晰的功率谱峰值，即具有四个很明显的周期项，这一点和FFT谱分析得到的结果是一致的。从左至右依次为以68.133h、23.991 7h、以12.162 3h为周期和以8.183 1为周期的四个周期项。

3.3 小波多辨分析校核

为了再次说明两种方法的可行性和准确性，利用目前成熟的小波多分辨分析方法对两种计算结果也进行了校核。

图5 小波多分辨分析

图5是超导重力数据时间序列的小波多分辨分析得到的结果。图5中第一行、第二行、第三行、第四行表示的是周期分别为8.030 2h、12.000 0 h、23.936 7h、68h的信号。和由FFT谱分析方法和最小二乘谱分析方法计算得到的结果十分吻合。

分别利用FFT谱分析方法和最小二乘谱方法对2008年1月的超导重力数据进行了分析。主要的周期探测结果如表1所示。

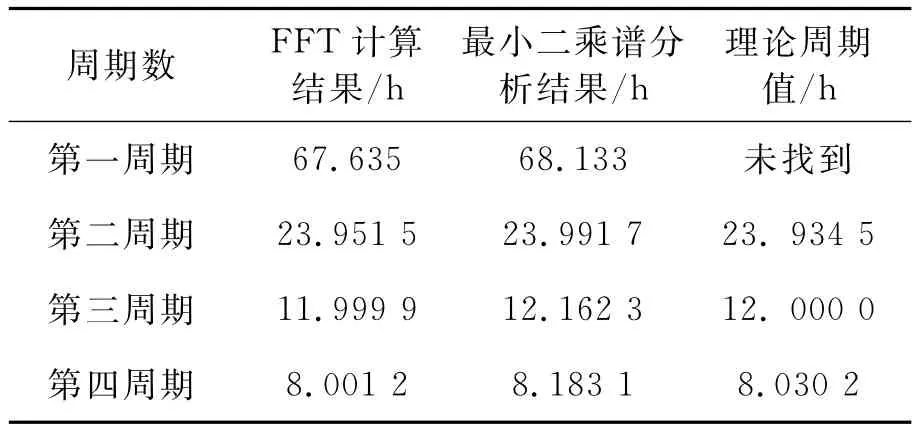
表1 主要周期探测结果

从表1可以看出，利用两种方法计算得到的周期结果与理论结果基本一致，说明了这两种周期探测方法在超导重力数据探测周期中的正确性。

4 结 论

基于超导重力数据研究时变重力场、重力潮汐、自由核章动参数测定、海潮模型有效性检验、大气负荷信号改正、地球自由振荡检测等方面发挥了重要作用。超导重力仪观测序列具有丰富的信息，蕴藏了地球内部变化的所有动态变量的痕迹。分别利用FFT谱分析方法和最小二乘谱分析方法对2008年1月份的数据进行了周期探测。两种方法的计算结果十分吻合，且与理论值也十分接近。总体来看：

1）快速傅里叶变换（FFT）谱分析，计算简单，处理海量数据时有较大优势，可快速探测出观测序列中的隐含周期信号，其计算结果与理论值基本吻合。

2）最小二乘谱分析，对存在断链、不等间隔和不等权数据的频谱分析有较大优势。

［1]尹 晖.SPIROS D P.最小二乘谱及其在超导重力观测数据分析中的应用［J].武汉大学学报·信息科学版，2005，30（7）：613－616.

［2]MERRIAM J B.An ephemeris for gravity tide predic－tions at the Nanogal Level［J].Geophys.J.Int.，1992（108）：415－422.

［3]邢 喆.超导重力仪观测数据的初步分析与信号检测［D].武汉：武汉大学，2004.

［4]陈 晖，周继慧，郭春亮，等.基于VB的FFT算法的设计与实现［J].华东交通大学学报，2003，20（1）：94－96.

［5]PAGIATAKIS S D.Stochastic significance of peaks in the least－squares spectrum［J].Journal of Geodesy，1999（73）：67－78.

［6]CHEN Y Q.Deformation observation data process［M].Beijing：Press of Surveying and Mapping，1988.

［7]WELL D E，VANICEK P，PAGIATAKIS S D.Least squares spectral analysis revisited.Tech.Rep.84，Department of Surveying Engineering［R].University of New Brunswick，Fredericton，1985.