运用迭代FFT算法优化平面稀疏阵列①

张 飞，黄 伟，陈客松

（电子科技大学 电子工程学院，四川 成都610054）

0 引 言

在许多实际工程应用中，只要求天线阵列有窄的扫描波束，而不要求有相应的增益。如高频地面雷达天线、抗环境干扰的卫星接收天线和射电天文中的干涉阵列等。增益与照射口径的面积有关，阵列波束宽度与口径的最大尺寸有关，因此，可以采用稀疏阵列（即从规则的栅格中抽去天线单元或接匹配负载）的方法构造出一个降低增益的高方向性天线阵列，以较少的天线单元数达到扫描波束变窄、空间分辨率提高以及天线单元间互耦减弱等技术指标，从而大大降低生产成本［1]。阵列的周期性变稀会使阵列方向图出现非常高的副瓣，稀疏阵列优化设计的主要目标就是实现旁瓣性能最优化，即尽可能的降低峰值旁瓣电平（PSL）。

近年来，随着计算机技术的飞速发展，高效的阵列优化方法已成为研究热点。用于平面稀疏阵列优化的算法主要有遗传算法、模拟退火算法、粒子群算法以及最近出现的蚁群算法等。这些算法从本质上来说都是基于随机性的自然算法，需要很长的运算时间才能得到优化结果。

介绍了一种基于迭代FFT算法的平面稀疏阵列优化方法。这是一种全新高效的优化方法。在稀疏阵列中，阵列因子与阵元激励之间存在傅里叶变换关系，在旁瓣约束下，对初始阵元激励进行少次迭代，就能使阵列的旁瓣性能得到显著的优化。以阵列大小为10×20的矩形平面稀疏阵列作为优化实例，证实了该方法的高效性和稳健性。

1 矩形平面稀疏阵列模型

一个稀疏率为f、可放置阵元的栅格数（阵列大小）为M×N，栅格间距为dx＝dy＝d的矩形平面稀疏阵列如图1所示。阵元数目为T＝f×M×N.阵列方向图可以表示为

式中：EF（μ，v）为天线单元的方向图函数；又称单元因子；AF（μ，v）为阵列因子；Amn为第（m，n）阵元的激励；k＝2π／λ，λ为波长；μ＝sinθcosφ；v＝sinθsinφ.当阵元均为理想的全向性天线单元，各阵元等幅同相激励，主波束指向阵列法线方向时，EF（μ，v）＝1，平面稀疏阵列的方向图为

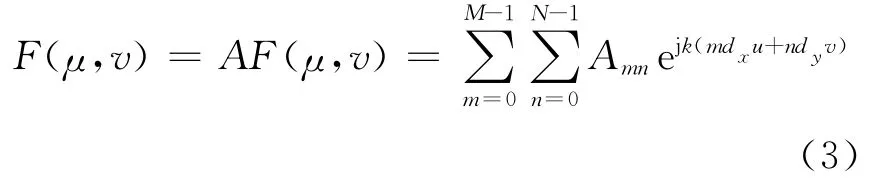
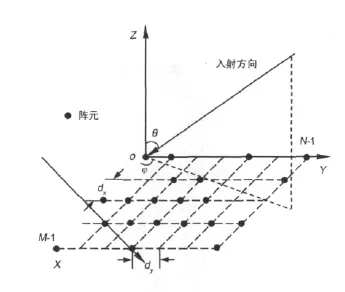
图1 矩形平面稀疏阵列模型

二维离散傅里叶逆变换，可以表示为

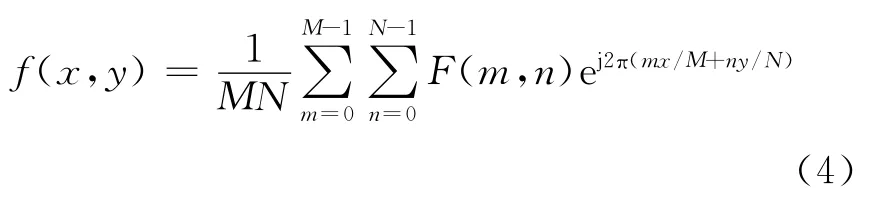
比较式（3）与式（4）可以看出阵元激励Amn与阵列因子AF之间存在傅里叶变换关系。如果优化目标是要获得可视区的峰值旁瓣电平（PSL）最小的矩形平面稀疏阵列，则最优化模型为

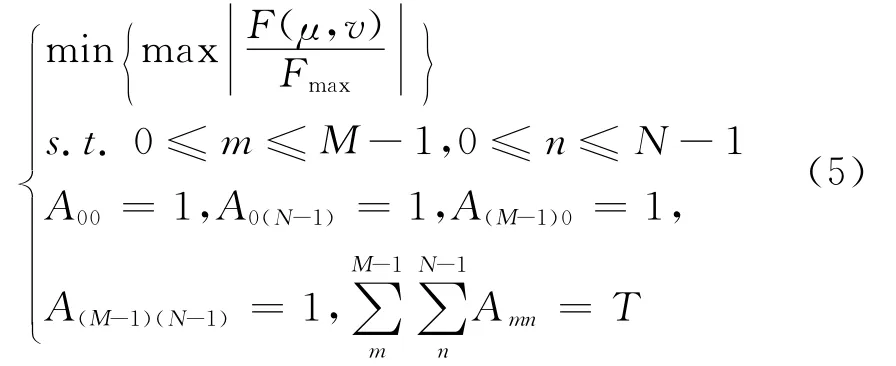
式中：Fmax为主瓣峰值。如果第（m，n）阵元被稀疏，则Amn＝0，否则Amn＝1.这里规定矩形平面阵列的角阵元不能被稀疏。

2 迭代FFT算法

运用迭代FFT算法来实现矩形平面稀疏阵列优化的流程图如图2所示［2]。实验表明，一次迭代循环往往经过4～6次迭代便会结束，每一次迭代循环得到的最优PSL（局部最优PSL）未必能达到给定的旁瓣约束条件，但是制定合理的旁瓣约束条件，就能使局部最优PSL接近给定的旁瓣约束。因此只要进行足够多次迭代循环，每次迭代循环都以一个随机的初始阵元激励矩阵开始，各个迭代循环相互独立，就有很大的概率得到一个最优或近似最优的阵元分布，取局部最优PSL中的最小值作为最后的优化结果。因为运用FFT快速算法计算方向图函数，并且每次迭代循环的迭代次数很少，所以整个优化过程很快就能完成。

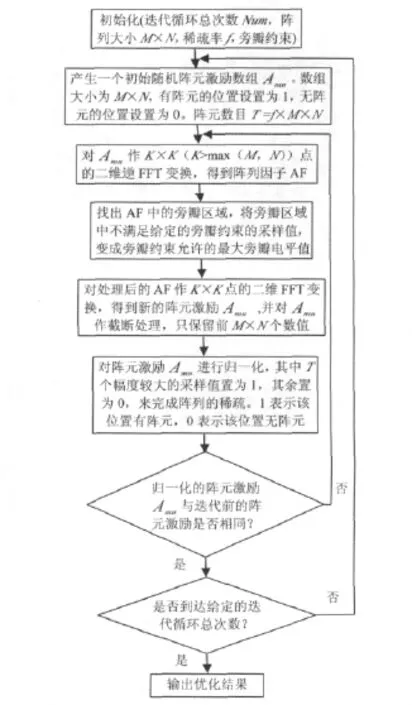
图2 流程图

3 计算机仿真结果

分别给出了对称和非对称矩形平面稀疏阵列的优化结果。仿真参数为：阵列大小为10×20，阵元均为理想的全向性天线单元，栅格间距d＝0.5 λ，二维逆FFT与FFT运算点数K×K＝256×256，迭代循环总次数Num＝1 000次。规定平面稀疏阵列的角阵元不能被稀疏。

3.1 对称矩形平面稀疏阵列优化结果

稀疏率为54%，旁瓣约束为－24.00dB的对称矩形平面稀疏阵列优化结果如图3所示，优化后的PSL为－18.68dB，与文献［3]中对相同阵列大小，相同稀疏率的对称矩形平面稀疏阵列运用遗传算法进行优化，得到的PSL－14.40dB相比改善了4.28dB.其中3（a）图为优化后的阵元位置分布图，白色表示该位置有阵元，黑色表示该位置无阵元，3（b）图为阵列方向图，只取了四分之一象限，3（c）图是其在v＝0和μ＝0时的截平面波束图。

3.2 非对称矩形平面稀疏阵列优化结果

稀疏率为54%，旁瓣约束为－25.00dB的非对称矩形平面稀疏阵列优化结果如图4、图5所示，优化后的PSL为－19.69dB，与3.1节中的对称矩形平面稀疏阵列的优化结果相比改善了1.01 dB.图5是优化过程中，优化效果最好、优化效果最差、迭代次数最少和迭代次数最多的迭代循环中的PSL变化情况，从图中可以看出稀疏阵列的旁瓣性能经过少次迭代后得到了显著的改善。

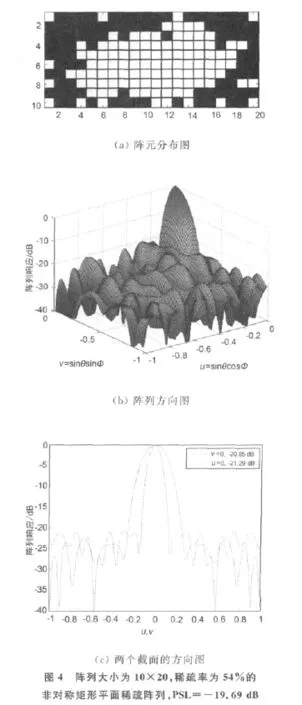
通过对上述仿真结果的观察和比较，可以发现，得到的矩形平面稀疏阵列优化结果是符合阵列优化规律的，即在优化阵列中，阵元的稀疏总是发生在阵列边缘，而阵列中心的阵元一般不会被稀疏掉［4]。并且阵元关于阵列中心非对称分布，增加了可利用的优化自由度，更利于提高稀疏阵列的旁瓣性能［5]。

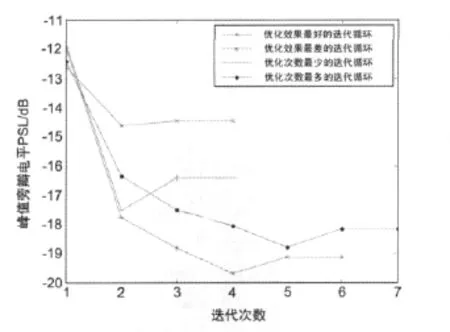
图5 峰值旁瓣电平的收敛情况

3.3 优化方法的性能分析

以上所有仿真均在MATLAB7.1中完成，计算机配置为：AMD Phenom（tm）9650Quad－Core处理器，主频为2.3GHz，每次仿真所花费的时间仅需1min左右。表1给出了阵列大小为10×20，稀疏率为54%，旁瓣约束为－24.00dB的对称矩形平面稀疏阵列20次相对独立的优化结果，其中最好的结果为－18.68dB，最差的结果为－17.84 dB，平均值为－18.08dB，方差为0.028 2.结果表明每次优化得到的PSL总是在一个很小的范围内变化。这说明了该优化方法具有高效性和稳健性。

表1 矩形平面稀疏阵列20次相对独立的优化结果（PSL／dB）

4 结 论

迭代FFT算法在解决稀疏阵列的优化问题上，有其独特的优势。使用迭代FFT算法快速地实现了矩形平面稀疏阵列的优化设计，对解决此类问题提供了有益的启示，为工程运用提供了有价值的参考。仿真结果证明了该方法的高效性和稳健性。此外，该优化方法还可直接应用到大型平面稀疏阵列的优化设计当中。

［1]王玲玲，方大纲.运用遗传算法综合稀疏阵列［J].电子学报，2003，31（12A）：2135－2138.

［2]KEIZER W P M N.Large planar array thinning using iterative FFT techniques［J].IEEE Trans.Antennas and Propagation，2009，57（10）：3359－3362.

［3]HAUP T R L.Thinned arrays using genetic algorithms［J].IEEE Trans.Antennas and Propagation，1994，42（7）：993－999.

［4]陈客松，何子述，韩春林.利用GA实现非对称稀疏线阵旁瓣电平的优化［J].电子与信息学报，2007，29（4）：987－990.

［5]陈客松，何子述，唐海红.对称线阵的优化稀疏研究［J].电子与信息学报，2009，31（6）：1490－1492.

［6]KEIZER W P M N.Linear array thinning using iterative FFT techniques ［J].IEEE Trans.Antennas and Propagation，2008，56（8）：2757－2760.

［7]KUMARUMAR B P，BRANNER G R.Generalized analytical technique for the synthesis of unequally spaced arrays with linear，planar，cylindrical or spherical geometry［J].IEEE Trans.Antennas and Propagation，2005，53（2）：621－634.

［8]CHEN Ke－song，HE Zi－shu，HAN Chun－lin.A modified real GA for the sparse linear array synthesis with multiple constraints［J].IEEE Trans.Antennas and Propagation，2006，54（7）：2169－2173.