基于线性和非线性混合预测的改进连续潮流法

李 林，康积涛

(西南交通大学电气工程学院，四川成都 610031)

连续潮流法是一种基于负荷的变化和发电机的功率分配而追踪电力系统静态行为的一种有效的工具［1－4］。在电力系统静态电压稳定分析中，通常利用连续潮流法绘制PV曲线来反映负荷点的临界电压和极限功率。连续潮流法是通过引入负荷参数采用预估校正技术，在PV曲线的每一点反复迭代，计算出准确的潮流解，它主要由4部分组成:参数化、预测、校正和步长控制。参数化是避免在功率极限处潮流方程的雅各比矩阵奇异，文献［4］、［5］指出弧长参数化比局部参数化更具有鲁棒性;预测是为了找到一个潮流解的近似值，为下一步校正时解潮流方程提供一个初始值，预测值与实际值越接近，校正过程的迭代次数就越少。文献［6］通过对潮流方程的变换，摆脱了对负荷参数的依赖，改善了连续潮流法的收敛性，由于其预测环节仍要解线性方程组，降低了计算的效率;文献［7］采用非线性拉格朗日插值法预测，在PV曲线功率极限处可以采取较大步长，减少计算时间，但是在PV曲线下半支部分其预测解与实际解的接近程度不太理想。

为了提高计算效率，提出了基于线性和非线性混合预测的改进算法。该算法在PV曲线上半支和下半支的功率极限附近采用非线性预测，剩下部分采用割线预测。该方法在IEEE 39节点系统中和其他方法作了比较，体现了其有效性和快速性。

1 连续潮流法说明

1.1 电力系统潮流方程

一般地，在静态输电计算中，极坐标系统下的潮流方程可用式(1)表示为

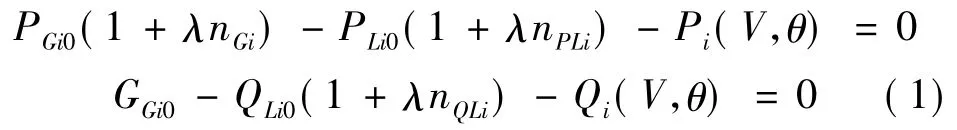
式中，λ表示发电机和负荷的增长参数，即为负荷因子;nGi、nPLi分别表示发电机和负荷有功、无功增长的方向向量;PGi0、QGi0为节点的发电机出力;PLi0、QLi0为节点 i的负荷;Pi(V，θ)、Qi(V，θ)分别表示节点的有功和无功，其具体表达式如下。

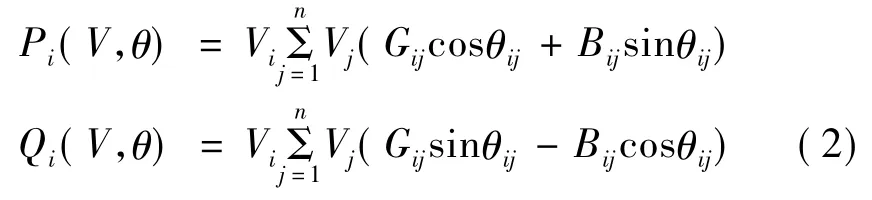
其中，Vi是节点的电压幅值;θij是节点i和节点j的电压相角差值;Gij、Bij为节点i与节点j之间的网络导纳矩阵的实部和虚部。

1.2 非线性预测

非线性预测方法主要由一个多项式函数逼近PV曲线上已知解，当多项式函数确定后，对于一个给定的步长，下一个解则可以利用外推技术来预测。如图1所示，通过3个潮流实际解1、2、3，利用非线性预测得到预估解4。最常用的多项式逼近方法是拉格朗日插值法。

图1 非线性预测示意图

根据已知的实际潮流解，预估解就可以由拉格朗日多项式插值的多项式逼近获得。拉格朗日多项式可以由式(3)给出。

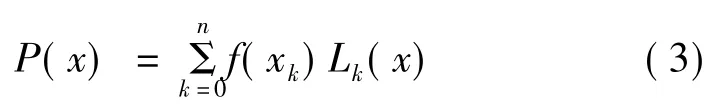
其中，P(x)为拉格朗日插值多项式;xk为已知的潮流解;Lk(x)为拉格朗日插值系数;n为多项式的阶数。若已知n+1个点，则拉格朗日插值系数表示如下。

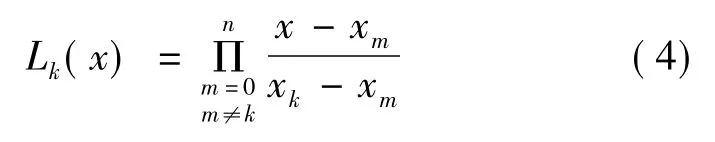
由于电力系统PV曲线近似二次函数，通常预估值通过拉格朗日二次插值多项式获得［7］。

给定一个弧长sj+1，由式(3)能求出第j+1步的预估值。例如，图1中已知3个潮流解(s1，x(s1))、(s2，x(s2))、(s3，x(s3))，可以通过拉格朗日二次插值多项式来估计第4个潮流解()。取一个适当的步长△s，则

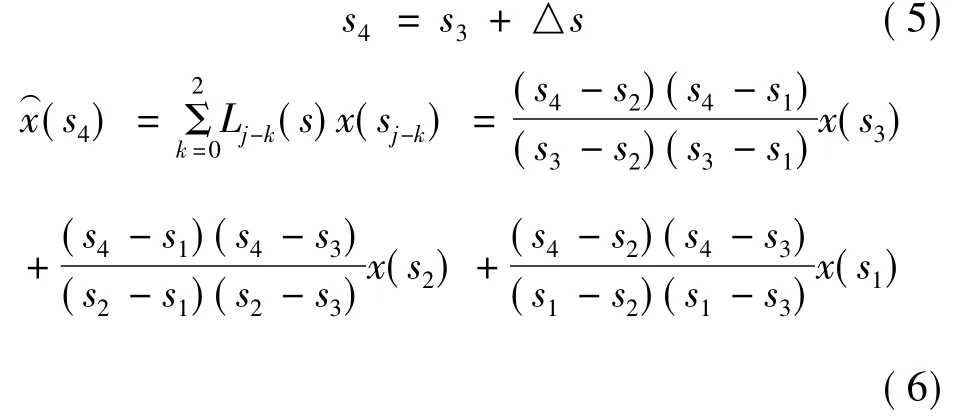
1.3 已有的非线性预测算法说明

采用拉格朗日非线性方法预测，在PV曲线功率极限处可以采用较大的步长加快计算速率，然而研究表明非线性预测对于PV曲线的下半支部分并不是有效，因为非线性应用的是弧长与状态变量的关系。如图2所示，可观察出曲线是关于A点对称的，而实际系统中很多节点的电压幅值与PV曲线下半支弧长的关系不同于与上半支弧长的关系。

图2 弧长和状态变量的关系图

2 改进的连续潮流法

针对以前方法的不足做了如下改进:把PV曲线分为两个区域，如图3所示。区域Ⅰ为PV曲线上半支和下半支的功率极限附近，由于非线性预测具有较好的鲁棒性和非线性，并且弧长与PV曲线的上半支有近似二次函数的关系，因此采用二阶拉格朗日插值法预测具有较高的精度和速度。区域Ⅱ为PV曲线剩下部分，利用割线法预估，避免了第2.3中说明的非线性预测的问题。区域Ⅰ向区域Ⅱ过渡时，由阈值β控制。当在曲线下半支|△x/△λ|≤β时，区域Ⅰ向区域Ⅱ过渡。

图3 PV曲线区域图

步长控制是连续潮流法中的一个关键环节，步长过小将造成预估校正步数太多，步长过大将使得校正过程收敛缓慢甚至发散。理想的情况下是，步长应该随着曲线的曲率大小进行自适应调节:潮流解曲线在曲率小的部分，即平坦部分采用较大的步长，在曲率大的部分采用较小的步长。这里利用曲线上紧挨着的两点(xj，λj)和(xj－1，λj－1)来控制步长，其表达式为

式中，MAX=max(|Vj－Vj－1|)，其中 V 为状态变量中x节点电压的幅值;a、b是系数。从式(7)中可以看出，曲线在曲率小的部分，电压幅值变化较大，此时步长取值较小;在曲率大的部分，电压幅值变化较小，步长取值较大，这样步长的大小就根据曲线曲率的大小自动变化。

3 算例分析

用IEEE 39节点测试系统对改进的连续潮流法进行了效率评估。所有仿真没有考虑发电机无功限制，所有的负荷和发电机的有功和无功按同一比例增长，负荷为恒功率模型，并且保持功率因数不变。

为了方便，把方法定义如下。

方法A:切线法;

方法B:非线性法;

方法C:改进方法，步长控制采用式(7)，在区域Ⅰ中采用非线性拉格朗日插值法时，式中a、b分别取0.5和2.5;在区域Ⅱ中采用割线法时，式中a、b分别取0.4和3;区域Ⅰ向区域Ⅱ过渡时的阈值β取1.12。

图4 IEEE 39节点母线12的PV曲线图

图4 显示了IEEE 39节点系统在节点31的PV曲线，图中(a)、(b)、(c)分别表示用方法 A、B、C 绘制的PV曲线。从图中可以观察出，在PV曲线的功率极限处C方法和D方法所得的预估点与相应的校正点非常接近，说明利用非线性预测曲线曲率大的部分具有很好的鲁棒性。

表1比较了A、B、C 3种方法CPU的计算时间，其中RA、RB分别表示了其他方法相对于A、B方法CPU计算时间的比率。从表中可以看出方法C相对于方法A、B分别减少了CPU时间的35.7%、6.5%。图5显示了绘制曲线每步所需要的迭代次数，从图中可以看出A、B、C 3种方法绘制曲线的步数分别为22、21、20步;采用了非线性预测法的B、C方法在曲线极限功率处的迭代次数最多达3次，在曲线的下半支仍采用B方法导致迭代次数增加，达到了5次，这就是由于曲线在下半支的弧长与状态变量的关系不同于上半支弧长与状态变量的关系。

表1 IEEE 39节点系统CPU时间比较

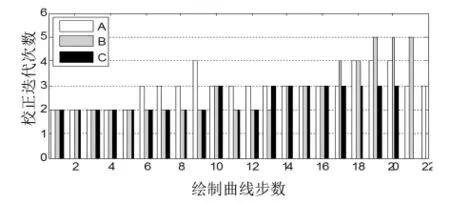
图5 绘制曲线步数和校正迭代次数关系图

4 结论

对求解PV曲线的连续潮流法进行了改进。通过线性和非线性的混合预测，解决了常规非线性预测在PV曲线下半支的问题，有效地改善了连续潮流法的性能。采用自动变步长提高了程序的效率。通过IEEE 39节点测试系统的算例分析，表明了该方法的正确性和有效性。

［1]Okumura k.，Terai k.，Kishima A..Solution of Ill－ conditioned Load Flow Equation by Homotopy Continuation method［J］.Circuits and Systems.IEEE International Sympoisum，1991(5):2897－2899.

［2]Ajjarapu V.，Christy C.The Continuation Power Flow:a Tool for Steady State Voltage Stability Analysis［J］.IEEE Transactions on Power Systems，1992，7(1):416 －423.

［3]Canizares C.A.，Alvarado F.L..Point of Collapse and Continuation Methods for Large ac/dc Systems［J］.IEEE Transactions on Power Systems，1993，8(1):1 －8.

［4]H.D.Chiang，A.J.Flueck，K.S.Shah，N.Balu.CPFLOW:A Practical Tool for Tracing Power System Steady－state Stationary Behavior Due to Load and Generation Variations［J］.IEEE Transactions on Power Systems，1995，10(2):623 －634

［5]S.H.Li，H.D.Chiang.Nonlinear Predictors and Hybrid Corrector for Fast Continuation Power Flow［J］.IET Generation，Transmission Distribution，2008，2(3):341 －345.

［6]蔡伟程，代静.对求取电力系统PV曲线的连续潮流法的改进［J］.电力系统及其自动化学报，2005，17(5):82－85.

［7]Mori H.，Yamada S..Continuation Power Flow with the Nonlinear Predictor of the Lagrange’s Polynomial Interpolation Formula［J］.Transmission and Distribution Conference and Exhibition 2002:Asia Pacific，IEEE/PES，2:1133－1138.