一类带强迫项的脉冲多时滞微分方程的振动准则

2012-07-16孙琳王利兵顾长超

五邑大学学报（自然科学版） 2012年3期

关键词：四阶时滞准则

孙琳，王利兵，顾长超

孙琳1，王利兵2，顾长超1

（1.安徽大学数学科学学院，安徽合肥 230039；2. 重庆理工大学数学与统计学院，重庆 400054）

对一类四阶带强迫项的脉冲多时滞微分方程的解的振动性作了研究，给出引理解决了方程的非振动解与其各阶导数的符号关系，得到其振动性的判别准则.

脉冲微分方程；多时滞微分方程；强迫项；振动性

脉冲现象在现代科技各个领域的实际问题中普遍存在，其数学模型往往可归纳为脉冲微分系统. 近年来，对脉冲微分方程的研究非常活跃，除了在数学本身方面的应用，脉冲微分方程还为刻画物理、生物、工程等领域中的许多现象提供了有效的研究工具和可行的研究方法. 以前文献对二阶脉冲微分方程的振动性的研究较多[1-3]，但对四阶脉冲微分方程的振动性研究较少. 本文对一类四阶带强迫项的脉冲多时滞微分方程进行了研究，在文献[4]的基础上推导出该方程的解的振动性，得到了其振动性的判别准则.

本文主要考虑如下脉冲时滞微分方程：

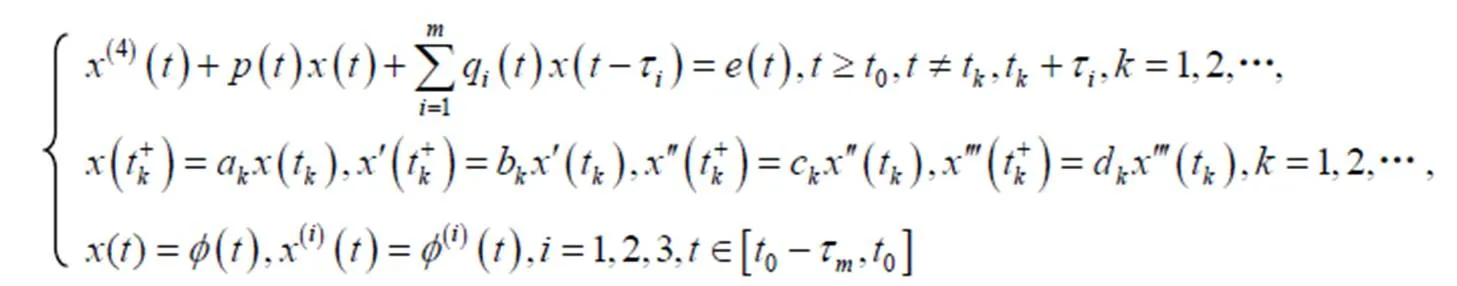
本文总假设下面条件是成立的：

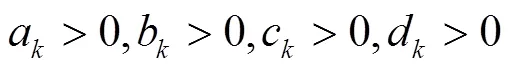
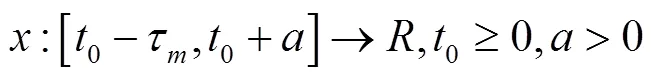
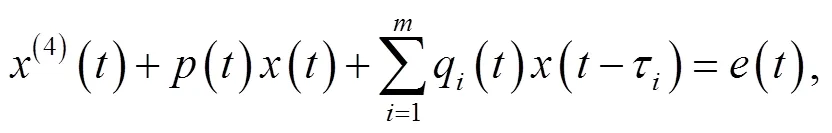
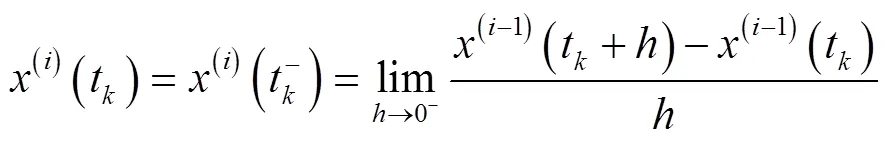
定义2[6]如果系统（1）的解最终为正或最终为负，则称这个解为非振动的；否则，称该解为振动的. 如果系统（1）的所有解均为振动的，则称系统（1）为振动的.

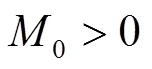
由于系统（1）可转化为一阶脉冲时滞微分方程组，文献[8]已经讨论了系统（1）的解的整体存在性. 以下总假设系统（1）的解是整体存在的.

1 主要结论

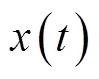
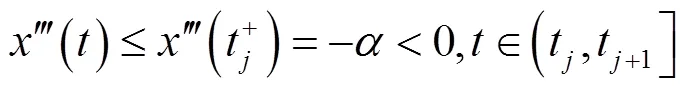
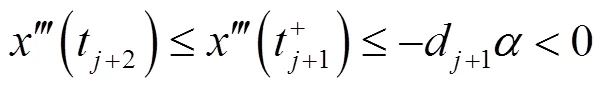
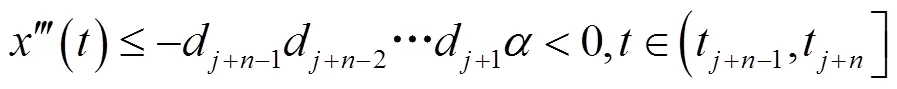
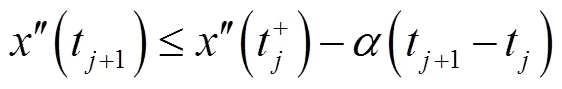
由式（3）和式（5），类似可得

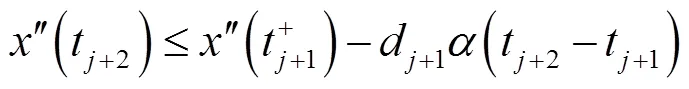
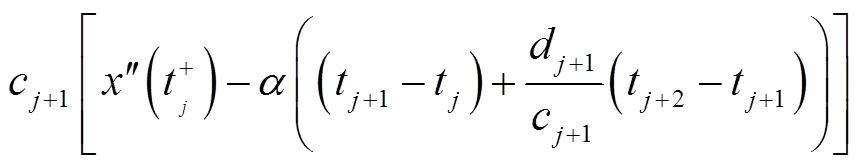
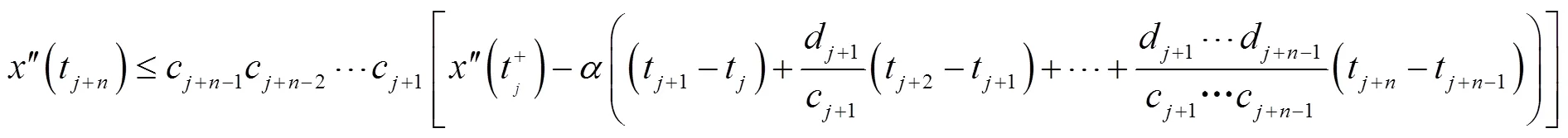
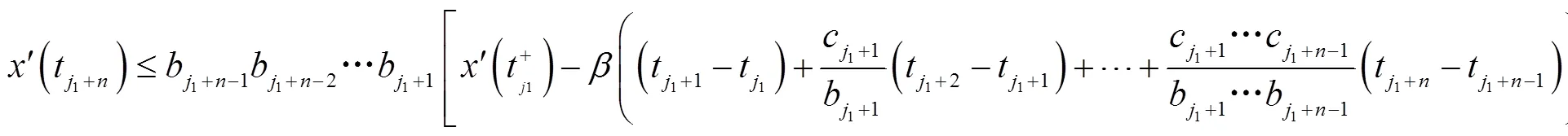
综合i）和ii）即可. 证毕.

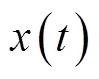
定理4[10]509-510假设引理1中条件1～3成立，若还有

则系统（1）的任意有界解是振动的.

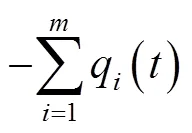
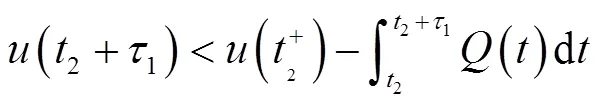
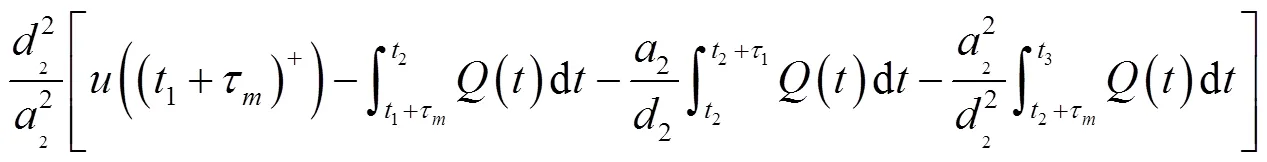
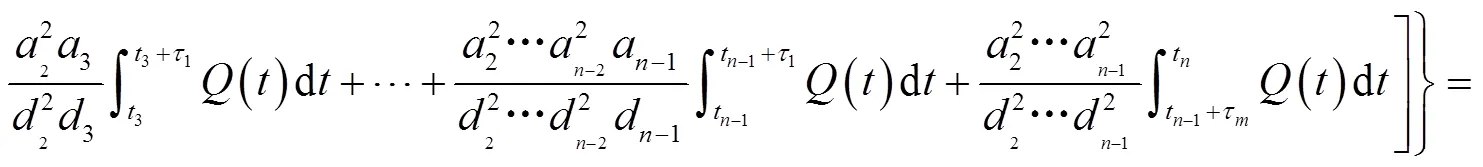
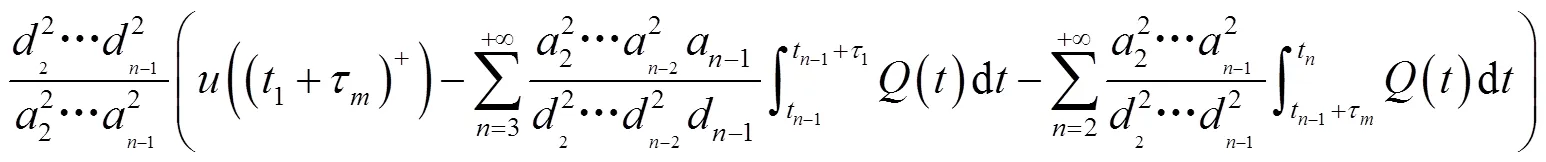
同理可得，

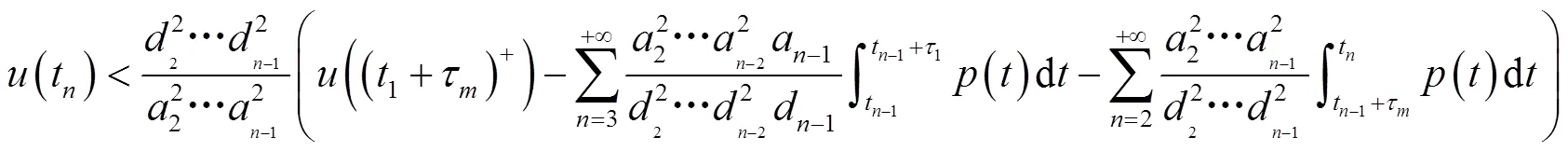
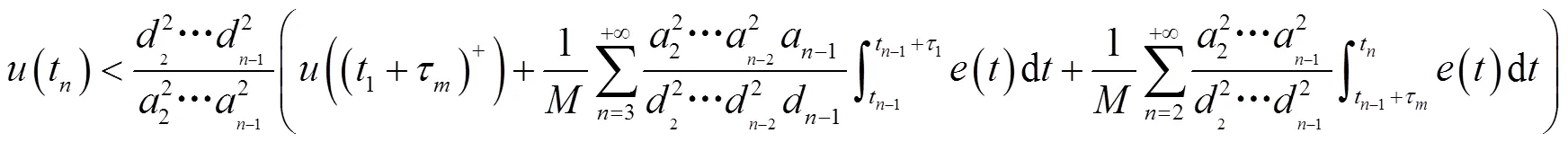
[1] SHEN Jianhua. Qualitative properties of solution second-order linear ODE with impulses[J]. Math Comp Model, 2004, 40(3-4): 337-344.

[2] 黄木根，冯伟贞. 带强迫项的二阶脉冲时滞微分方程的振动性[J]. 黑龙江大学学报：自然科学版，2006, 23(4): 452-456.

[3] LUO Jiaowan. Second-order quasilinear oscillation with impulses[J]. Computers and Mathematics with Applications, 2003, 46 (2-3): 279-291.

[4] 叶国炳，申建华. 带强迫项的阶脉冲微分方程的振动性与渐近性[J]. 系统科学与数学，2010, 30(4): 501-514.

[5] 林丹玲. 偶数阶中立型时滞微分方程的振动性[J]. 五邑大学学报：自然科学版，2010, 24(2): 46-51.

[6] 杨甲山，张晓建. 具正负系数的二阶阻尼微分方程的振动性[J]. 高校应用数学学报，2011, 26(4): 399-406.

[7] 毛卫华，万安华. 三阶脉冲时滞微分方程解的振动性与渐近性[J]. 兰州理工大学学报，2005, 31(2): 130-133.

[8] LAKSHMIKANTHAM V, BAINOV D D, SIMEONOV P S. Theory of impulsive differential equations[M]. Singapore: World Scientific, 1989: 32-33.

[9] 叶国炳，周小奇，李世国. 带阻尼项的三阶脉冲微分方程的振动性与渐近性[J]. 数学的实践与认识，2011,1 41(1): 153-158.

[10] 林敏，刘演军. 高阶脉冲时滞微分方程解的振动准则[J]. 数学理论与应用，2010, 30(4): 1-5.

Oscillation Criteria for a Class of Impulse and Multiple Delay Differential Equations with Forcing Terms

SUNLin1, WANGLi-bing2, GUChang-chao1

(1. School of Mathematical Sciences, Anhui University, Hefei 230039, China; 2. School of Mathematics and Statistics, Chongqing University of Technology, Chongqing 400054, China)

The paper focuses on the oscillations of a class of fourth-order impulse and multiple delay differential equations with forcing term. A lemma is given to deal with the sign relation of the non-oscillatory solutions and the derived functions. Some criterions about the oscillation of the solutions to the equations are obtained.

impulsive differential equations; multiple delay differential equations; forcing terms; oscillation

1006-7302（2012）03-0018-05

O175.1

2012-04-20

教育部博士点基金资助项目（20113401110001）

孙琳（1987—），男，安徽无为人，在读硕士生，研究方向为微分方程.