单位线的发展及启示
2012-07-14芮孝芳刘宁宁
芮孝芳,刘宁宁,凌 哲,梁 霄
(河海大学水文水资源学院,江苏南京 210098)
1 单位线的起源
在经济社会不发达的古代,人类在防治洪水灾害时,首先直觉关注的是河道某断面出现的洪峰水位和洪峰流量。因此,早在19世纪人们就有了如何由暴雨确定所形成的洪峰流量的愿望。Mulvany于1850年提出了水文学历史上第一个由暴雨计算所形成的洪峰流量的公式[1],后人称之为合理化公式。随着经济社会的发展,人们对防治洪水灾害的要求也不断提高,逐步认识到了解一场暴雨所形成的流域出口断面洪水过程比仅了解洪峰水位和洪峰流量更为重要、更为全面。但流域由坡面和水系组成,坡面上的水流现象要比河道中水流现象复杂得多,以致于适用于河道水流的理论和计算方法,一般并不能直接用于坡面水流计算。因此,尽管早在1871年就有了圣维南根据牛顿力学定律导出的描写河道洪水波运动的明渠缓变不稳定偏微分方程组,但如何由暴雨过程计算流域洪水过程的问题仍没有得到解决。
直到20世纪二三十年代,情况才有了转机。这一时期是水文学蓬勃发展时期,新的水文学理论和方法不断涌现,仅为了解决流域上一场暴雨形成的洪水过程的计算问题就提出了两种方法:一是Ross于1921年提出的时间-面积曲线概念,据此建立的方法称为等流时线法;二是Sherman于1932年提出的单位线概念,据此建立的方法称为Sherman单位线法。等流时线法设想在流域上存在等流时线,降落在同一条等流时线上的雨滴经过相同的汇流时间将同时刻到达流域出口断面。这样,只要找出了流域的等流时线,就可完成由流域上一场暴雨过程推求其形成的流域出口断面洪水过程的计算任务。单位线法是先定义一条流域单位线。所谓单位线就是指流域上分布均匀的单位时段内强度不变的1个单位的净雨量所形成的流域出口断面流量过程。应用这条单位线处理流域出口断面洪水过程计算的基本思路是:如果单位时段内强度不变的净雨量不是1个单位,而是n个单位,那么其所形成的流域出口断面的洪水过程为单位线的 n倍,这叫做倍比性假设。如果一场暴雨的历时不只是1个单位时段,而是有m个单位时段,那么其所形成的流域出口断面洪水过程就是各个单位时段净雨形成的流域出口断面洪水过程之同时刻流量之和,这叫做叠加性假设。因此,只要找到了流域单位线,就可以根据倍比性和叠加性假设,完成推求流域上一场暴雨所形成的流域出口断面洪水过程的计算任务。
与Sherman直接针对实际应用提出单位线不同,美国Boston土木工程协会早于Sherman两年即1930年,提出了“瞬时暴雨产生的过程能表征流域特征”的概念[2],这种所谓“瞬时暴雨产生的过程”就是后人命名的“瞬时单位线”。但它并没有立即得到应用,直到1945年,Clark才据此概念求得单位线用于流域汇流计算[3]。对瞬时单位线的解释最初只是认为:“时段长为零的单位线就是瞬时单位线”,直到20世纪70年代才将瞬时单位线正式定义为:流域上分布均匀,历时极短(→0),强度极大(→∞),但总量为1个单位的净雨所形成的出口断面流量过程。
在不断发展的近代科学技术支撑下,水文学家现在终于搞清楚了Sherman单位线的3个基本假设实质上就是认为流域汇流遵循倍比性和叠加性[1,4]。现在已经证明,自然界一切可以用线性微分方程或线性系统描写的物理过程都满足倍比性和叠加性,而且,一旦满足了倍比性和叠加性这一前提,时段长为0时的单位线就成为瞬时单位线;反之,瞬时单位线对时段的积分就成为单位线[5-6]。现在,瞬时单位线已成为单位线法的核心问题,而且在洪水演算中也得到了应用。
由于在许多情况下Sherman提出的单位线和Clark首次使用的瞬时单位线都能获得令人满意的计算效果,且既简单又方便,因此,在世界各国得到了广泛的应用。单位线法并非来自直接的实验发现,而是来自科学家对降雨形成流域出口洪水过程的一种理性思维。为什么在实用中对多数情况都能取得令人满意的效果呢?这种先有“方法”后有“理论”的发展过程很耐人寻味,引起了水文学家的重视和极大的兴趣,单位线方法从此走上了一条蓬勃发展之路。
2 单位线的系统论解释
曾经对水文科学作出重大贡献的Chow早在20世纪60年代就认为流域汇流可作为一个用下列线性动力系统微分方程来描述的系统[7]:

式中:Q(t)为出口断面流量过程;h(t)为相应于出口断面流量过程的净雨过程;a0,a1,…,am,b0,b1,…,bn均为常数或者仅是时间t的函数。
根据瞬时单位线的定义,如果净雨输入为 δ函数,那么所形成的流域出口断面流量过程就是流域瞬时单位线u(t)了。这时式(1)将变成

对式(2)的两边进行Laplace变换,得式中:p为Laplace变换的参量。

考虑到L[δ(t)]=1,并对式(3)求逆 Laplace变换,得
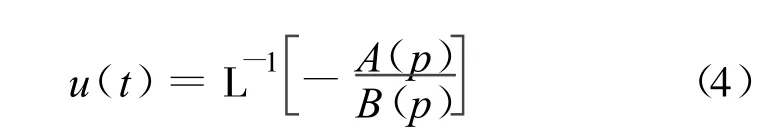
式(4)就是流域瞬时单位线的系统论释义。由此可见,流域瞬时单位线反映了系统的作用,因而与流域的地形地貌特性有关。
如果直接对式(1)进行求解,那么根据运算微积分中的有关定理,可得
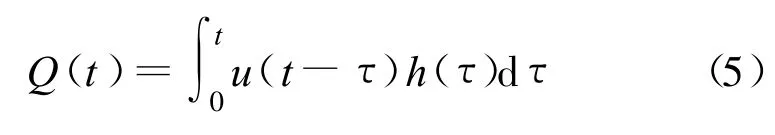
表达Q(t),u(t)和h(t)之间关系的式(5)称为卷积分,因为它首先由Duhmanmel得到,所以又称Duhmanmel积分[5],其中被积函数为两个函数的乘积,体现了线性系统的倍比性,而从0到t的积分体现了线性系统的叠加性。
3 单位线的物理学解释
如果净雨是在 τ时刻呈空间分布均匀状态瞬时注入流域的,且由 n个水滴组成,那么均匀分布在流域上的n个水滴都是从τ时刻开始从流域上不同位置向流域出口断面汇集的。由于每个水滴的流域汇流时间不一样,所以,τ时刻注入的n个水滴必将在不同时刻到达流域出口断面,显然,只有那些流域汇流时间正好等于 t-τ的水滴能在t时刻到达出口断面,从而组成了 t时刻的流域出口断面流量[6]。如果把满足这个条件的水滴所占据的面积计算出来,并用表示,那么这个面积与 τ时刻降雨强度i(τ)的乘积,就是 τ时刻净雨对t时刻流域出口断面流量的贡献,即

一场降雨由连续时刻的降雨组成,把一场降雨中每一个时刻净雨对 t时刻出口断面流量的贡献都计算出来,就可得到t时刻出口断面的流量

如果入流和出流均采用m3/s作单位,那么式(7)又可写成:
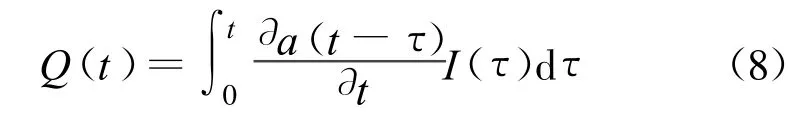
式(8)称为径流成因公式。将式(8)与式(5)进行比较,不难得知式(8)中的即为流域汇流的瞬时单位线,这就把流域瞬时单位线的物理意义揭示出来了。
4 单位线的概率论解释
笔者[8]认为,大气中凝结成的水滴何时以降雨的形式降落到流域表面,可视为一随机事件,即雨滴降落的时间S就是随机变量。因此,将净雨强度过程h(t)作归一化处理,就成为雨滴降落时间S这一随机变量的分布密度,用fh(s)表示:

降落在流域表面的净雨滴,经由坡地汇流和河网汇流将成为流域出口断面的流量过程。降落在流域表面的净雨滴何时到达流域出口断面也可视作一随机事件,即雨滴到达流域出口断面的时间T也是随机变量。因此,将流域出口断面流量过程Q(t)作归一化处理,就成为随机变量净雨滴在流域出口断面出现时间T这一随机变量的分布密度,用 fQ(t)表示:

因为净雨滴降落到流域表面的时间为S,所以,如果净雨滴从其在流域上的注入点流达流域出口断面的汇流时间为 Σ,那么净雨滴从降落至流域表面开始,最终在流域出口断面出现的时间T应为

前已分别给出随机变量S和T的分布密度为fh(s)和fQ(t),如果用fB(t)表示净雨滴流域汇流时间 Σ的分布密度,并假设S与Σ相互独立,那么根据概率论中随机变数函数的分布理论[9],由式(11)可导得:

或

将式(9)和式(10)代入式(12),并考虑流域汇流阶段的水量平衡关系,得

或

比较式(13)和式(5),可见式(13)不仅是式(5)的概率论诠释,而且流域瞬时单位线u(t)就是净雨滴流域汇流时间的分布密度fB(t),即

式(14)与 Rodriguez-Iturbe等[10]于 1979年基于粒子弱相互作用下随机运动理论和流域水量平衡原理导得的结果完全一致。
5 综合单位线
1938年,Snyder在研究美国Appalachian山地的暴雨径流时,为解决缺乏水文资料情况下Sherman单位线的确定问题,通过分析Sherman单位线的特征值,如单位线峰值、单位线洪峰滞时、单位线总历时等与地形地貌参数,如流域面积、主河道长度、流域中心至流域出口断面距离LC等之间的关系,建立了相应的经验公式[11]。1960年,Nash为了将其创建的Nash瞬时单位线应用于缺乏水文资料流域的流域汇流计算,针对英国资料,建立了其中参数 n和k与地形地貌之间的经验公式[12]。此后,Rosso又从另外的角度得到了Nash模型参数与Horton地貌参数之间的经验性关系[13]。1978年,Body在寻求概念性模型参数与地形地貌参数定量关系的研究中也做出了一些富有启发性的工作[14]。这种由经验公式求得的单位线就称为综合单位线。
无论是Snyder还是Nash以及其他后来者,在建立综合单位线时都是采用统计综合途径。统计综合途径的基本思想是[15]:通过对水文过程和地貌过程相互作用的观测和分析,寻找出影响水文过程特征的地形地貌参数,利用积累的观测或实验资料建立两者的定量关系,或者通过对水文过程进行宏观考量,构建能模拟水文过程的概念性水文模型,进而建立这类模型参数与地形地貌参数的定量关系。这种建立水文过程与地形地貌参数定量关系的途径,通常有两种具体实施方法:一是先给定两者之间的函数形式,然后确定其中的参数;二是采用某种模拟仿真计算,以隐式方式直接拟合两者关系,而无须事先给定它们之间的函数形式。属于前者的主要有统计回归分析和最优化方法;属于后者的主要有人工神经网络算法等。
由于统计综合途径只是从影响因素分析上,而不是从物理机制上探讨水文过程与地貌过程的定量关系,因此其对水文气象资料观测的依赖性较大,没有足够数量的水文气象观测资料是难以得出有价值的分析成果的。在应用中,对其外延和移用也应十分慎重。
6 地貌瞬时单位线
6.1 R-V地貌瞬时单位线
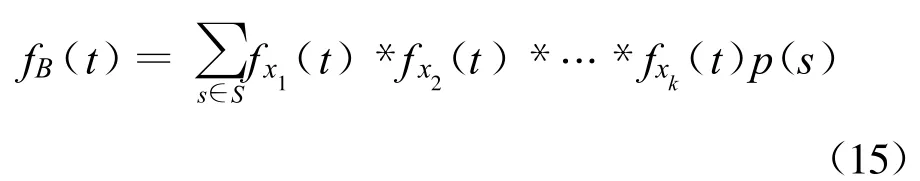
1979年,Rodriguez-Iturbe等[10]基于式(14),应用概率论、水系地貌结构理论和水文学原理由Rodriguez-Iturbe等导出了如下流域瞬时单位线的表达式:式中:s为“水滴”到达出口断面的状态路径;x1,x2,…,xk为组成该s的状态,分别在各级河流状态和各级坡地状态中选择;fx1(t),fx2(t),…,fxk(t)为“水滴”在状态 x1,x2,…,xk中持留时间的概率密度;p(s)为“水滴”选择s的概率;S为s的集合。
式(15)中之p(s)可由Horton地貌参数确定,fxk(t)(k=1,2,…)可由“水滴”通过状态 xk(k=1,2,…)的动力因子确定。
由于在式(15)的具体表达式中包含有地形地貌参数,故称所得到的瞬时单位线为地貌瞬时单位线。
6.2 概率组合地貌瞬时单位线

呈均匀分布并瞬时降落在流域上的无穷多雨滴中的任一个,总是要以一定的运动速度V通过L长的路径到达流域出口断面的,因此,其流域汇流时间T必为由于任一雨滴什么时间降落到流域可视为随机的,因此其运动速度V和所取的路径长度L均为随机变量,而且L和V是相对独立的。根据概率论中随机变量函数的分布的理论,式(16)中3个随机变量的分布密度应有如下关系[16]:式中:g(l)和 φ(v)分别为随机变量的分布密度;vmax为流域中净雨滴的最大运动速度。

式(17)表明,只要能得到 g(l)和 φ(v),就可按此式推求流域瞬时单位线了。文献[16]认为,g(l)可由宽度函数给出,φ(v)可通过坡度的分布密度求得。因为宽度函数和坡度分布密度表达的均为流域地形地貌特征,所以由式(17)求得的瞬时单位线也属于地貌瞬时单位线。
国外发表类似的研究成果比笔者的工作晚了3年[17]。
7 一些启示
单位线来自水文学家急切解决流域降雨形成出口断面流量过程问题的强烈愿望,也是水文学家处理复杂的、特殊的流域汇流现象的一种灵感,而倍比性和叠加性假设则起到了“桥”的关键作用。单位线的成功应用及较好的普适性,说明了用倍比性和叠加性架起的“桥”虽系“假设”,但已不自觉地切中了流域汇流现象的本质,符合了在许多情况下,净雨水滴从流域各处向出口断面汇集遵循倍比性和叠加性的客观事实。
在线性条件下,流域单位线或瞬时单位线的唯一性就意味着净雨空间分布必须均匀。如果净雨空间分布不均匀,那么流域单位线或瞬时单位线就不可能唯一。事实上,暴雨中心在上游和下游,所得出的流域单位线或瞬时单位线必然会有较大差别。因此,在给出流域单位线或瞬时单位线的定义时,绝对不可以漏掉“净雨空间分布均匀”这一重要前提。而在实际应用中,原则上也必须要求净雨在流域上呈均匀分布。以往曾经有人提出应按暴雨中心位置率定单位线和使用单位线的问题,这实际上并不妥当,理论上也不可取。因为相同降雨量的暴雨,空间分布是不尽相同的,再者暴雨中心位置的量化也是一件十分困难的事。为了满足使用单位线的条件,笔者认为不应是按暴雨中心位置给出单位线,而是应对使用单位线的流域面积大小进行限制,采用划分单元流域或子流域的方法,使净雨在单元流域或子流域上的空间分布尽可能均匀。
瞬时单位线概念的建立是单位线在理论上的重大提升。由于瞬时单位线不受时段长短的影响,它必然综合反映了流域汇流特性,主要考虑了下垫面条件及其空间分布对流域汇流的影响。从物理学和概率论所作的揭示表明,流域瞬时单位线实质上就是均匀分布降落在流域上的无穷个净雨水滴汇集至流域出口断面所形成的时间-面积曲线或汇流时间概率密度,首先对此作出贡献的水文学家是Rodriguez-Iturbe[10],他原本学习理论物理,在攻读博士学位时毅然选择了水文学。所以,单位线理论的提升是水文学中通过学科交叉获得成功的范例之一。
单位线法与等流时线法是差不多同时代展现在世人面前、可用于处理流域汇流的两个方法。表面上看它们似存在差别,但深究起来却发现两者本质上是一致的。如果在单位线的物理学解释上,假设水滴的运动速度为常数,那么等流时面积分配曲线就是单位线了。如果将单位线的物理学解释植入单位线的系统论解释,那么单位线的纵坐标值就是净雨空间分布均匀条件下汇流时间处于该时段内的水滴占全部水滴的比重,也即水滴运动速度相同情况下与该时段相应的等流时面积占全流域面积之比重。可见,在一定条件下,单位线法与等流时线法是可以互相转换的。这就不难发现人们早先对这两个方法优缺点评论的物理本质了。之所以单位线法的优点是考虑了流域调蓄作用,而缺点是只适用于降雨空间分布均匀的情况,就是因为它是针对流域整体,而不必限定水滴运动速度相同。之所以等流时线法的优点是能适应降雨空间分布不均匀的情况,而缺点是不能考虑由于水滴运动速度不同而导致的流域调蓄作用,就是因为它要求水滴运动速度相同,但不必将流域作为一个整体。笔者提出的“基于网格水滴流域汇流计算方法”[18]就是一种吸取单位线法和等流时线法之优点,同时又能排除两者之缺点的汇流计算方法。
[1]DOOGE J C I.Linear theory of hydrologic systems[M].Washington D.C.:USDA,1973.
[2]CHOW V T.Handbook of applied hydrology[M].New York:McGraw-Hill,1964.
[3]CLARK CO.Storage and the unit hydrograph[J].Transactions of the American Society of Civil Engineers,1945,110:1419-1446.
[4]JOHNSTONE D,CROSS W P.Elements of applied hydrology[M].New York:Ronald Press,1949.
[5]芮孝芳.线性时不变汇流系统的初步研究[J].华东水利学院学报,1982(2):63-73.
[6]芮孝芳.水文学原理[M].北京:中国水利水电出版社,2004:275-282.
[7]CHOW V T,KULANDAISWAMY V C.General hydrologic system model[J].Journal of the Hydraulics Division,ASCE,1971,97(HY6):791-804.
[8]芮孝芳.流域汇流机理的概率论体系探讨[J].水科学进展,1999,10(1):20-24.
[9]复旦大学数学系.概率论与数理统计[M].上海:上海科学技术出版社,1960:78-91.
[10]RODRIGUEZ-ITURBE I,VALDES J B.The Geomorphologic structure of hydrological Response[J].Water Resources Research,1979,16(6):1409-1420.
[11]LINSLEY R K,KOHLER M A,PAULHUS J L H.Hydrology for Engineers[M].New York:McGraw-Hill,1982:223-225.
[12]NASH J E.A unit hydrograph study,with particular reference to British catchments[J].Proceedings of the Institution of Civil Engineers,1960,17:249-282.
[13]ROSSO R.Nash model relation to Horton order ratios[J].Water Resources Research,1984,20(7):914-920.
[14]BOYD M J.A storage-routing model relation drainage basin hydrology and geomorphology[J].Water Resources Research,1978,15(6):921-928.
[15]芮孝芳,蒋成煜.流域水文与地貌特征关系研究的回顾与展望[J].水科学进展,2010,21(4):444-445.
[16]芮孝芳.由流路长度分布律和坡度分布律确定地貌瞬时单位线的研究[J].水科学进展,2003,14(5):602-606.
[17]FLEURANT C,KARTIWA B,ROLAND B.Analytical model for a geomorphological instantaneous unit hydrograph[J].Hydrological Processes,2006,20:3879-3895.
[18]RUI Xiao-fang,YU Mei,LIU Fang-gui,et al.Calculation of watershed flow concentration based on the grid drop concept[J].Water Science and Engineering,2008,1(1):1-9.
