基于神经网络的GSM无源探测系统目标检测算法

张平川，杨 洋，高 倩，张超英，谷广超，轩克辉

（漯河职业技术学院 河南 漯河 462002）

无源雷达[1]是一种新体制系统雷达，它本身不发射任何辐射信号而是借助其它电磁波辐射源作为探测照射源获取目标反射信号，所以具有低截获概率的特性。并且对敌方隐形飞机、反辐射导弹、低空突袭等具有较强的优势和生存能力，因此无源探测在现代电子战中具有很重要的意义。基于GSM基站信号的无源雷达相比于其他民用照射源[2-3]如AM，FM，GPS，DBTV，TV，Satellite等，由于基站分布广泛而具有可靠性高的优势[4-6]。GSM无源雷达中，各类杂波直接影响着目标信号的检测，采用一般的卡尔曼滤波等检测效果存在速度慢恒虚警率高的不足，为此文中利用神经网络算法实现对GSM无源雷达目标数据的分析，先用专门研制的相控阵列接收设备接收某个蜂窝探测区域内的目标反射回波，再下变频处理及ICS554采样完成ADC，然后将数据经后验感知的神经网络算法进行处理，从杂波噪声背景下有效分析运动目标的航迹信息，实现目标的探测跟踪。

1 GSM无源雷达系统结构

基于神经网络的GSM无源雷达系统结构如图1所示。图1中每个无源探测系统均由8个通道接收机组成。其中天线为微带相控阵天线，可以满足体积小、方向性好、调试方便的要求，采用数字波束形成技术大大改善SDR（散直比Scatter-Direct-Ratio），为后续处理提供更好的基础信号。接收机主要有LNA低噪声放大器对信号进行放大，BPF带通滤波器对信号进行滤波，其工作频率为GSM 900 MHz和DCS 1 800 MHz。LO为本地振荡器，为变频产生30 MHz中频产生需要的高频信号。ADC完成中频信号数字化，采样频率为100 MHz，主要有ICS554采集卡完成。计算机完成信号的通道均衡、直达波消除、数字波束形成、0.2 s相干积累和由神经网络组成的目标检测跟踪处理系统。

目标检测的目的就是在雷达回波信号中发现目标的有无。由于雷达杂波回波更接近于混沌非线性过程，目标和杂波都变成了一段时间序列，也称为一维距离像，为提高GSM无源雷达雷达分辨率，设计如下神经网络进行目标检测。

图1 基于神经网络的GSM无源雷达系统结构示意图Fig.1 Basic structure of GSM passive radar based on neural network

2 基于感知器的最佳后验检测器

在提高分辨率的前提下，把目标或杂波看作若干相互独立的分辨（散射）单元，由此使得这些分辨单元的回波信号也是相互独立的。因此，如果通过数字波束形成技术DBF（Digital Beam Forming）获得了目标的位置和方向信息，就可以基于目标和杂波（或噪声）每个独立散射单元来的回波序列，进行目标信号的后验检测。由于这种检测器是基于目标或杂波的后验概率来实现的，因此它常被称为最佳后验检测器[7-10]。这种后验检测器完全可以通过一个感知器来实现。其检测原理如下。

假设xi代表第代表超过第i个分辨单元的采样回波信号与门限比较后的输出，并且xi=1代表超过门限，xi=0代表回波采样值低于给定的门限，那么在仅有噪声存在的情况下，这一检测系统xi的概率可以表示为：

即超过门限的信号概率为αi（这里假设高分辨雷达下的目标或杂波回波是不均匀的，也即其对应每个距离单元采样回波的统计特性是不同的），而低于门限的信号概率为1-αi。实际上，上式还可以表示成：

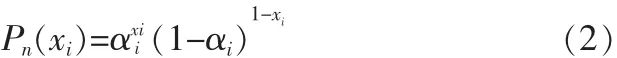
则对于N个独立分辨单元的联合检测概率可以表示为：

在目标存在的情况下，假设第i个分辨单元的发现目标的概率为βi，那么第i个分辨单元对应的判决概率为：

如果某一目标在某个距离上生成的航迹为Tr={i|i∈Fr}代表一个目标航迹 ，那么，对该目标的判决概率可以表示为：

假设目标航迹中对应的分辨单元数为M（M＜N），考虑N个分辨单元情况，则N个分辨单元中存在M个目标强散射点航迹的总条件概率为：

将式（3）与式（6）比较后，可得对数最大似然函数：

可见式（7）中只有第1项与回波信号相关，因此该式可以进一步写成：

基于式（8），我们可以重新设置一检测门限，当 LL（x1，x2，…，xN|Tr）大于该门限时

判决为H1，否则判为H0。

3 算法性能分析及评估

在目标和杂波分别存在的情况下，对充分统计量R（x）进行时间平均：

在没有目标信号存在的情况下，对应的平均值为：

同时，没有目标信号时对应的二阶矩为：

则噪声的协方差为：

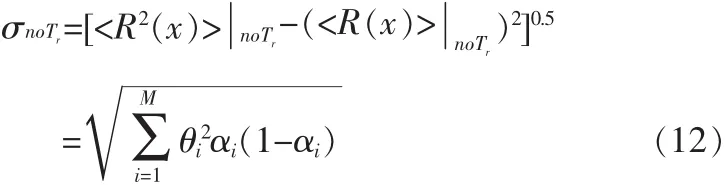
从式（9）式（12），可得对应的信噪比：

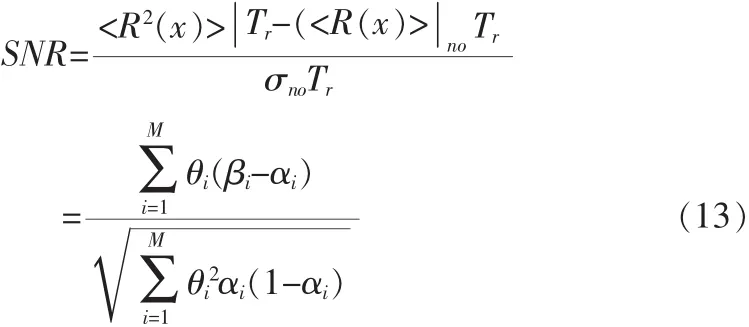
实际上，式（9）中的R（x）可以看作二项式分布。因此，其对应的发现概率和虚警概率可以分别表示为：

式中，r0为与门限紧密有关的整数。

值得注意的是，若目标回波或杂波噪声是均匀的，或者是在系统分辨率要求不高的情况下，则可以将其每个距离单元回波采样的统计特性看作是相同的。神经网络算法的航迹预测效果和卡尔曼算法处理对比如图2所示。

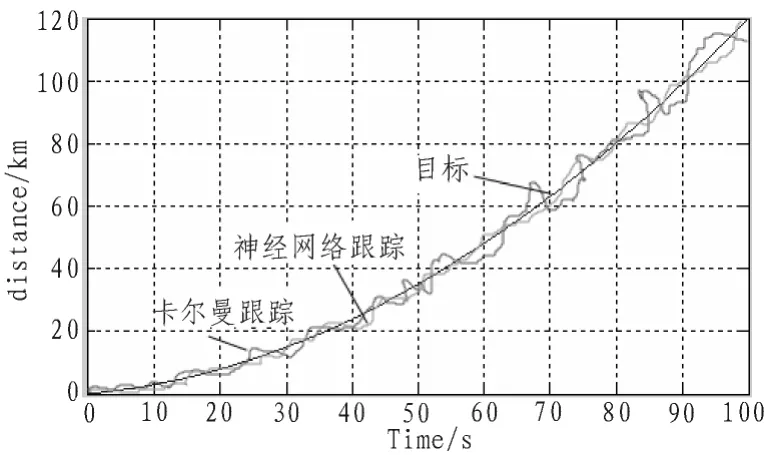
图2 为卡尔曼滤波和神经网络算法效果对比Fig.2 Result comparision of Kalman filter with Neural netwaork

图中，绿线为民航飞机的实际航迹，红线为卡尔曼滤波得到的航迹，蓝色线为感知器神经网络算法得到的航迹。从图中可以看出，神经网络感知器[11]的检测效果优于常用的卡尔曼滤波算法。

4 结束语

采用基于优化后的感知器的神经网络算法对GSM无源雷达数据进行处理，通过建立目标和杂波（或噪声）每个独立散射单元来的回波序列，可以在复杂杂波及噪声背景下获取目标数据。将神经网络应用到了GSM无源阵列雷达的数据处理，实验验证了对提高GSM无源雷达的探测能力具有重要作用。

[1]HOWLAND，PE.Passive tracking of airborne targets using only Doppler and DOA information[C]//IEE Colloquium on Algorithms for Target Tracking （1995/104），Savoy Place，London， UK，1995：7/1-7/3.

[2]ZHANG Ping-chuan，LI Bu-yin，SHEN Mao-sheen.GSM Passive Radar Target Track Prediction Based on Gray Theory[C]//Proceedings of the 2010 International Conference on AMP，2010：294-298.

[3]ZHANG Ping-chuan，CHEN Ying-song，LIBu-yin，etal.Research of Biostatic GSM Passive Radar and Positioning Algorithm [C]//Proceedingsofthe 2010 International Conference on AMP，2010：278-282.

[4]ZHANG Ping-Chuan，LI bu-yin.Probe into the cell-phone radar based on the opportunity illuminators and its key techniques[J].Information and Electronics Engineering，2008（6）：59-63.

[5] HU Yi-chung.Fuzzy integral-based perceptron for two-class pattern classification problems[J].Inform.Sci，2007，177（7）：1673-1686.

[6] Gelenbe E，Mao Z H，Li Y D.Function approximation with spiked random networks[J].IEEE Transactions on Neural Networks，1999，10（1） ：3-9.

[7]Tsoi AC，Tan S.Recurrent neural networks：a constructive algorithm and its properties[J].Neurocomputing，1997（15）：309-326.

[8]Abbasbandy S.Extended Newton’s method for a system of nonlinear equations by modified Adomian decomposition method[J].Computer， 2005（170）：648-656.

[9]Abu-Alshaikh I，Sahin A.Two-point iterative methods for solving nonlinear equations[J].Appl.Math.Comput，2006（182）：871-878.

[10]Jesús O D，Hagan M T.Backpropagation algorithms for a broadclass of dynamic networks[J].IEEE Trans.on Neural Net-works，2007，18（1）：14-27.

[11]胡艳玲，黄兴格，朱春颖，等.神经网络模型参考自适应控制在污水处理中的仿真研究[J].工业仪表与自动化装置，2011（1）：3-5，18.

HU Yan-ling，HUANG Xing-ge，ZHU Chun-ying，et al.Simulating research on neural network model reference adaptive control strategy in sewage treatment control[J].Industrial Instrumentation&Automation，2011(1)：3-5，18.