模糊控制在非线性系统中的应用研究

王丽娟

（西安工业大学 陕西 西安 710032）

模糊控制作为一种人工智能技术被广泛应用于非线性系统的控制中，解决了许多工业生产过程中的非线性、大滞后的问题[1-2]。实际在工业生产领域中除了存在的非线性及大滞后等不利于控制的现象外，还存在一个对控制非常不利的现象，即干扰。文中以某一非线性系统为例，研究了模糊控制对非线性系统的作用，及模糊控制对非线性系统中的存在的干扰是否有作用，应该如何降低干扰的影响。

1 非线性系统的数学模型

污水处理过程是一个典型的非线性系统，包含了生物反应及化学反应子过程，呈现出明显的非线性及迟滞性的特点，此外，在污水处理过程中还存在大量的干扰量，比如进水流量和底物浓度等。

文中以某一小型污水厂为例，根据物料平衡定律并对活性污泥法污水处理系统作出如下假设：

1）出水中没有微生物；

2）沉淀池为理想沉淀池；

3）出水、剩余污泥和回流污泥中的底物相同；

4）剩余污泥和回流污泥中没有溶解氧；

5）空气流量和氧总转移系数之间为指数关系。

根据质量守恒定律，底物浓度、溶解氧浓度及微生物浓度满足如下关系[3]：

已知某污水厂的运行参数，选择进水COD及溶解氧浓度为状态变量x1和x2，曝气量为操作变量u，可以得到如下系统状态方程。

因为考虑到系统的时延性，在输出y时再添加一个延时环节。

2 模糊控制系统设计

我们设计的模糊控制器以溶氧浓度do的设定值和实际测量值的误差及误差变化率e，ec作为模糊控制器的输入量，将打氧量经模糊化后转化为用模糊控制语言描述的模糊集合，建立输入和输出之间的模糊控制规则。

2.1 模糊控制器

首先，对误差e，误差变化率ec及控制量的论域做出规定，均为[-6，+6]，语言值取 5 个，分别为“负大 NB”，“负小NS”，“零 ZR”，“正小 PS”，“正大 PB”。 NB，NS，PB，PS 取梯形隶属度函数，ZR取三角形隶属度函数，如图1所示。其次，根据经验，确定if….then….形式的模糊规则，如表1所示。

表1 模糊控制规则Tab.1 Rules of fuzzy control

2.2 前馈控制器设计

根据该污水厂的进水流量数据，该污水处理厂污水流量的范围 2×106～16×106L/d 为，如图 1 所示。

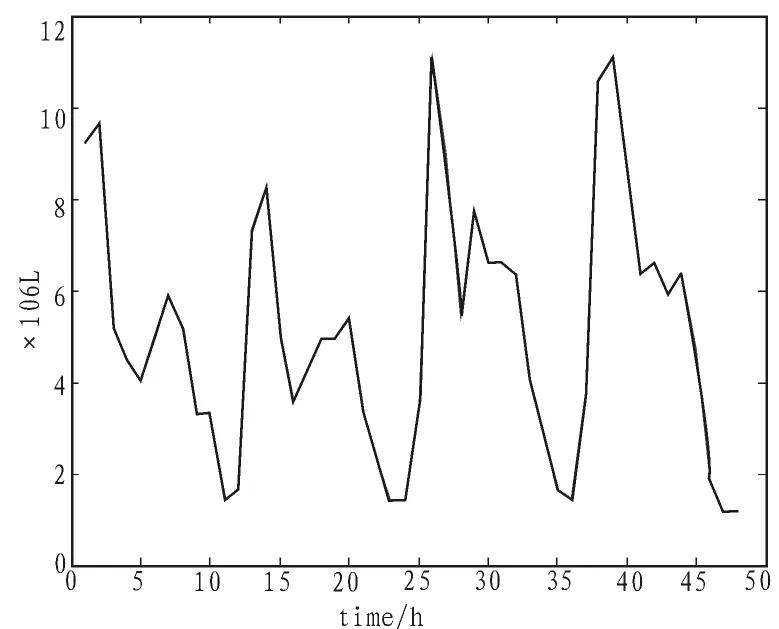
图1 进水流量数据Fig.1 Inflow datum

对其进行频谱分析出频率ω=0.26 rad/h及ω=0.52 rad/h时，进水流量数据有明显的峰值。 T1=2π/ω=2π/0.26≈24 h，T2=2π/0.52≈12 h，可以对其建立如式（5）所示的一般意义上的干扰模型。

利用最小残差法对其进行拟合，得到进水流量数学模型，如式（6）所示。

根据常规前馈控制器Gff设计方法[4]，设计结果如式（9）所示。

3 系统仿真模型

在MATLAB软件的Simulink环境下建立系统的仿真模型，其中重点是系统状态方程模型的建模。S-function模块库中的状态方程模块只适用于线性定常系统。文中的系统为非线性系统，采用编写S-function函数的途径来为其建模。

S-function是System function的简称，其功能是通过MATLAB或C语言程序，建立一个能和Simulink模块库中模块一起使用的新模块，从而实现所需功能。利用S-function可以定义自己的差分方程，离散系统方程，或者是将要在Simulink图块中用到的任意一种算法。编写S-function需要完成以下6个子程序：

1）mdlInitializeSizes初始化（设置各种参数值）；

2）mdlDerivatives（t，x，u）输出值 sys为状态值的微分；

3）mdlUpdate（t，x，u）输出值 sys 为状态值在下一时刻的更新值；

4）mdlOutputs（t，x，u）输出值 sys 为输入值与状态值的函数；

5）mdlGetTimeOfNextVarHit（t，x，u）输出值 sys 为下一次被触发的时间；

6）mdlTerminate（t，x，u）模拟结束。

Simulink模型示意图如图2所示。

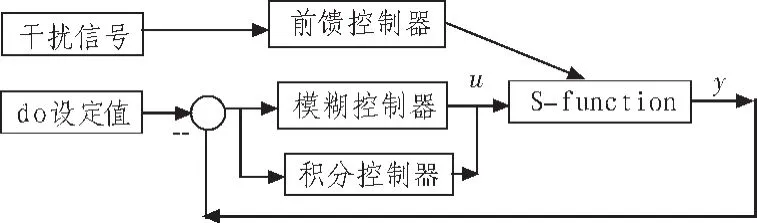
图2 控制系统结构示意图Fig.2 Structure of control system

图2中的S-function用来实现污水处理系统的状态空间模 型， 主 要 包括了 mdlInitializeSizes，mdlUpdate （t，x，u）和mdlOutputs（t，x，u）3 个最基本子程序[5-6]。3 个函数具体内容如下所示。

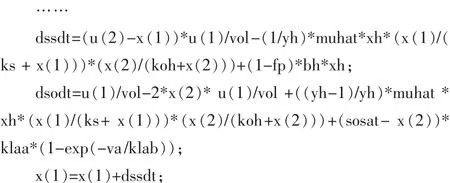
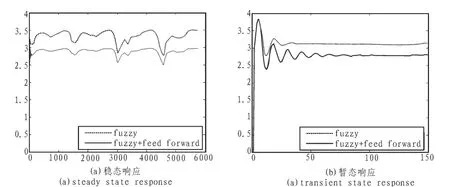
图3 仿真结果Fig.3 Simulation result

从图3中可以看出，对污水处理厂的进水流量进行前馈补偿后，系统暂态响应和稳态响应都发生了变化。从图3（a）可以看出，单独使用模糊控制系统最终稳态误差较大，达到16.7%，而加入前馈补偿后，系统稳态误差大大减小，趋近于0。从图3（b）可以看出，单独使用模糊控制时，系统暂态响应速度较快。综合来看，将模糊控制[7]和前馈补偿结合才可以取得良好的控制效果。

4 结 论

本文通过为污水处理这样一个典型非线性系统[8]设计控制系统，研究了模糊控制对非线性系统的控制效果。仿真结果表明，模糊控制可以解决非线性系统呈现的非线性、滞后性问题，但是对于非线性系统中存在的干扰问题作用有限，而前馈补偿仍是解决干扰问题的主要手段。

[1]Yin M T，Stenstrom M K.Fuzzy logic process control of HPO-AS process[J].Journal of Environmental Engineering，1996，122（6）：484-492.

[2]HU Yu-ling，CAO Jian-guo，QIAO Jun-fei.Fuzzy neural network control of activated sludge system [J].Journal of System Simulation，2005，10（17）：2541-2544.

[3]Olsson G.污水处理系统的建模、诊断和控制[M].高景峰，彭永臻，译.北京：工业出版社，2005.

[4]朱学峰，刘桂香，陈菊，等.自来水厂出水浊度的前馈反馈智能控制[J].控制工程，2010，3（17）：290-296.

ZHU Xue-feng，LIU Gui-xing，CHEN ju，et al.Forward and feedback intelligent control of outwater coming from water Factory[J].Control Engineering of China，2010，3（17）：290-296.

[5]王洪斌，吴健珍，杨香兰，等.Simulink（S-function）在复杂控制系统仿真中的应用 [J].系统仿真学报，2001，8（13）：131-133.

WONG Hong-Bin，WU Jian-Zhen，YANG Xiang-Lan，et al.Implications of simulink to Simulation for complex control systems[J].Journal of System Simulation，2001，8（13）：131-133.

[6]郭红梅，于佐军.Simulink（S-function）在非线性系统控制仿真中的应用 [C]//2007年中国控制与决策学术年会论文集，2007：69-74.

[7]向平，梁筱.基于模糊控制的无刷直流电机的建模及仿真[J].工业仪表与自动化装置，2011（1）：39-42.

XIANG Ping，LIANG Xiao.Model and system simulation of the BLDCM based on fuzzy controler[J].Industrial Instrumentation&Automation，2011（1）：39-42.

[8]刘上，刘红军，徐浩海，等.单向阀流路系统自激振荡特性研究[J].火箭推进，2011（3）：1-5,17.

LIU Shang，LIU Hong-jun，XU Hao-hai，et al.CResearch of self-oscillation characteristics of check valve flow-path system[J].Journal of Rocket Propulsion，2011（3）：1-5，17.