基于Bayes BootStrap的特种设备可靠性模型参数确定方法

江赛

（海军工程大学 科研部，湖北 武汉 430033）

航海特种设备直接影响到航行安全，确保其可靠性十分重要。预先维修一般是指在设备发生故障之前提前采取适当的处理措施，达到增强设备技术完好性，提高设备可靠性的目的。将预先维修理论在航海特种设备的维修保障十分必要。然而，运用预先维修理论进行推断时需要利用验前信息，获取的验前信息是否准确将对最终得到的预测结果产生极大的影响。一般地，获取先验分布函数一般可以采用3种方法[1]：1）利用历史资料，特别是以前做过的试验数据资料，获取分布函数；2）通过理论分析或者仿真获取分布函数；3）凭藉经验的“主观概率”法，例如“专家打分法”获取分布函数。对此 Jeffreys[2]，Jaynes[3]，Stein，Villegas[4]等人作了专门研究，得出“同等无知原则”、“位置参数（Location Parameter）的验前分布”、“尺度参数 （Scale Parameter） 的验前分布”、“Jeffreys 规则”[5]等方法和结论。Bayes Bootstrap方法（也称随机加权法[6]）也是一种关于估计误差的统计处理方法，它的基本思想是用估计误差的随机加权统计量去逼近估计误差的分布。Bayes Bootstrap方法没有用到大样本，因此在小子样情况下，随机加权法具有较好的应用效果。考虑到航海特种设备小子样特点，文中将Bayes Bootstrap方法应用于航海特种设备维修时间模型参数的确定。

1 Bayes BootStrap方法的基本原理

设随机子样 X=（x1，x2，…，xn）来自未知的总体分布 F，θ=θ（F）是总体分布F的某个参数（如均值、方差等），Fn是由子样X=（x1，x2，…，xn）得到的抽样分布函数（通常取 X 的经验分布），ˆ（Fn）为 θ的估计。 记

式中：Tn——表示估计误差。

记

式中：Vi——表示具有Dirichlet分布的随机变量，i=1，2，…，n；

Dn——表示Tn的随机加权统计量。

随机加权法就是以Dn的分布去模拟估计误差Tn的分布。

考虑到海航特种设备维修性数据少的现状，文中采用Bayes BootStrap方法确定其维修时间分布模型参数，采用Monte-Carlo方法进行模拟计算，计算步骤[7]如下：

1）在区间[0，1]上产生n-1 个随机数vi，i=1，2，…，n-1，并且使vi在区间[0，1]上具有独立性和均匀性。

2）对生成的vi按从小到大的次序进行排序，得vi，…，vn-1的次序统计量为v（1），…，v（n-1），并令v（0）=1，v（n）=1。

则Vi=v（i）-v（i-1），（i=1，…，n）的联合分布为 Dn（1，1，…，1），（V1，…，Vn）就是我们需要的随机向量。

3）重复抽样N次，由公式（4.2.17）计算相应的Dn（i），i=1，2，…，N。

4）用Dn（i），i=1，2，…N作为Tn的估计，由公式（4.2.16）得

由此得到θ的值。

2 利用Bayes Bootstrap方法确定可靠性分布模型的参数

一般地，航海特种设备维修时间服从对数正态分布，记维修时间的概率密度函数[8]为：

修复率函数为：

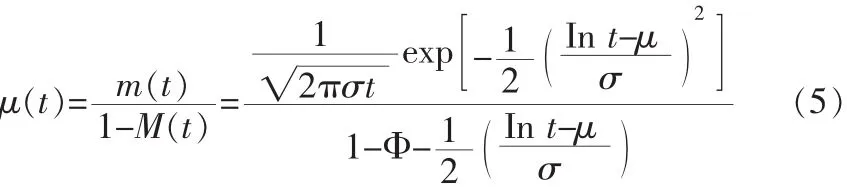
平均修复时间为：

最大修复时间为：

式中，ZP是给定概率为P的分位数，文中取0.95，Z0.95≈1.65。

下面用Bayes BootStrap方法对某型航海特种设备估计误差进行推断，从而得到准确的参数值。计算步骤如下：

1）在区间[0，1]上产生 19 个随机数vi，i=1，2，…，19 并且vi在区间[0，1]上具有独立性和均匀性。

2）对生成的vi按从小到大的次序进行排序，得vi，…，v19的次序统计量为v（1），…，v（19），并令v（0）=0，v（20）=1。

则Vi=v（i）-v（i=1），（i=1，…，20）的联合分布为D20（1，1，…，1），（V1，…，V20）就是我们需要的随机向量。

由式

计算相应的 Dμ、D2。 并重复抽样N次， 得到Dμ（i），D2（i），（i=1，…，N）。

4）用Dμ（i）、Dσ2（i），i=1，…，N作为估计误差的Tn逼近，由公式（3）有

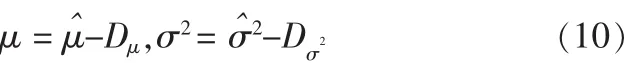
根据实测试验数据得到μ和σ2的一组估计，再对所得的估计值做点估计得μ=3.470 5，σ2=0.405 3。

由此得这种某航海特种设备的维修时间服从参数为（3.470 5，0.405 3）的对数正态分布，即 lnt～N（3.470 5，0.405 3）。

3 可靠性指标的计算

由上节的计算结果得给定小样本数据的维修时间概率密度函数为：

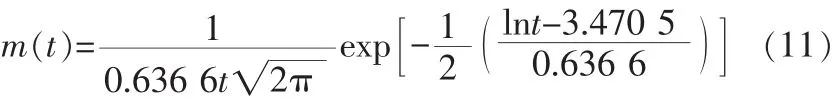
修复率函数为：

维修时间分布的概率密度函数和修复率函数分别如图1、2 所示。

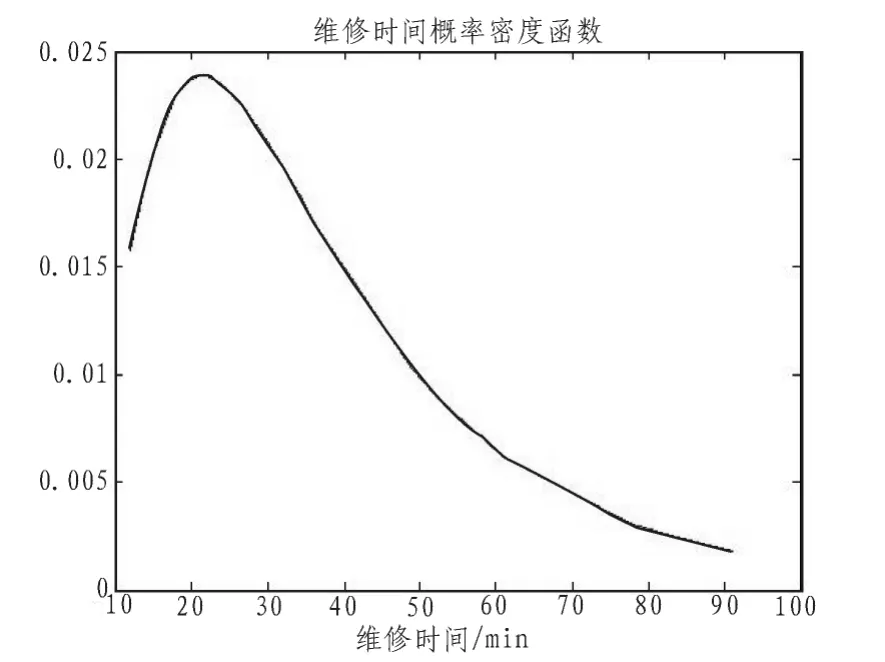
图1 维修时间分布概率密度函数Fig.1 Probability density function

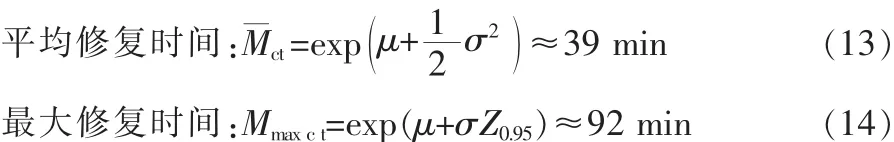
4 结 论

运用预先维修理论进行推断时需要利用验前信息，即确定预先维修的数学模型。本文将Bayes BootStrap方法应用于航海特种设备维修模型参数的确定，结合实际小字样试验数据，计算结果表明，修复时间的平均值为39 min；所有维修措施的50%在32 min内将能完成；所有维修措施的95%在92 min内都能完成。针对某型航海特种设备的技术指标都规定基层级的平均修复时间Mct≤30 min，而文中计算得出的分钟，可知该型航海特种设备使用中的维修性有所下降，需查找具体原因减少维修时间。

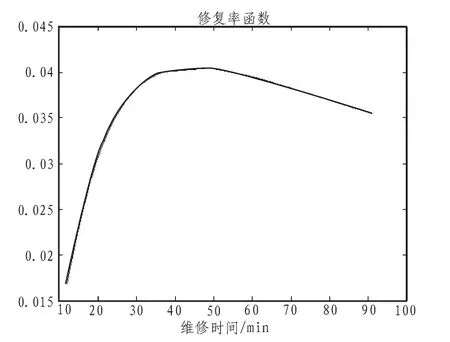
图2 修复率函数Fig.2 Repair rate function

[1]唐雪梅，张金槐，邵凤昌，等.武器装备小子样试验分析与评估[M].北京：国防工业出版社，2001.

[2]Jeffreys H.Theory of Reliability[M].London：Clarendon Press，1961.

[3]Jaynes E T.Prior probability[J].IEEE Trans.on Systems Science and Cybernetics，1968（4）：227-241.

[4]Villegas C.On the representation of ignorance[J].Jour.Amer.Statist.Assoc，1977（72）：651-654.

[5]张金槐.Bayes试验分析中验前分布的表示[J].国防科技大学学报，1999，21（6）：109-113，118.

ZHANG Jin-huai.Bayes test analysis for the prior distribution of representation[J].Journal of National University of Defense Technology，1999，21（6）：109-113，118.

[6]Walter G G ，Hamedani G G.Bayes empirical bayes estimaion for discrete exponential families[J].The Annals of Statistics，1989（41）：101-119.

[7]段晓君，王正明.小子样下的Bootstrap方法[J].弹道学报，2003，15（3）：1-5.

DUAN Xiao-jun，Wang Zheng-ming.Under small sample Bootstrap method[J].Journal of Ballistics，2003，15（3）：1-5.

[8]金星，洪延姬，沈怀荣，等.工程系统可靠性数值分析方法[M].北京：国防工业出版社，2002：216-227.