基于自适应遗传算法的关联运输调度问题

广东工业大学自动化学院 肖 丹 蔡延光 汤雅连 胡夏云 徐山峰

基于自适应遗传算法的关联运输调度问题

广东工业大学自动化学院 肖 丹 蔡延光 汤雅连 胡夏云 徐山峰

利用引入了混沌扰动的一种改进的自适应遗传算法来解决一类关联运输调度问题IVRP（Incident Vehicle Routing Problem）模型。虽然M.Srinivas提出的自适应遗传算法既保护了最优个体又加快了较差个体的淘汰程度，但不容易跳出局部最优解，相邻进化代数间的参数缺乏连续性，所以，提出了一种新的自适应遗传算法，为避免近亲繁殖提出了改进策略，同时考虑到变异概率的大小可能导致破坏种群模式或减弱抑制早熟的能力，设计了相关的自适应变异概率。研究表明，该改进的算法在解决关联物流运输调度问题具有有效性和适用性。

关联物流运输调度；自适应；遗传算法

1.引言

物流配送车辆调度问题[1]包括运输路线安排问题（VRP）和车辆调度问题（VSP），被认为是NP-hard问题。运输调度问题[2]的目的是在满足一定的约束条件（如车辆限制、时间限制、载重限制、运输能力限制等）下，组织适当的行车路线和任务分配，达到一定的目标（如成本极少、路程最短、时间最少、使用车辆数尽量少等）。

客户通常将所有零件商品供货交给一个物流运输公司来为其配货，而每个客户所需货物有一定的关联性，物流公司须考虑怎样进行车辆分配和寻求最优配送路线以达到最低的物流成本来为多个这种性质的客户配送货物，这样的调度问题称之为关联物流运输调度问题（Incident Vehicle Routing Problem）。国内外学者还没有人对此问题进行研究，该问题是由蔡延光教授首次提出，因而具有理论研究意义和实际应用价值。研究学者们对VRP[3～8]、MVRP[9]（Multi-Depot Vehicle Routing）、AVRP[10，11]（Allied Vehicle Routing Problem）、DVRP[11，12]（Deterministic Vehicle Routing Problem）等问题的研究方法和已取得的成果对研究该问题都具有很大的借鉴意义。

由于车辆在配送过程中，会受到道路路况的影响，而单车场单车型是多车场多车型的基本模型，所以本章研究较简单的模型——单车场单车型单配送中心带软时间窗和道路容量约束的RVRP，并提出了一种自适应遗传算法来对所建立的模型求解。

2.单车场RVRP模型建立

2.1 问题描述及假设

本章研究的问题基于以下假设：

（1）1个车场，l个客户（1，2，…，l），客户需求已知，1个配送中心；

（2）每辆车有里程约束和载重约束，同种车型；

（3）非满载，软时间窗约束；

（4）道路容量动态约束，不考虑交叉口冲突模型等，车辆均在主干道上行驶，道路宽度恒定。

2.2 模型的建立

有l个客户（1，2，…，l），第i个客户的货运量为 gi（ i ＝1,2,...l ），需要从车场0将货物运到客户位置，车场可派出载重为q的货车，已知 gi＜ q ，客户要求送货的时间窗为[ ， ]，每小时等待费用和延迟费用分别为 c1和 c2，车辆早到或者晚到，都会受到惩罚。 t0i表示车辆从配送中心到i的时间。

预先估计车辆数[13]。可以按照式(1)估算车辆数。式中，[ ]表示不大于括号内数字的最大整数； 0 ＜α＜1，是对装车（或卸车）的复杂程度及约束多少的估计。

以 cij表示为从点i到点j的运输成本(距离、费用、时间等)， cij＝ cji。假设客户i，j之间的距离为 dij。关联系数为r， rij表示点i处的货物与点j处货物的关联系数。为简化问题，用 wij表示路况系数， wij越大，说明路况越差，交通越堵塞，车辆通过此段路的时间越长，成本越高；反之，成本越低。目标是使运输成本最低。定义变量如下：

建立数学模型

目标函数式(4)表示总运输成本最低， Ti表示到达客户i的时间。(5)为车辆行驶里程约束，其中dijk表示车辆k从i行驶到j的路程，n是车辆k服务的客户数目，最大为N。(6)和(7)表示两个变量之间的关系。(8)表示车辆服务i后直接行驶到j为其服务。(9)表示每个客户只由1辆车来服务且每个客户都能得到服务。(10)表示每辆车所运送的货物重量不能超过车辆载重限制。(11)表示每辆车的客户总数小于等于总客户数目。(12)为关联系数 ijr的取值约束。(13)ijt表示从i到j的行驶时间，ijw为路况系数， ijw越大，表示路况越差；反之，越好。(14)表示行驶总时间，mt为卸货时间。

3.自适应遗传算法设计

本节设计的自适应遗传算法[14]包括避免近亲繁殖的杂交策略与改进的交叉概率。文献[15]中提出到了M.Srinivas提出的自适应遗传算法，该算法是根据每代个体适应度的改变来自适应地改变pc和 pm，既保护了最优个体又加快了较差个体的淘汰程度，但以个体单位改变它们缺乏整体协作精神，在某些情况下（如整体进化的停滞期），将不容易跳出局部最优解，相邻进化代数间的参数缺乏连续性，所以，本节提出了一种新的自适应遗传算法，采取在交叉操作后保留适应度值最大个体的策略，设计与进化代数相关的交叉概率和自适应变异概率。

3.1 交叉算子

交叉算子主要用于产生新个体，实现算法的全局搜索能力。考虑到整个种群的变化趋势及每个个体的变异机会，本节设计了与进化代数相关而与个体适应度无关的交叉概率计算公式，如式(16)。t为当前进化代数， Tg en为预设的最大进化代数， pcmax为预设最大概率，pcmin为预设最小概率， pc( t)为当前种群的交叉概率。

3.2 变异算子

交叉算子起着全局搜索的作用，变异算子主要是产生新个体和抑制早熟。设计变异概率的总趋势是逐渐减小而使群体迅速集中。下面是本节设计的自适应变异概率。maxmp 是预设的最大变异概率，minmp是预设的最小变异概率，）（tpm是第t代个体进行变异的概率。

3.3 随机扰动[14]

Step1：对适应度较小的90%对应的优化变量按式（20）加一混沌扰动，按式（19）映射为优化变量，进行迭代计算。式（21）中的θ随迭代次数增加为不断变化，迭代向较优解逼近，直到满足式（22）。k为迭代次数。

Step2：φ*为当前最优解[10](，…，)映射到[0，1]的向量，φk为迭代k次后的混沌向量，为随机扰动后的混沌向量，θ取值为(0，1)，可由式（21）来计

表1 客户信息一览表

表2 货物间的关联系数

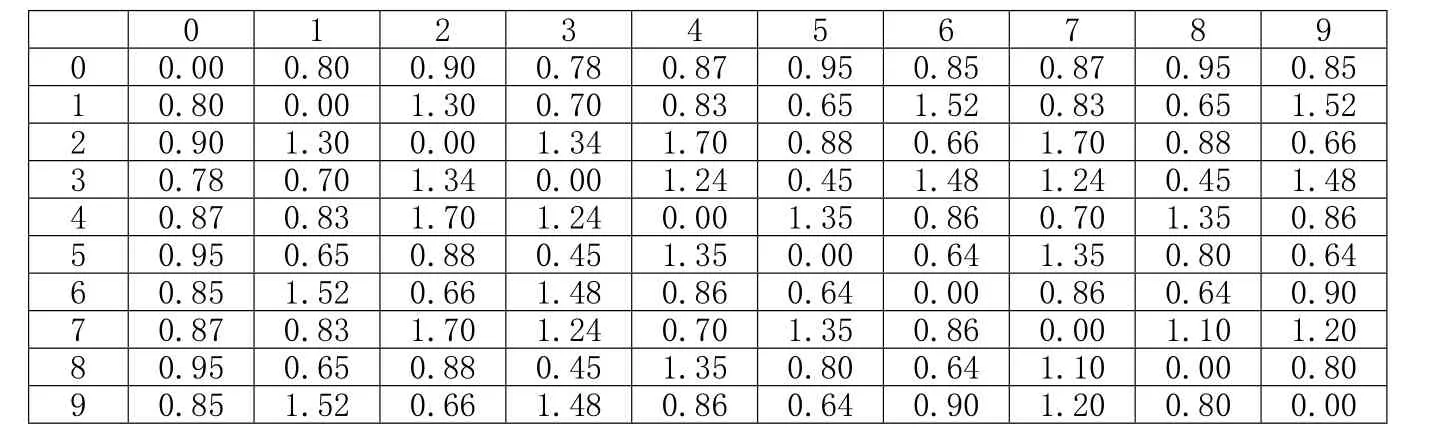
表3 客户之间的道路路况系数

表4 本算法最优配送路径

表5 两种算法对比结果

算，m依目标函数而定，这里取5＝m。

Step3：对新产生的种群进行适应度值计算，若满足终止条件，输出最优值；否则，返回Step1。

3.4 自适应遗传算法

自适应遗传算法流程图如图1所示，具体步骤如下：

Step1：初始化。通过随机发生器产生l个客户的全排列，并将首末位置0，表示从车场出发最终回到车场。确定种群规模、交叉概率、变异概率、进化代数等参数，并均匀地随机产生初始种群，其中包含m个染色体。

Step2：适应度值计算。计算相应的目标函数值以及适应度函数值jf，j=1，2，…，m。对于极大值问题，适应值就等于目标函数值。用当前群体中最佳染色体的目标函数值Z与当前染色体的目标函数值iZ的比值作为适应度值。

Step4：对选择后的种群以改进的交叉概率和变异概率进行操作，生成新种群。

Step5：计算新种群中染色体对应的目标函数值及适应值，并对适应度较小的个体进行混沌扰动，若该新个体的适应度值大于原个体，则替换原个体，否则不变。迭代多次。

Step6：满足条件，输出最优解，算法终止；否则，转步骤Step2。

4.仿真分析

某物流中心为9个客户配送货物，如表1所示。有载重为8吨的大型车辆，每辆车的最大里程为200km，车速为60km/h。货物关联系数如表2所示，路况系数如表3所示。等待费用和延迟费用分别为10元/h和100元/h，不考虑吃饭时间。车场为（0，0）。单位配送费用为1元/t*km。最早发车时间7:00。

5.结束语

本章研究了带道路容量动态约束的关联物流运输调度问题。研究成果如下：

(1)为了整体把握算法，克服参数计算仅与每一代个体的情况有关，而相邻代数之间的参数计算缺乏连续性的局限性，设计了一种改进的自适应遗传算法，既避免了近亲繁殖，又考虑了进化代数之间的关系，设计的相应的交叉概率和自适应变异概率；

(2)考虑了道路路况对配送时间的影响，最终体现在是否符合时间窗要求；

(3)考虑了货物性质关联对不同性质的货物是否能同载的约束。用此算法对所建立的模型求解。实例证明，本章提出的自适应遗传算法能有效求解此类问题，在下一步研究中，可以延伸至求解多个扩展特征(需求关联、时间关联等)的关联运输调度问题。

[1]张潜,高立群,胡祥培,等.物流配送路径多目标优化的聚类-改进遗传算法[J].控制与决策,2003,18(4):418-422.

[2]任中明.运输调度问题的智能求解机制研究[D].广州:广东工业大学,2011.

[3]屈援,汪波,钟石泉.单车场多送货点车辆路径问题的改进遗传算法[J].计算机工程与应用,2007,43(25):237-239.

[4]G.B.Alvarenga,G.R.Mateus,G.de Tomi.A genetic and set partitioning two-phase approach for the vehicle routing problem with time windows[J].Computers&Operations Research,34(2007)1561-1584.

[5]Hong Ma,Brenda Cheang,Andrew Lim,et al.An investigation into the vehicle routing problem with time windows and link capacity constraints[J].Omega,2012,40:336-347.

[6]Christian Prins.A simple and effective evolutionary algorithm for the vehicle routing problem[J].Computer&Operations Research 31(2004):1985-2002.

[7]Yanis Marinakis,Magdalene Marinaki,Georgios Dounias.A hybrid particle swarm optimization algorithm for the vehicle routing problem[J].Engineering Applications of Artif i cial Intelligence 23(2010):463-472.

[8]G.Nilay Yucenur,Nihan Cetin Demirel.A new geometric shape-based genetic clustering algorithm for the multi-depot vehicle routing problem[J].Expert Systems with Appications 38(2011):11859-11865.

[9]李敏,郭强,刘红丽.多车场多配送中心的物流配送问题研究[J].计算机工程与应用,2007,43(8):202-204.

[10]蔡延光,李永生,林灼强,丁志勇.带中转点的联盟运输调度的遗传算法研究[J].计算机应用研究,2007,24(11):82-84.

[11]陈金,蔡延光.带时间窗的中转联盟运输调度问题的混合算法研究[J].工业控制计算机,2010,23(1):70-72.

[12]Rita Macedo,Claudio Alves,J.M.Valerio de Carvaiho,Francois Clautiaux,Said Hanafi.Solving the vehicle routing problem with time windows and multiple routes exactly using a pseudopolynomial model[J].European Journal of Operational Research,214(2011):536-545.

[13]王占锋,张翠军,许冀伟等.求解非满载车辆调度问题的改进遗传算法[J].计算机工程与设计,2008,29(15):3991-3994.

[14]魏明,蔡延光.一种基于混沌领域搜索的自适应遗传算法[J].计算机应用研究,2009,26(2):465-467.

[15]李青欣.自动导引车路径规划遗传算法研究[D].广州:广东工业大学,2011.

国家自然科学基金项目(61074147，60374062)；广东省自然科学基金项目(S2011010005059)；广东省教育部产学研结合项目(2011B090400460)；广东省自然科学基金团队项目(8351009001000002)。

肖丹（1987—），男，湖南永州人，硕士研究生，研究方向：物流信息技术与应用。

蔡延光（1963—），男，湖北咸宁人，广东工业大学自动化学院教授，博士生导师，主要从事组合优化、人工智能、决策支持系统等的研究。

汤雅连（1986—），女，湖南常德人，硕士研究生，研究方向：物流信息技术与应用。

胡夏云（1987—），女，江西宜春人，硕士研究生，研究方向：物流信息技术与应用。

徐山峰（1987—），男，福建莆田人，硕士研究生，主要研究方向：物流信息技术 与应用。