测量不确定度评定方法在电学计量中的应用研究

江苏省计量科学研究院 马建龙

测量不确定度评定方法在电学计量中的应用研究

江苏省计量科学研究院 马建龙

介绍了测量不确定度评定理论，论述了在对电学仪器进行计量校正所采用的理论，并分析了各种不确定度的特点和适用性，为电学仪器的计量提供参考并指出发展方向。

测量；不确定度评定；静态不确定度评定；动态不确定度评定

1.引言

测量的目的是根据测量到的数据，对被测事物的优劣进行评定，测量的精度直接影响到一个产品的质量和企业的经济效益，面对经济全球化的今天，测量精度甚至影响到国家的进出口经济效益。近年来，各国的计量学者在研究测量方法的科学行、准确性方面做了很多研究，随着科技的发展以及各种统计理论的成熟化，导致测量硬件和软件极大的发展的同时，对计量的准确性提出了更高的要求。

在对电学仪器计量的实验中，测量的结果并不是被测产品的真实值，最早引用“误差”的概念引起了不小的争论，直到1927年，德国物理学家海森伯基于量子力学理论提出了不确定关系，随后，不确定度评定理论被广泛的引用在对电学计量中。

2.不确定度标准

为了消除使用“误差”概念而引起的争论，随着经济一体化、贸易全球化的进程加快的同时，也间接的促使要求各国所进行的测量和所得的测量结果应具有统一的评定标准，避免同种产品在不同国家的计量中存在的标准差异而引起不必要的损失，测量不确定度在这种情况下经过一系列的发展阶段，最终形成国际标准。

图1 不确定度评定过程

表1 测量方程及数据

表2 测量结果不确定度报告

1986年，由国际标准化组织(ISO)、国际电工委员会(IEC)、国际计量委员会(CIPM)、国际法制计量组织(OIML)组成了国际不确定度工作组制定了用于计量、标准、质量、认证、科研、生产中的不确定度标准指南。国际不确定度工作组经反复修改，1993年制定了《测量不确定度表示指南(Guide to the Expression of Uncertainty in Measurement)》(简称GUM)，指南得到了BIPM、OIMI、ISO、IEC及国际理论与应用化学联合会(IUPAC)、国际理论与应用物理联合会(IUPAP)、国际临床化学联合会(IFCC)的批准，由ISO出版。国际不确定度工作组制定的GUM是国际组织的重要权威文献，自1993年出版以来，得到了广泛的应用和发行。目前GUM在全世界的执行已推动不确定度达到了最新水平，它是现代不确定度方法与应用的根据。中国计量科学研究院于1996年11月制订了《测量不确定度规范》。1999年1月我国国家质量技术监督局批准颁布了基本等同采用GUM的国家计量技术规范JJFl059—1999《测量不确定度评定与表示》。

3.评定算法

随着理论研究的不断完善和成熟，运用各类先进的算法建立测量系统模型的研究日益成为计量工作者的研究热点。在ISO国际标准文件中，并没有对这些特殊测量系统的不确定度的算法进行规定，但是研究者根据文件中的基本规定，经过数学定理推导出它们的不确定度的评定方法。

目前国内常用的不确定度评定方法主要分为两种：基于统计理论的静态不确定度评定的传统方法和基于新模型、新理论的动态测量不确定度评定方法。不确定度评定过程如图1所示。

3.1 静态不确定度评定

刘智敏等人[1]提出的采用最大方差法来对测量结果的标准不确定度进行评定；宋明顺等人[2]给出了测量值为一种最小二乘测量结果扩展的不确定度评定公式，此测量结果服从正态分布且相互独立，并依据实际应用中得以验证，弥补了GUM在该问题表述上的不足。张海滨等人[3]对测量不确定度评定模型进行了验证，用埃奇沃思级数展开形式来表示测量数据的分布函数，然后由蒙特卡罗模拟法产生大量符合此分布函数的测量数据的模拟值，把计算出的模拟值的标准差作为不确定度评定的验证值，从而能实现对各种不确定度评定模型的验证，并且用实例分析了此方法的有效性。

宋明顺提出的最小二乘测量评定理论基于“测量值mn服从正态分布，n=1，2，3，…，t。

上述假设是根据中心极限定理以及大量的统计实验做出的，具有广泛的适用性。

假设2：各个测量值mn都是相互独立分布的。

最小二乘未知量xi的线性表示为：

式中：A为测量方程系数矩阵；P为测量值mn权值矩阵；L为测量值mn矩阵；X为未知量xi的矩阵，是待求的矩阵。

经过线性变换以后得到未知量xi的线性表达式为：

基于上述分析，服从正态分布的最小二乘未知量xi的概率分布为：

基于上述理论分析，采用不同的测量仪器和方法对图2中的电阻进行测量，测量方程及数据如表1所示。测量结果不确定度报告见表2。

3.2 动态不确定度评定

朱坚民等人[4]-[5]针对测量数据少、分布难以确定等GUM无法进行评定的情况，提出将灰色系统理论、模糊集合理论、贝叶斯统计理论、神经网络理论等用于测量不确定度的评定，取得了一定的研究成果，为测量不确定度的非统计评定提供了理论基础。田口玄一[6]-[7]创立了测量质量工程学，其可分为两部分：线内测量质量工程学和线外测量质量工程学。

动态测量不确定度的理论是现代误差理论的精髓，也代表了当代误差理论的研究方向及进展。在理论上告别了以统计理论为基础的传统方法。弥补了基于统计理论的传统评定方法的不足，由于起步较晚，动态不确定度评定不能适用所有统计理论中的不确定度问题，如果可以把动态静态不确定度结合使用，会收到很好的效果。

以王中宇提出将灰色系统理论为基础，来说明动态不确定度评定方法。标准不确定度的灰色评定模型[8]。

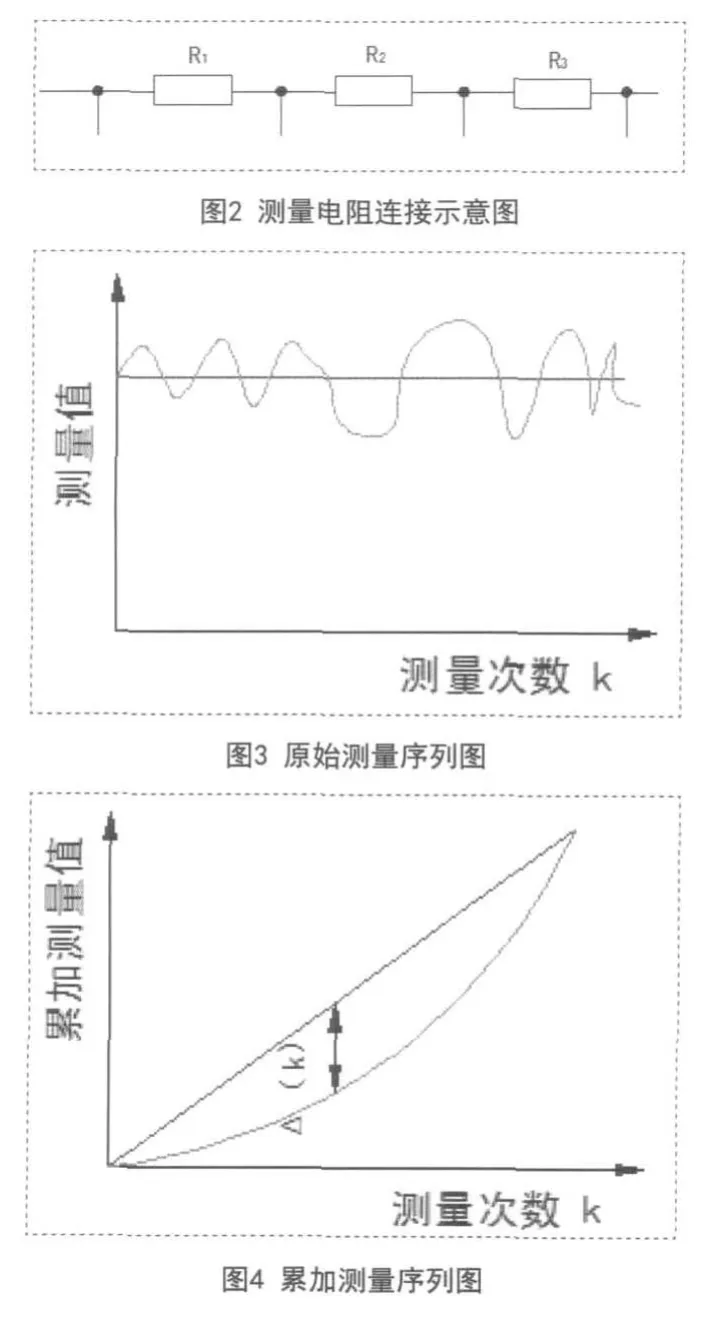
在测量过程中，由于测量误差的存在，使测量结果在一定程度上是不确定的，因此测量系统可看作为一个灰色系统[4，5]。

若有一组测量数据序列X=[(sk)|k=l，2，...，n]，以测量次数k为横坐标，以测量值为纵坐标作如图3所示的原始测量序列图。

对数据序列：

作一次累加生成，得到：

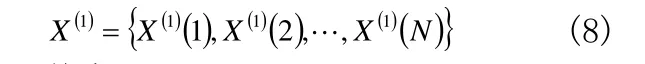
其中

构造累加矩阵B与常数项向量YN，即：

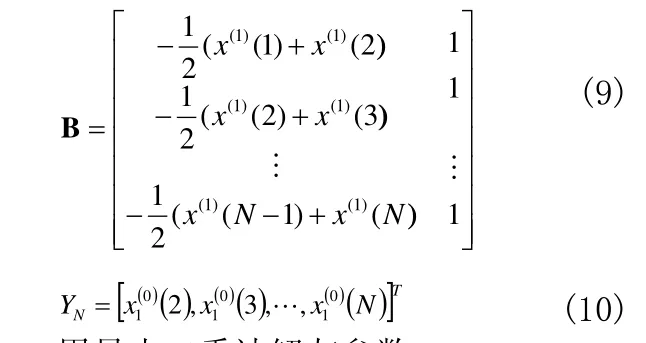
用最小二乘法解灰参数

将灰参数代入时间函数：

“今年省公司制定了按照各个分公司下属加油站同期比给予奖励的政策。例如，如果这个加油站这个月与去年同期相比有增量，就按增量的比例发放奖金。”范好光告诉记者，这些奖金直接发放到站经理手里，再由站经理按照站里员工贡献情况兑现到个人。

对求导还原得到：

计算与之差e(0)(t)及相对误差e(t)

模型精度检验及应用模型进行预报。

在图4中，红线为理想测量过程，绿线为实际测量过程，理想测量过程和实际测量过程的差异程度反映了两测量过程之间的误差，也同时反映了测量数据样本的分散程度，也就是测量结果的标准不确定度的大小。

为了分析模型的可靠性，必须对模型进行精度检验。目前较通用的诊断方法是对模型进行后验差检验。即先计算观察数据离差s1：

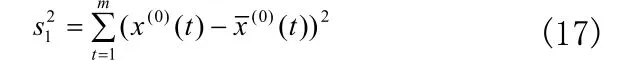
及残差的离差s2：

再计算后验比 ：

以及小误差概率：

根据后验比c和小误差概率p对模型进行诊断。当p>0.95和c<0.35时，则可认为模型是可靠的，可用于预测。这时可根据模型对系统行为进行预测。见图3、图4。

当所建立模型的残差较大、精度不够理想时，为提高精度，一般应对其残差进行残差GM(1，1)模型建模分析，以修正预报模型。通过仿真及应用示例表明[3，13]，由公式(17)-(20)表示的标准不确定度的灰色评定模型在小样本或测量数据分布不明确的条件下均可取得可靠的评定结果。

4.结论

1)通过对不确定度评定的标准研究，得到了测量不确定度评定在电学计量中的应用是非常重要的，评定算法精确性、科学性等因素直接影响电学计量的好坏；

2)通过对静态不确定度评定与动态不确定度评定的比较，得到未来测量不确定度的发展方向为动态不确定度评定与静态测量不确定度评定相结合，使得电学计量中应用测量不确定度进行评定时更加精确、科学。

[1]刘智敏.不确定度评定的一种方法-最大方差法[J].宇航计测技术,1998(1):24-35.

[2]宋明顺,顾龙芳,陈意华.最小二乘测量结果不确定度的评定及案例[J].计量技术,2000(1):43-45.

[3]张海滨,王中宇,刘智敏.测量不确定度评定的验证研究[J].计量学报,2007(3):193-198.

[4]朱坚民,王中宇,夏新涛.测量不确定度的评定与展望[J].洛阳工学院学报,2002(2):21-24.

[5]王中宇,朱坚民.几种测量不确定度的非统计评定方法[J].计量技术,2001(4):48-50.

[6]田口玄一.MTS法和诊断问题.标准化和品质管理,1999(10):63-69.

[7]田口玄一.MTS法的信噪比.标准化和品质管理,1999(9):63-70.

[8]Wang Zhongyu.Grey EvaIuation of Measurement Uncertainty,The JournaI of Grey System,1999,4,347-352.

马建龙（1966—），男，回族，江苏南京人，大学本科，工程师，从事电学仪器计量研究。