中国宏观经济周期波动的协动性与非对称性研究

唐晓彬，向蓉美

（1.成都信息工程学院统计学院，成都 610103；2.国家统计局统计信息技术与数据挖掘重点开发实验室，成都 610103；3.西南财经大学 统计学院，成都 610074）

0 引言

长期以来，宏观经济周期波动特征研究一直是学术界研究的重要领域，其主要集中在二个方面：一是经济周期波动非对称性，即经济扩张阶段与经济收缩阶段的不对称性，其主要的研究方法为Hamiltion(1989)的Markov机制转换模型；二是经济周期波动的协动性，即各种经济活动一起上升或一起下降，通常表现为宏观统计数据中的投资、消费、出口与就业等经济变量的同步变动，其主要的研究方法为Stock和Watson(1989)的动态因子模型。近来，Diebold、Rudebusch(1996)和Kim、Nelson(1999)分别利用多变量动态Markov机制转换的状态空间模型将经济周期波动的非对称性与协动性融合一起分析研究，更好地反应经济周期波动特征，为经济周期波动特征的实证研究开辟了新的研究方法。

本文利用多变量动态的Markov机制转换的状态空间模型，结合中国1992第1季度至2009年第2季度的宏观季度数据对中国经济周期波动的非对性与协动性融合一起进行分析研究，进而揭示出中国经济周期波动的特征与运行规律。

1 模型的设定

本文利用多变量动态Markov机制转换的状态空间模型对我国经济周期波动的协动性与非对称性进行分析研究，并构建出我国经济周期的计量模型。其模型由下列几个公式构成：

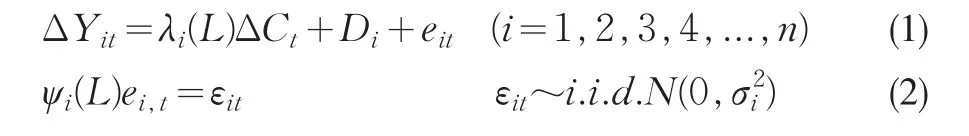
ΔYit(i=1,2,3,4,...,n)为第i个经济变量自然对数的一阶差分，即该经济变量的增长率，λi(L)、ψi(L)与ϕ(L)为滞后算子多项式。ΔCt为同步指数的增长率，为ΔYit的公因子成分，即各经济变量增长率的非观测共同因子成分。Di+eit为第i宏观指标的异质成分，其中Di为常数，eit为随机变量。wt为扰动项且假定与εit相互独立，δ为常数且决定同步指数的长期增长率，μSt为当经济处于扩张状态或收缩状态时，同步指数增长率偏离其长期增长率的程度。St为状态转换变量，当St＝0时，表明经济处于收缩状态；当St＝1时，表明经济处于扩张状态。St的转移概率矩阵为：

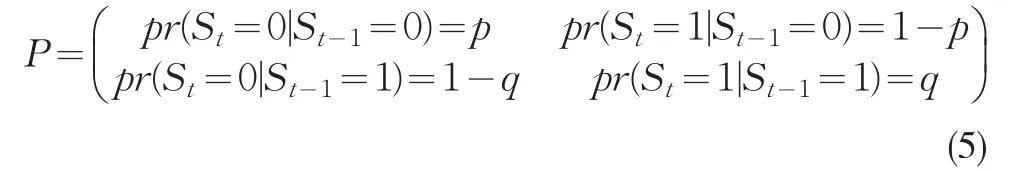
其中，p为收缩转换概率，即经济前期处于收缩状态时，当期仍处于收缩状态的概率，经济处于收缩状态的平均持续期为1/(1-p)；q为扩张转换概率，即经济前期处于扩张状态时，当前仍处于扩张状态的概率，经济处于扩张状态的平均持续期为1/(1-q)。

有（1）式，我们可以得出下列公式：

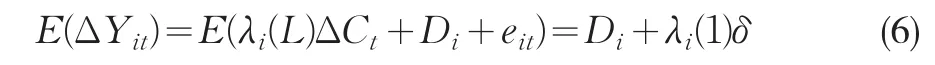
由于上式（6）中的参数Di，i=1,2,3,4,...,n,和δ过参数化，使得上述模型无法识别，因此，我们需要对各经济变量进行标准化处理。设 Δyit=(ΔYit-ΔYˉit)/std(ΔYit-ΔYˉit)，其中，ΔYˉit为 ΔYit的均值，std(ΔYit-ΔYˉit)为(ΔYit-ΔYˉit)的标准差。则上述模型中的（1）式和（3）式变为：

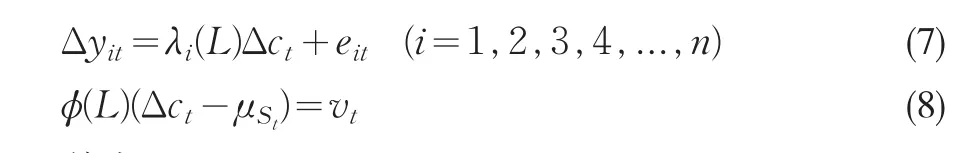
其中，Δct=ΔCt-δ。

2 数据及实证分析

2.1 数据

多变量动态Markov机制转换的状态空间模型对经济周期的非对称性与协动性的分析，首先需要选取一组宏观经济指标，选取的指标要相互独立且具有一定的代表性。由于投资、消费和出口是拉动经济增长的“三架马车”，就业对经济增长起着至关重要的作用，为此，本文选取了固定资产投资完成额、社会消费品零售总额、出口额和城镇单位从业人员数的季度数据①数据来源于中经网（www.cei.gov.cn），分别从投资、消费、出口、就业四个方面反映经济领域的变动情况。样本期为1992年第1季度到2009年第2季度，共70个样本数据，并利用1995年为基期的不变价格剔除价格影响因素。由于原始数据为季度数据，为此采用Census X-12方法进行了季节调整，以剔除掉季节因素和不规则成分。

2.2 实证分析

对于模型中的滞后算子，即λi(L)、ψi(L)（i=1,2,3,4）和ϕ(L)的确定，由于我们的样本量较为有限且根据目前已有研究的通常做法，我们假定ψi(L)和ϕ(L)为二阶滞后，即ψi(L)=1-ψi1L-ψi2L2（i=1,2,3,4）和ϕ(L)=1-ϕ1L-ϕ2L2。对于λi(L)，就固定资产投资完成额、社会消费品零售总额和出口额方程而言，我们假设λi(L)=λi（i=1,2,3），而城镇单位从业人员数，由于劳动力市场刚性，就业人数变化往往要略滞后于非观测共同因素的变化(Stock and Watson，1989），所以我们假设λi(L)=λ4+λ41L+λ42L2+λ43L3（i=4）。由此，我们可以将上述模型用下面状态空间的形式表示出来。

（1）测量方程：

（Δyt=HStβt+et）其中，y*it=yit-φi1yi,t-1-φi2yi,t-2,(i=1,2,3,4)；λ*41=-λ4φ41+λ41；λ*42=-λ4φ42-λ41φ41+λ42；

λ*43=-λ41φ42-λ42φ41+λ43；λ*44=-λ42φ42-λ43φ41；λ*45=-λ43φ42。（2）状态方程：

其中，ϕ(L)μSt=μSt-ϕ1μSt-1-ϕ2μSt-2。

将固定资产投资完成额、社会消费品零售总额、出口额和城镇单位从业人员数的季度数据分别代入上述模型，使用的是GAUSS9.0计量软件，采用Gibbs抽样方法对模型中的未知参数进行估计，具体计算时，我们共进行了10000次抽样，为了提高估计的准确度，我们舍弃了前2000次抽样结果，只取最后8000次抽样结果，最终的参数估计结果见表1。从表1中我们可以看出，各参数的估计均值均落在95%的后验概率区间,这说明所有参数的估计是可靠的，模型估计的整体效果很好，充分支持了我们前面对模型的设定。

从表1中的紧缩转换概率p＝0.5069,由此可得，从1992年第1季度到2009年第2季度，我国经济处于紧缩状态的平均持续时间为1/(1-p)＝2.028个季度；扩张转换概率q＝0.4799，由此可得，在此期间，我国经济处于扩张状态的平均持续时间为1/(1-q)＝1.923个季度。经济处于紧缩状态的平均持续时间要略低于经济处于扩张状态的平均持续时间。经济紧缩转换概率要略小于经济扩张转换概率，表明此期间我国经济波动产生扩张效应的可能性要小于产生经济收缩效应的可能性。δ＝0.0293表明，在此期间，我国经济同步指数每个季度以0.0293%的速度增长。μ0＝-0.2300表明经济处于紧缩状态时，同步指数增长率平均低于其长期增长率0.2300个百分点;μ0+μ1＝0.1371表明经济处于扩张状态时，同步指数增长率平均高于其长期增长率的0.1371个百分点。但从μ0和μ0+μ1的标准差可以看出，μ0和μ0+μ1不为零在统计上并不显著。这意味着，在此期间，我国经济周期的变化并不能明显地分为两个过程，即经济周期拐点处并不存在明显的机制转换。

表1 模型参数估计结果

图1 我国经济处于紧缩状态的概率

图2 我国经济同步指数的趋势变化图

在模型参数估计的基础上，我们可以推导出我国经济处于紧缩状态的概率图1和我国经济同步指数的趋势变化图2。从图1,我们可以看出，1993年第2季度到2009年第2季度，我国经济处于紧缩状态的概率基本上都在0.45～0.55的区间内变化，这表明在此期间，我国宏观经济整体运行较为平稳，波动性不大。在此期间，我国经济周期的处于扩张状态与紧缩状态的时期及其我国经济周期的拐点分布情况(见表2)。

表2 1993年第2季度至2009年第2季度我国经济周期的划分及其拐点

1992年以来，我国经济周期波动呈现上述特征的主要原因是：1992年以后，随着我国市场经济地位的确立，改革力度进一步加大，使得经济快速增长。之后，政府为了防止经济过热，采取了一系列紧缩的政策，使得我国经济在1996年以后实现了“软着陆”。1997年以后，我国政府为了应对亚洲金融危机给我国带来的经济不景气的影响，出台了一系列积极的财政政策，使得我国经济于2004年第1季度步入扩张阶段，持续到2008年第1季度。由于近来我国受到美国次债危机的影响，出口大量减少，使得我国经济从2008年第2季度步入紧缩状态，且下一个扩张状态的拐点到目前为止并未出现。

3 结论

通过上述对我国经济周期波动的协动性与非对称性的分析，我们可以得出以下主要结论：

（1）1992年以来，我国经济周期波动的协动性显著，非对称性不明显，经济总体运行较为平稳。我国经济周期波动呈现此类特征与运行特点主要是由于我国政府宏观调控政策的运用日趋合理，经济波动克服了过去反复出现的“大起大落”而进入相对平稳的增长态势。

（2）当前我国经济仍处于收缩状态，扩张状态的拐点并未出现，经济周期波动呈现此类特征为政府宏观调控政策的制度给予重要的启示，对提高宏观调控政策的针对性和有效性意义重大。目前，中国深受世界经济危机的影响，使得我国出口大量减少。出口在拉动经济增长作用减弱的情况下，政府应在投资与消费的“二架马车”上下功夫，加大投资力度，努力提高居民的消费水平，用投资和消费来推动经济的增长。把扩大国内有效需求特别是消费需求作为经济增长的基本立足点。

[1] Diebold,F.X.,G.Rudebusch.Measuring Business Cycles:A Model Per⁃spective[J].The Review of Economics and Statistics,1996,(78).

[2] Hamilton,James D.A New Approach to the Economic Analysis of Non⁃stationary Time Series and Business Cycle[J].Econometrical,1989,(57).

[3] Hamilton,James D.Time Series Analysis[M].New Jersey:Princeton University Press,1994.

[4] Kim,Chang-Jin.Dynamic Linear Models with Markov-switching[J].Journal of Econometrics,1994,(60).

[5] Kim,C.,Nelson,C.R.State Space Models with Markov Switching-Classical and Gibbs Sampling Approach with Applications[M].Massa⁃chusetts:MIT Press,1999.

[6] Lam,Pok-sang.The Hamilton Model with a General Autoregressive Component:Estimation and Comparison with other Models of Econom⁃ic Time Series[J].Journal of Monetary Economic Review,1990,(26).

[7] Stock.J.H.,M.W.Waston.New Indexes of Coincident and Leading Eco⁃nomic Indicators[A].In O.Blanchard and Fischer(eds.).NEBR Macro⁃economics,Annual[M].Cambridge,MA:MIT Press,1989.

[8] 郭庆旺,贾俊雪,杨运杰.中国经济周期运行特点及拐点识别分析[J].财贸经济,2007,(6).

[9] 刘金全,范剑青.中国经济周期的非对称性和相关性研究[J].经济研究,2001,(5).

[10] 钟伟,覃东海.商业周期理论的协动性和非对性综述.世界经济,2003,(1).