季节系数调整下的零售业销售总额预测方法

靳 惠

（河南财经政法大学，郑州450002）

0 引言

零售业在实现社会资源配置、生产者与消费者衔接、宣传文化要素等方面发挥了重大作用，一些大宗的零售品销售（如服装、食物，化妆品）具有很强的季节性特征，从零售业上市公司的财务年报中可以清楚的发现一般来说在前3个季度资金流较为充裕，在4季度初期会呈现出淡季特征，但到4季度末由于春节、元旦传统佳节的来临商业销售旺季到来。不同于制造业、农业，零售业这种内生波动+季节波动的双重波动给预测工作带来很大难度。单变量和多变量的计量回归模型在季节性经济现象中的作用大大折扣，如在一段时间的广告宣传和促销后，预测销售额成为未来企业战略制定的基础，但零售品所面临的顾客群体层次不齐，从顾客满意度、宏观景气角度进行的预测结果与实际不符。目前要做的是将以往的零售额数据中的季节因素剔除，计算出稳定趋势；同时根据得出的季节系数再进行返回预测。目前关于趋势剥离的数理方法很多，如HP滤波、BP滤波、卡尔曼滤波，以及最先进的小波理论等等。目前关于季节性调整的方法主要有Census X12，韩荆（2009）运用Census X12季节调整法与HP滤波法对吉林现金投放数据序列进行分离并得到相关结果。针对零售品销售额的预测研究成果也比较多，如秦伟良（2008）以状态空间和卡尔曼滤波结合，构建预测模型；刘家琨（2011）时间序列季节模型和单整自回归移动平均(ARIMA)模型,对福建省的消费品零售总额进行预测。何光优（2010）使用稀疏系数法的SARIMA模型对中国消费品零售总额进行预测。周坤乔（2005）使用多种差异模型进行预测并比对结果，意图找出最佳方法。笔者认为：在各模型当中并无最优之说，即使某种方法在一个时期内预测误差最低也不能保证在市场机制和规律发生变化时也同样适用。大多数预测者使用的是自回归向量模型，如李智勇（2006）等。以苏果连锁、苏宁电器为代表的江苏零售企业在市场经济中不断壮大，在总结归纳相关数理方法之后，依据季节处理方法对销售额序列进行稳定趋势和季节效应的分离，计算出季节系数，随后对稳定趋势进行预测并还原，结果显示预测误差较小。

1 零售业销售总额预测：以江苏为例

在进行实际预测之前，需要对具体预测步骤进行一个详细的说明，如图1。

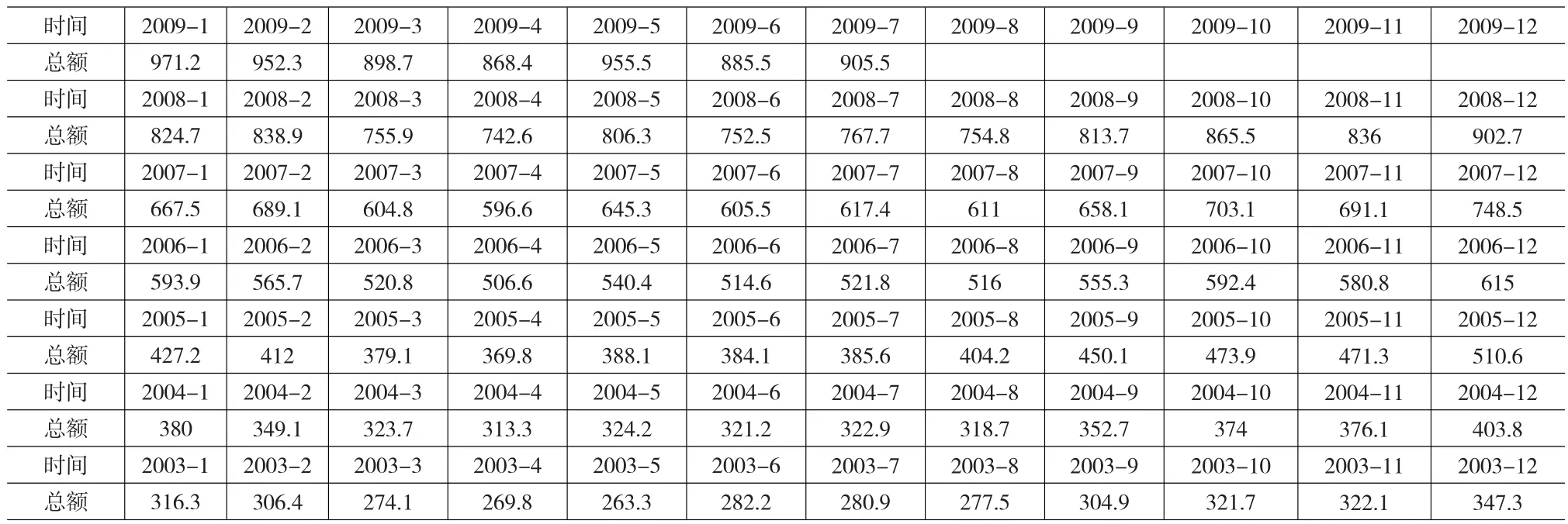
表1 原始数据(单位：亿元)

1.1 江苏零售品销售总额的统计分析

季节调整的前提在于数据具有季节变动特征，决定了其数据结构应以4为一个阶段，如1年中的4个季度、4年和4个10天等。按照调整规则，调整的极大样本数量为240个。本文的数据来源于江苏省统计局网站（http://www.jssb.gov.cn），数据选取段为2003年1月～2009年7月份，共计79个。（见表1）

EVIEWS5.0软件为专业统计和时间序列处理软件，根据其VIEWS板块功能进行表1数据绘图得到图2。江苏省社会零售品销售额从2003年的316.3亿元增长到了2009年7月的905.5亿元，翻了整整3倍。上涨趋势明显，而且每年的数据规律为正U型即销售额先将后涨，具有明显的季节性特征。

1.2 稳定趋势分析

图2 零售总额原始序列

图3 稳定趋势序列

时间序列中的长期趋势为一种内在的、不可因为季节和随机扰动就能够改变整体趋势的内在现象。零售额上涨是由社会生产力的提高和人民消费观念和认知的改变以及购买力的增强所决定的，如果我们将图1中2003年1月和2009年7月的两个数据点连接起来会形成一条直线，那么实际序列是围绕这条线波动的，这条线类似于稳定趋势线，根据EVIEWS中的X12模块功能，得到表2中的稳定趋势数据。

图3是分离出的稳定趋势曲线，除了2006和2008年等奇异点外近似为一条直线，说明江苏消费者的消费能力增长比较稳定。出现小幅波动的原因在于预防性动机，当人们手中财富总量不变在一定时期需要花费大量的金钱时，总会在其他一段时间相对节约，故在11月左右人们为了即将到来的春节做准备将会下意识的去积累财富。在零售企业做销售策划时应当注意到这一点。

表2 稳定趋势数据 （单位：亿元）

1.3 季节系数的测算

总趋势是长期趋势、循环因素、季节因素和随机扰动因素共同决定的，但从上文的分析来看，循环因素和随机扰动因素基本不存在。同时分离有两种，一种是加法原则，一种是乘法原则。这里采用乘法原则，即总趋势为长期趋势和季节因素的乘积，Y=S*TC。由于篇幅限制，季节因素序列的数据表省略，由图4表示。得到江苏零售品总额序列遵循季节性波动明显且在各年基本一样，从年初开始下降至4月份，后到5月有细微上升，后至7月份下降，随后到10月份逐渐上升，在11月有个缓冲后再上升到顶点。值得说明的是在原始数据中有个别数据缺失，采取插值法补全。季节调整的公式为，这是下面进行零售消费额的预测基础。一些日用的商品，如冷饮、空调和冬夏服装等淡旺季明显，故季节系数的测算至关重要。季节系数测算结果如表3。

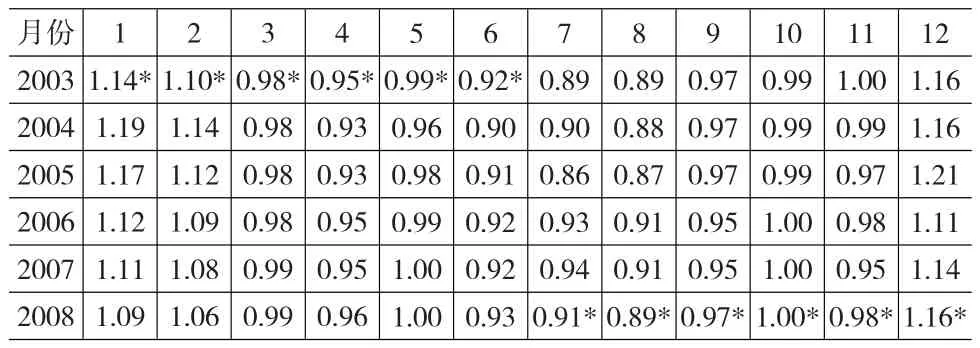
表3 季节系数

1.4 季节调整下的预测

根据上文的数据序列分离得到了稳定趋势和季节因素，图3和图4两个序列。首先对稳定趋势进行单回归计量方程预测，后根据季节系数进行预测值还原。

（1）以时间t为自变量的稳定趋势预测

回归方程表述为：

通过OLS最小二乘回归结果如下：

结论显示在无其他特殊情况（税收制度及宏观环境的变动）下，江苏零售业销售总额随着时间的推移每过一个月将增加8.546亿元。对2009年1～12月的预测结果如表4。

（2）根据季节系数对预测结果还原运用预测得到的TC序列与季节指数S相乘，即

表4 稳定趋势预测结果 (单位：亿元)

Y^=Ct×S，得到Y的预测结果。

1.5 预测结果有效性检验及新的预测

图1 季节调整下预测的步骤

图4 季节因素序列

在众多预测方法共存的前提下，预测方法的有效性应当通过误差来判定。这里简单的将考察期内原始序列和还原序列的和计算出来为6437.1亿元和5934.9亿元，预测误差为8.47%。进一步使用SPSS软件中的配对检测板块对两组数据是否存在显著差异进行判定，根据相等性检验结果，两序列波动存在共性，即序列方差无显著差异。同时各检验指标通过检验，显著性P值超过预定标准，接受两序列无明显差异的原假设。根据误差8.47%，进行预测值还原，公式为Y×(1+8.47%)，结果为 853.8、939.5、977.9、968.1、1155.7亿元。

表5 还原结果 单位：亿元

表5 预测结果有效性检验

图5 原始序列与还原序列图

2 结论

本文根据季节调整方法对江苏零售品销售总额进行趋势分离后得到季节修正系数，对趋势序列进行预测后并进行还原，最后实现了误差检验。经过研究有以下结论。一是整体上看江苏零售品销售额整体上为稳定上升趋势，呈先下后上的明显U型状，循环因素和随机扰动作用不显著，受强季节因素影响。二是预测效果良好，还原序列与真实序列的配对检验显示两序列没有明显差异，这个预测方法在其他省份的零售品销售额预测同样适用。江苏在制定零售品产业发展规划时应当注意到季节因素的影响。

[1] 韩荆.基于Census X12与HP滤波下的现金投放分析[J].工业技术经济，2009,（10）.

[2] 刘家琨，徐学荣.福建省社会消费品零售总额的预测[J].福建农林大学学报(哲学社会科学版),2011,（3）.

[3] 何光优，田应福.中国消费品零售总额序列的SARIMA模型及其预测技巧[J].经济研究导刊，2010,（19）.

[4] 周坤乔.社会消费品零售总额实际预测方法的探讨[J].浙江统计，2005（8）.

[5] 李智勇.ARIMA模型在批发和零售贸易餐饮业预测中的应用[J].北京市财贸管理干部学院学报，2006,（3）.

[6] 秦伟良.姚如一.基于状态空间建模法的社会消费品零售总额预测[J].统计与决策，2008,（10）.

[7] Chang,Ha-Joon,Park,Hong-Jae,Chul Gyue Yoo.Interpreting the Ko⁃rean Crisis“Financial Liberalisation,Industrial Policy and Corporate Governance”[J].Cambridge Journal of Economics,1998,(22).

[8] 大洋新闻网.全球零售业前景好国企大胆出国门[RB/OL].http://gz⁃daily.dayoo.com/gb/content/2003-05/12/content_1061694.htm，2011-8-16.