水下多智能体系统快速编队控制

李德远，佘莹莹

(1．海军驻葫芦岛431厂军事代表室，辽宁 葫芦岛 125004 2．武汉第二船舶设计研究所，湖北 武汉 430074)

水下多智能体系统快速编队控制

李德远1，佘莹莹2

(1．海军驻葫芦岛431厂军事代表室，辽宁 葫芦岛 125004 2．武汉第二船舶设计研究所，湖北 武汉 430074)

针对水下多智能体系统在无向网络下的快速编队问题，提出基于智能体当前和过去状态的快速编队控制算法。利用矩阵理论和频域分析法，得到该算法能使系统快速编队的过去状态区间。仿真示例验证了其有效性。

水下多智能体系统;编队控制;收敛速度

0 引言

近年来，由于海底环境复杂多变，很多工作都不适合潜水员及载人潜水器进行。作为海洋资源开发工具，水下智能体(AUV)成为当今各国在海洋工程领域中的研究热点。这主要是由于在实际的水下作业中，AUV可以自主地运行在远程的、难于接近的、无法预知的或危险的海洋环境之中，完成自主导航、自主避障和自主作业等任务。

基于水下智能体系统的广泛工程应用，其编队控制问题引起了控制领域的极大关注。编队控制［1－2］要求系统中的个体共同保持一个设定的几何图形。在分布式编队的稳定性问题中，每个个体都知道最终的队形，但个体间需要进行通讯来协调各自的位置。这个问题的信息状态包含了队形的中心位置信息，个体间可以使用一致性算法来得到队形的中心位置信息。

本文主要研究了AUV群的快速编队控制问题，目前已有的编队控制算法主要是基于当前状态的，但对于任何控制系统而言，过去的状态都值得考虑，而且很容易得到，本文提出的快速编队控制算法不仅利用智能体当前状态，还利用智能体过去状态的相关信息，在不需改变网络拓扑结构的情况下，所提出的算法可有效提高系统的编队速度。

1 预备知识

假设水下多智能体系统中有n个智能体，用1个无向图G=(V，E，A)来表示智能体之间的信息交换网络拓扑结构。顶点集V={v1，v2，…，vn}为有限的非空集，图的顶点vi表示智能体i;边集E⊆V2，图的边eij=(vi，vj)∈E表示智能体i和智能体j可以相互传递信息，即eij∈E⇔eji∈E;加权图的邻接矩阵A=［aij］为对称非负矩阵。其中，aii=0，当i≠j且(vi，vj)∈E 时，aij＞0。智能体i的邻接成员用集合Ni={vj∈V：(vi，vj)∈E}表示。

如果图G中2个不同顶点vi和vj存在1条路径时，称vi和vj可达。当且仅当图G的任意2个不同顶点之间都存在一条路径时，称该图是连通图。

定义1 无向图G的Laplacian矩阵定义为

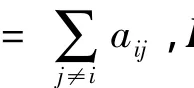
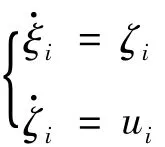
可以比使用标准算法

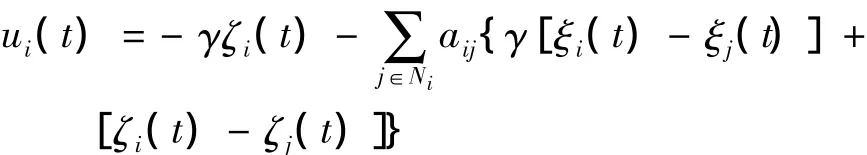
更快达到静态一致，且满足

2 水下多智能体系统快速编队控制

考虑具有n个智能体的多智能体系统，其中每个智能体的动态模型为：

其中：ri∈R2，vi∈R2，ui∈R2分别表示智能体 i的位置，速度和控制输入。

为了使系统满足ri－rj→Δij和vi→vj→vd(t)，其中vd(t)为队列的前行速度，Δij为智能体i和为j的相对距离。令εi∈R2为常数，并且满足ri－εi→rj－ εj和vi－ vj→vd(t)，即：ri－ rj→ εi－ εj和vivj→vd(t)。因此，可以选择合适的εi来满足智能体之间的相对距离。根据传统的动态一致性算法得到的编队控制算法为

所提出的快速编队控制算法为

定理1 考虑具有n个水下智能体系统，其通信拓扑结构图G为连通图的情况，当θ∈(0，σ)时，系统(1)使用快速编队控制算法(3)可以比使用编队控制算法(2)更快达到所要求队形。其中σ满足：

证明：定义

则系统(1)使用快速编队控制算法(3)时可转换为：

可以得到：

同样，根据式(5)，系统(1)使用编队控制算法(2)可以转换为：

由引理1可知，当θ∈(0，σ)，且σ满足(4)时，系统(6)比系统(7)更快达到静态一致，即系统(1)使用快速编队控制算法(3)可以比使用编队控制算法(2)更快达到所要求的队形。

3 仿真算例

考虑由4个水下智能体组成的系统，其通信网络拓扑结构图的Laplacian矩阵为

此时L矩阵的特征值为λ1=0，λ2=0.443 4，λ3=1.241 0，λ4=1.715 6。由定理1得到，当θ＜ 6.8 s时，系统(1)可以实现快速编队控制。要求的队形如图1所示，可以得出(3)中的=［0，0］T，=［1，0］T，要求队列的前行速度为vd(t)= ［sint，cost］T。对于1组随机给定的初始状态，选取γ=1，图2和图4分别是系统使用编队控制算法(2)时的运动轨迹以及位置和速度信息;图3和图5分别是θ=2 s时，系统使用快速编队控制算法(3)时的运动轨迹以及位置和速度信息。

通过仿真图看出，当网络拓扑结构和θ满足定理1的条件时，水下多智能体系统可以快速编队。

4 结语

本文提出一类基于智能体当前状态和过去状态的编队控制算法，有效地解决了具有2次积分动态的水下多智能体系统的快速编队问题。与标准算法相比，所提出的算法通过利用控制系统中更多有效信息，来确定智能体的下一步状态。通过分析得到，在给定条件下，水下智能体能快速达到预定的速度，并且可以快速形成任意给定的队形。

［1］SHE Ying-ying，FANG Hua-jing．Fast distributed consensus control for second-order multi-agent systems［A］．The 23th Chinese Control and Decision Conference［C］．Xuzhou，China，2010，5：87－92．

［2］杨波，方华京．分布式控制框架实现水下航行器群协调控制［J］．华中科技大学学报，2008，36(12)：39－42．

Fast formation control for underwater multi-agent systems

LI De-yuan1，SHE Ying-ying2
(1．The Navy Delegationin No．431 Shipyard，Huludao 125004，China;2．Wuhan Second Ship Design and Research Institute，Wuhan 430064，China)

For underwater multi-agent systems a fast formation control protocol uses both current states and outdated states is proposed．The fast formation control prototocl is analyzed under a undirected communication graph．Based on the frequently-domain analysis and matrix theory，it is shown that the system use the fast formation control protocol formation faster than use the standard formation control protocol if the outdated states are chosen properly．Simulation results illustrate the correctness of the result．

underwater multi-agent systems;formation control;convergance rate

TP13

A

1672－7649(2012)05－0067－03

10.3404/j.issn.1672－7649.2012.05.015

2011－05－05;

2012－04－18

李德远(1965－)，男，高级工程师，从事船舶系统技术研究。