基于BP神经网络光伏发电系统MPPT的研究

梁惺彦，张 蔚

（1. 南通大学 计算机科学与技术学院，南通 226019；2. 南通大学 电气工程学院，南通 226019）

0 引言

随着世界经济的发展和人口数量的不断增长，人们对于能源的需求越来越大，一次能源的消耗过程中所带来的环境污染问题已越来越严重。因此，清洁的可再生的太阳能越来越受到人们的重视。但由于光伏电池的转换效率较低，且价格较高，严重阻碍了光伏发电系统的推广和应用，因此必须最大限度的利用光伏电池所产生的功率，以降低光伏发电的成本。

目前常用的最大功率点跟踪的方法有模糊控制法、扰动观察法、电导增量法等[1～4]，这些方法存在控制复杂、难于实现、扰动量无法确定等问题。本文根据影响光伏电池输出功率大小的温度、光照、阴影等外界条件设计BP神经网络，通过实验所测的数据进行训练，预测出光伏电池的最大功率点电压，进而进行MPPT控制，提高了系统的控制效率和精度。

1 光伏电池模型及输出特性

1.1 光伏电池模型

光伏电池是利用太阳能的光伏效应，将光能转换为电能的一种转换装置。光伏电池的等效模型如图1所示。它由1个电流源、1个二极管、1个高阻抗电阻Rsh、1个低阻抗电阻Rs和1个负载电阻R组成。

其中，光伏电池的输出特性方程为：

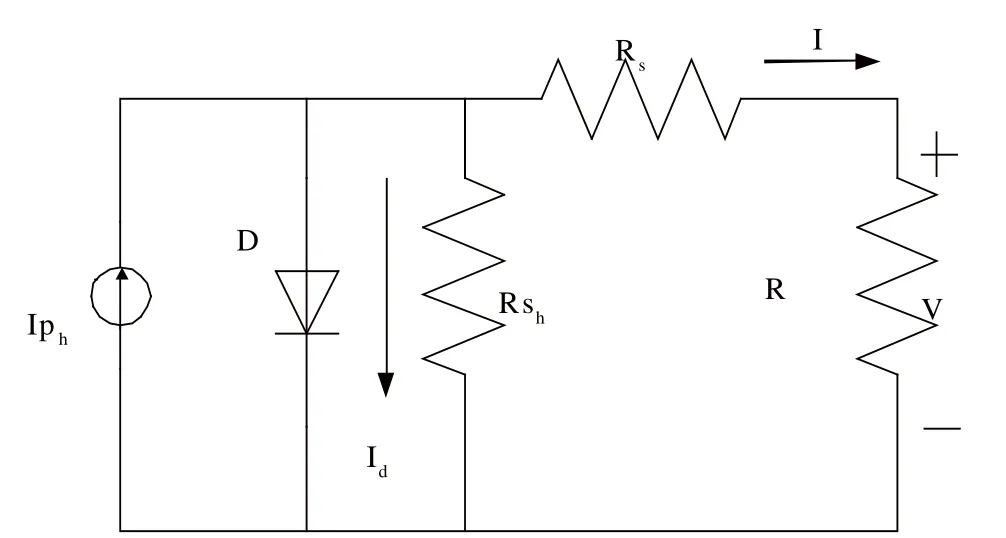
图1 光伏电池等效模型

式中：

I、U 为光伏电池输出电流和输出电压；

I0为光伏电池暗饱和电流；

Iph为光电流；

q为 单位电荷；

A为二极管品质因子；

K为玻尔兹曼常数；

T为光伏电池的表面温度；

Ior为参考温度 下的暗饱和电流；

Tr为参考温度；

EG为硅的禁宽温度；

Isci为标准测试条件下光伏电池的短路电流；

Ki为短路电流的温度系数；

S为日照强度。

1.2 光伏电池输出特性

光伏电池的发电原理可知，光伏电池是一种非线性直流源，它的输出特性受到光强与温度外界因素的影响。如图2（a）所示，当光强恒定时，温度从5℃逐渐增加时光伏电池的输出特性，由图可知开路电压逐渐减小，最大功率点也逐渐减小；如图2（b）所示，当温度恒定，光照强度S从1kw/m2逐渐减小，光伏电池开路电压略为减小，最大功率点电压基本不变，输出的最大功率逐渐减小。

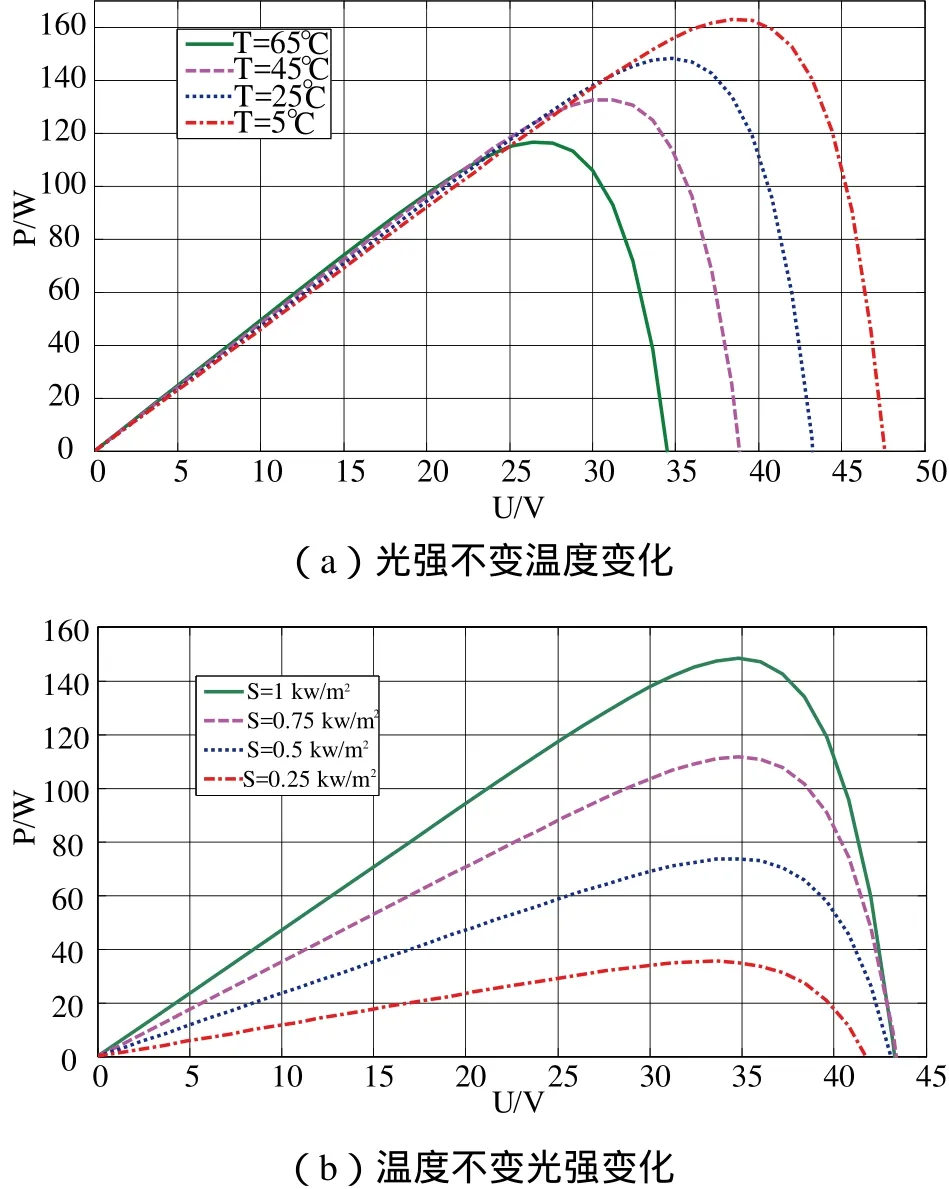
图2 光伏电池输出特性

光伏电池作为太阳能光伏发电系统的基本发电单元，容易受到周围建筑物、树木和电线杆以及天空中乌云等的影响，局部阴影对光伏电池的输出特性影响如图3所示。从图中可知随着遮挡比例的增大最大功率点减小，阴影对于光伏电池的输出特性有着明显的影响。

因此，当外界因素发生变化时，光伏电池很难保证最大功率的输出，从而造成能源上的浪费。为了提高光伏电池的转换效率，就需要跟踪光伏电池的最大功率点。

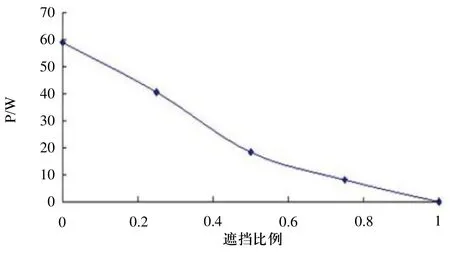
图3 局部阴影对光伏电池输出特性的影响

2 MPPT的BP神经网络设计

2.1 BP神经网络

BP算法是目前比较流行的神经网络学习算法，是能实现映射变换的前馈型网络中最常用的一种网络算法，是一种典型的误差修正方法，属于“逆推”学习算法。BP神经网络主要由三部分组成，分别为：输入层、隐含层、输出层，同层结点之间没有连接，层间结点实行全连接，每层结点的输出只影响下一层结点的输出，如图4所示。

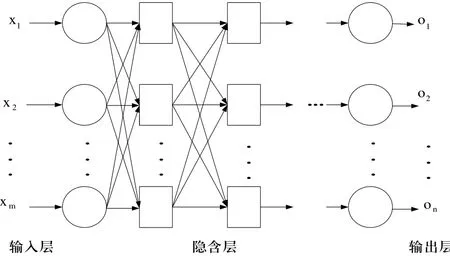
图4 BP神经网络结构

2.2 BP神经网络设计

1）输入层设计

输入层的个数由解决问题和数据表示方式确定。对于光伏系统中最大功率跟踪，影响因素为光照强度、温度、局部阴影，另外还要综合考虑时间的因素，因此输入层需要四维输入，输入层传输函数采用tansig型。

2）输出层设计

输出层的维度根据使用者的要求决定。本文设计输出层为1，即最大功率点电压，输出层传输函数采用logsig型。

3）隐含层设计

（1）隐含层数设计

研究表明当各节点均采用S型函数时，一个隐层就足以实现任意判决分类问题。增加隐层数可更进一步降低误差，提高精度，但同时也使网络复杂化，增加了网络权值的训练时间。而误差精度的提高也可以通过增加隐层中的神经元数目来获得，其训练效果也比增加隐层数更容易观察和调整。所以，在一般情况下，应先考虑增加隐层中的神经元数量，在单隐层不能满足要求时，可以考虑增加隐层数目[5]。因此本文采用单隐层。

（2）隐含层节点数设计

隐含层的节点数选择非常重要，它不仅对建立的神经网络模型的性能影响很大，而且是训练时出现“过拟合”的直接原因。为尽可能避免训练时出现“过拟合”现象，保证足够高的网络性能和泛化能力，确定隐含层节点数的最基本原则是：满足精度要求的前提下，尽可能紧凑结构，即取尽可能少的隐含层节点数。采用黄金分割法[6]确定隐含层节点数。隐含层节点数设计为6。因此，本文设计的BP神经网络结构如图5所示。

3 基于BP神经网络MPPT控制系统研究

3.1 MPPT的BP神经网络模型训练

本文针对无锡尚德公司生产的STP150S-24型号光伏电池板进行实验测试，采样一天24h中的光强、温度、阴影几组数据，通过如图5所设计的BP神经网络结构进行学习训练，最大训练次数为1000次，训练期望误差为0.001，训练步长为0.05，训练函数采用trainlm，训练结果如图6所示。

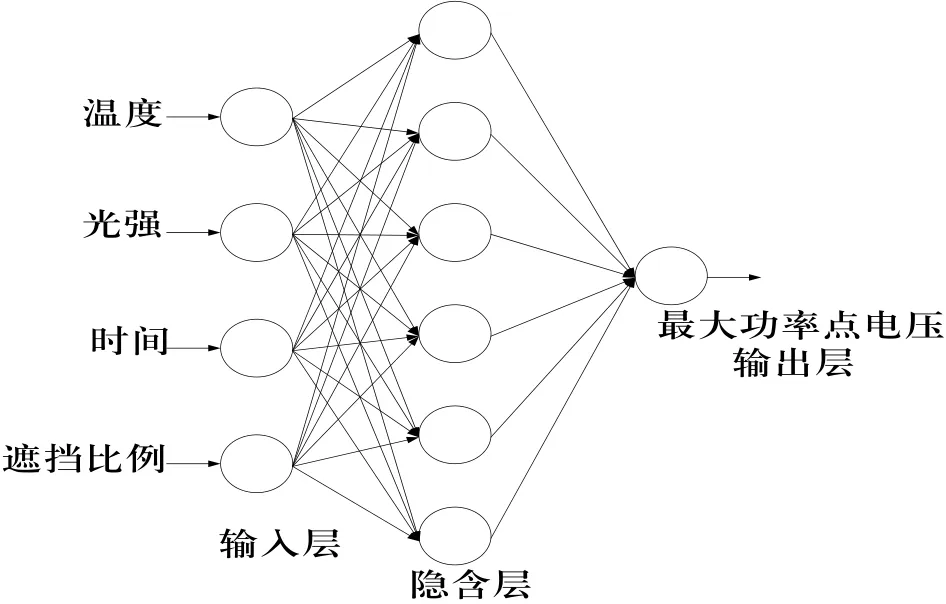
图5 MPPT的BP神经网络结构

图6 BP神经网络最大功率点预测图

从图中可知BP神经网络预测电压与实际最大功率点电压很接近，说明通过BP神经网络进行MPPT控制将会具有较好的控制精度。

3.2 光伏发电系统仿真模型

光伏发电系统仿真模型由光伏电池PV模块、DC/DC变换电路、PWM模块、MPPT模块组成（如图7所示）。

图7 光伏发电系统的仿真模型

系统参数设置：T=25℃， C=220uF，L=1.6mH，R=22Ω，不考虑阴影T1=0，开关频率10KHz，仿真时间t=0.1s，求解器选择ode23t，其中步长为0.001。

3.3 仿真结果

设置S在0.05s时从1000W/m2突变为800W/m2，仿真结果如图8所示。经过0.02s系统稳定在140W左右的最大功率点处，0.05s时光强发生改变，其他因素不变，在0.06s左右控制系统跟踪到新的最大功率点，稳定在115W左右。从仿真结果可以看出BP神经网络能快速跟踪到最大功率点，具有较好的控制性能。

图8 最大功率跟踪控制的仿真结果

4 结论

本文根据影响光伏电池输出特性的温度、光强、阴影外界环境因素设计了BP神经网络，对光伏发电系统进行最大功率跟踪控制，仿真实验表明该方法能快速跟踪光伏电池的最大功率点，有效适应外界环境变化，具有较好的控制精度和稳定性，并且由于该系统简化了光伏发电系统的硬件结构，具有较好的实际应用前景。

[1] N. Kasa, T. Iida. Flyback Inverter Controlled by Sensorless Current MPPT for Photovoltaic Power System. IEEE Trans.Ind. Electron, 2006, 52(4): 1145-1152.

[2] Yang Chen，Keyue Ma Smedley．A Cost-Effective Single-Stage Inverter With Maximum Power Point Tracking[J].IEEE Transactions On Power Electronics, 2004, 19(5):1289-1294.

[3] 张超, 何香凝. 非对称PID模糊控制在最大功率点跟踪中的应用[J]. 电工技术学报, 2005, 20 (10) : 73-75.

[4] 李炜, 朱新坚. 光伏系统最大功率点跟踪控制仿真模型[J]. 计算机仿真, 2006, 23(6): 239-243.

[5] 唐彬. 基于神经网络和支持向量机的光伏最大功率跟踪研究[D]. 广东: 汕头大学, 2008.

[6] 夏克文, 李昌彪, 沈钧毅. 前向神经网络隐含层节点数的一种优化算法[J].计算机科学, 2005, 32(10): 143-145.