基于模拟退火粒子群算法的钎焊炉调度优化

蔡志端，毛建华

（湖州师范学院 信息与工程学院，湖州 313000）

0 引言

钎焊炉是机械、冶金等行业零部件热处理加工中的重要设备，热处理设备能耗巨大[1,2]。对工业生产过程调度优化可降低能耗，提高生产效率，所采用的调度优化算法也获得了广泛的研究[3～5]。目前对钎焊炉的研究主要集中在炉内温度控制问题，而针对钎焊炉生产调度优化问题的研究没有涉及到。钎焊炉的生产调度水平影响着其生产加工的质量、产量和生产过程的能耗。钎焊炉生产过程能耗主要包括所耗电能及氮气量。

近年，智能搜索算法在解决调度优化问题成效显著[6]，主要有蚁群算法、遗传算法、模拟退火算法、粒子群算法等等。这些算法在调度优化问题求解中都有其各自优缺点。粒子群算法有概念简单、容易实现，快速收敛的优点，但其容易陷入局部最优，使得精度降低[7]。为弥补这一缺点，学者们进行了广泛的研究，其中，将粒子群优化算法（Parti- cle Swarm Optimization，PSO）与具有跳出局部最优能力的模拟退火算法（simulated annealing ,SA）相结合，提出模拟退火粒子群算法（SAPSO）改进系统性能，取得了较好的应用[8,9]。论文在借鉴前人研究成果基础上研究SAPSO在钎焊炉调度优化的具体应用，以达到良好的优化效果。论文在考虑降低钎焊炉生产能耗和提高生产效率下，建立了钎焊炉调度优化数学模型，并结合粒子群算法和模拟退火算法的优点，设计了求解模型的算法。

1 过程描述及建模

1.1 生产过程描述

在一般企业生产中，由于钎焊炉开炉温升阶段耗能大，周期长，所以钎焊炉常采取订单定期计划开炉，多品种分批次批量统一加工生产等方式，以保证企业利益最大化。钎焊炉生产工艺流程如图1所示，待加工的工件摆放至钎焊炉传送机带后，进入喷淋钎焊剂区对工件喷淋焊剂液，然后在空气吹落区吹落工件上多余的多钎焊剂，通过干燥区烘干钎焊剂和工件表面水分后再进入加热区[10]。工件在加热区要通过多个不同温度环境的加热段进行加热焊接。工件从加热区出来，最后进入冷却区进行水冷、风冷区进行冷却后取下，完成加工。由于企业常按订单定期计划开炉进行生产，在生产计划安排中，企业按订单所要求的加工产品的种类进行分类，将相同或相近的产品作为一类，统一加工。图中D1，D2，D3分别代表三个不同的工件类别。

从图1可知，每个加工工件都要经历5个加工单元，每一个加工单元又对应不同的加工设备。钎焊炉调度问题优化目标就是在确定的加工工件类别的基础上，合理设计不同类别工件的加工顺序使其在不同加工设备上的驻留时间最小，从而缩短全部产品的加工时间，降低能耗，提高生产效率。

图1 钎焊炉生产基本流程

钎焊炉调度过程，需要考虑以下七个约束条件1）待加工工件各类有i种，且都需要经历5个连续生产单元；2）第i类工件第j个工件在第m个生产单元中加工时开始加工的时间为Bijm，加工完成的时间为Eijm；3）工件加工最小时间，根据其种类不同都有其规定的加工时间及加工温度。每一类工件在每个加工单元驻留时间需要达到其在该单元满足加工工艺要求的最小驻留时间（该时间为已知），加工温度满足加工工艺要求，且每一类加工工件加工最小时间相同；4）每类工件在各个加工单元中按先进先出的顺序执行，只有当前一类加工工件离开加工单元时，新的工件才能进入；5）不考虑钎焊炉停机等待情况；6）每一个加工单元，同一时刻只能加工同一类工件；7）在加工初始时刻，任意一类工件都有可能被选择加工。

1.2 钎焊炉调度的数学模型

根据1.1节描述，可建立钎焊炉调度问题的数学模型，模型中主要的参数定义如下：

i：待加工工件类别编号，i=1,2,3,…；

Di：第i类待加工工件集合，设不同类别加工工件集合交集为空；

j：Di中待加工工件的编号，j=1,2,3,…,;

m：钎焊炉加工单元编号，m=1,2,3,4,5;

Hm：第m号加工单元可同时加工的工件数量；

Bijm：第i类第j个工件进入第m个加工单元的起始时间；

Eijm：第i类第j个工件加工完毕后离开第m个加工单元的时间；

STim：第i类工件在第m个加工单元中满足加工工艺需要的最小加工时间;

Tijm：第i类第j个工件在第m个加工单元驻留时间；

Φim：第i类工件在第m个加工单元中加工状态，为1表示在加工，为0表示不在加工；

δijm：第i类工件第j个工件在第m个加工单元中加工状态，为1表示在加工，为0表示不在加工；

基于上述定义，调度模型如下[5]：

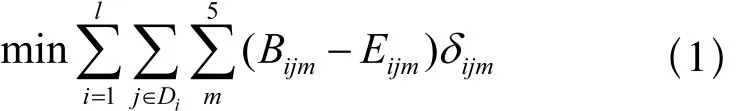
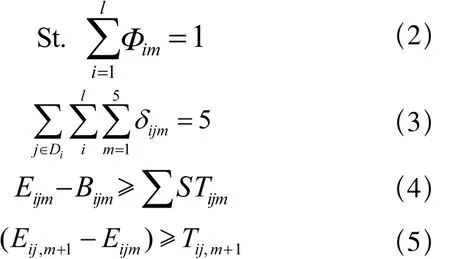
以上模型中，目标函数（1）表所示有待加工工件加工时间最小化；约束条件（2）表示每一次中能选择同一类加工工件进行加工；约束（3）表示每一件加工工件都可被选择到每个加工单元加工且只能选择一次；约束（4）表示每一个加工工件在某个加工单元的驻留时间不能小于额定最小加工时间； 约束（5）只有当前加工工件离开加工单元时，新的工件才能进入。

2 求解钎焊炉调度的SAPSO算法

PSO算法是一种模拟鸟群觅食行为的群体智能优化计算技术，是一种基于迭代的并行优化搜索工具[11]。在PSO算法中，设置一群“粒子”并将每个粒子看作是优化问题的一个可行解。被优化的函数确定每个“粒子”的适应度值，以此评价粒子的好坏。“粒子”根据自己的速度和位置变量计算其在可行解空间中运动的方向和距离；粒子将跟踪自身迄今为至找到的最优解和整个种群迄今为止至找到的最优解更新自己的位置与速度；通过多次迭代运算找到最终最优解。粒子i在第t次迭代的状态属性可由其位置与速度变量表示。位置变量表示为：别为搜索空间的下限及上限。速度变量表示为：别为粒子在可行解空间运动时速度的最小值与最大值。算法中粒子的速度和位置更新公式分别为

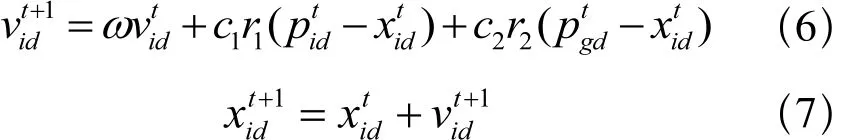
其中ω为惯性权重，合适的惯性权重可平衡全局搜索和局部搜索能力，实现在更少迭代次数下提高寻优性能，目前常采用线性策略、非线性策略两种ω调整策略；c1和c2为学习因子，它反映了粒子间信息交流强度，通过取 c1=c2∈ [1，2，5]；r1和r2为0到1之间均匀分布的随机数；Pid为个体最优位置；Pgd为全局最优值。

将模拟退火算法应用于PSO中粒子的速度和位置更新过程。PSO每次迭代中的适应度值根据模拟退火算法中的Metropolis准则按一定概率允许接收非优化解，使算法从局部极值区域中跳出，最终收敛于全局最优解，按下以步聚实现SAPSO算法，搜索最优解[12]：

1）参数初始化，包括粒子数m，惯性权重ω，迭代次数t，学习因子c1和c2,搜索空间的下限及上退火速度α，随机设置粒子的位置初始值xi(t)和速度初始值Vi(t)，个体最优值pid和全局最优值pgd；

2）根据被优化的函数及其约束条件，计算每个粒子的适应度值f ()，并分别与个体最优值和全局最优值比较，选择更优值，以对pid和pgd进行更新；

3 实验与结果分析

3.1 粒子编码与适应度函数

SAPSO应用于钎焊炉调度，首先要建立位置矢量与调度方案之间的映射，即寻找一种表达方式，使粒子与解对应。考虑到钎焊炉加工过程是流水作业，同一加工单元只加工同类别的工件，且待加工工件数量，加工单元最大加工数量和最小加工时间已知。对粒子采用矩阵编码[13]，如下所示：

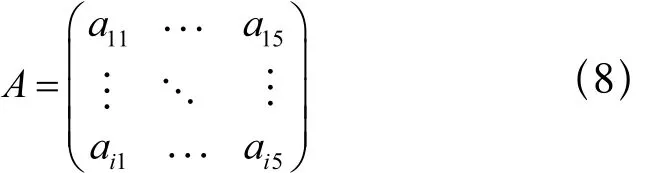
矩阵A是所有待加工工件对应5个加工单元的编码。矩阵中每一个元素值aij表示第i个工件在第j个加工单元中加工的顺序号，为一整数。A矩阵每一行为某一类中某个工件在各加工单元加工顺序，每一列对应着一个加工单元。由于钎焊炉各加工单元是流水线作业，故矩阵A中每一列的数值就代表所有工件加工的顺序，且对于同一行，各列的值相等。解码时，提取矩阵A中的任何一列的数值，其值表示元件加工顺序。在搜索矩阵A最优值时，从第二个生产单元开始，必须考虑工件在前后两个个生产单元的最小加工时间差，将该时间差与工件加工顺序相结合。由于各工件在某加工单元标准加工时间确定，所有待加工工件在各加工单元的标准加工时间表示为：

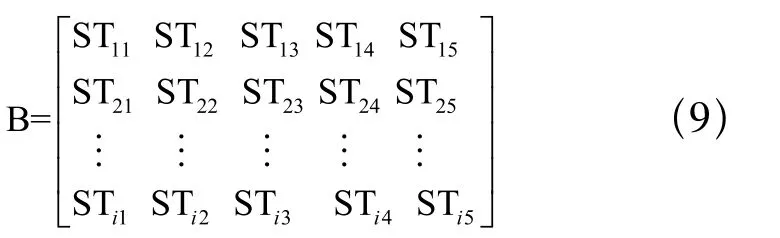
其中，STim表示第i个加工工件在第m个加工单元上的标准加工时间。则所有待加工工件在加工过程中，相邻两个加工单元加工时间差总和可表示为：

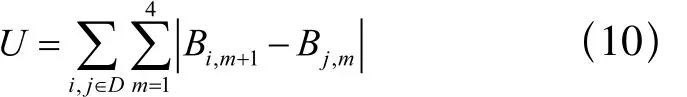
调度优化则可转换成求U的最小极值。对于调度数学模型中的约束项，可在目标函数中增加一项可以映射约束条件的惩罚像，构成一个无约束的广义目标函数。因此论文中钎焊炉调度优化的适应度函数即转换成是一种对B矩阵排序的问题。

3.2 实验结果

将论文中的算法应用于钎焊炉调度优化。算法中主要参数进行适当设置：最大迭代次数为800，群体粒子数为50；学习因子C1和C2取1.8，惯性权重ω∈[0.9, 0.4]，

模拟退火中退火起至温度T和T0分别取8000和0.03，退火速度α取0.9。采用某企业钎焊炉加工工件数据进行仿真实验，针对不同批次数据分别按标准PSO算法和SAPSO算法仿真，并与无调度优化前加工时间进行对比，结果如表1所示。

表1结果表明SAPSO算法达到优化目的。当工件类别量多，加工时间较长时，SAPSO算法比标准PSO算法效果更好。

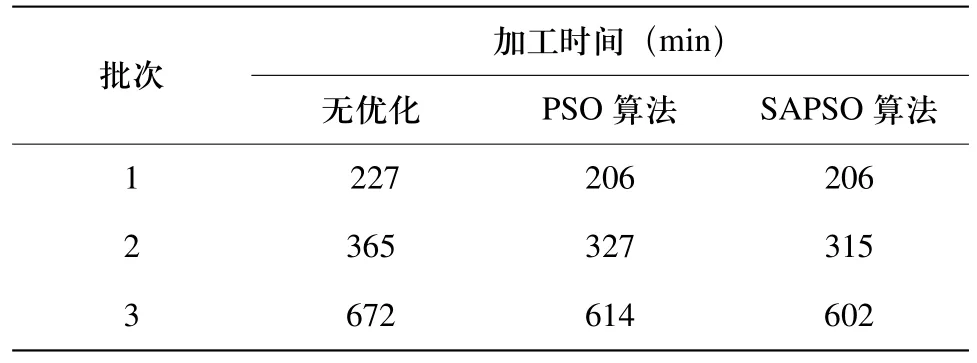
表1 不同批次工件的调度结果

4 结论

1）将模拟退火粒子群算法应用于钎焊炉生产调度。该混合算法在PSO算法中应用模拟退火机制，提高搜索过程中跳出局部极值的能力。

2）研究SAPSO算法在钎焊炉生产调度中的实际问题，给出粒子编码，目标函数及约束条件以及SAPSO具体实现步骤。

3）通过数值仿真实验验证论文中SAPSO算法的可行性和有效性，为工业热处理设置生产过程调度优化提供一种有效的方法。

[1] 管根笙. 热处理电炉的节能技术[J]. 热处理技术与装备,2007, (4): 58-60.

[2] 钟建安, 艾楠, 戴惠良, 周泽斌. 基于DCS的大型大型真空钎焊炉监控系统开发[J]. 机床与液压, 2009, 37 (4):109-111.

[3] 刘小华, 林杰, 邓可. 基于遗传粒子群混合的可重入生产调度优化[J]. 同济大学学报, 2011, 39 (5): 726-730.

[4] 宁树实, 王伟, 刘全利. 钢铁生产中的加热炉优化调度算法研究[J]. 控制与决策. 2006, 21. (10): 1138-1141.

[5] 谭园园, 宁健海, 刘士新. 加热炉优化调度模型及算法研究[J]. 控制理论与应用. 2011, 28: (11): 1149-1557.

[6] 唐海波, 叶春明. 仿生群智能算法在生产调度中的应用综述[J]. 工业工程, 2010, 13(3): 1- 5.

[7] Lotfi K G, Sherif A M,A shraf ON. A partic-le swarm-based genetic algorithm for schedul-ing in an agile environment[J].Computers&Industrial Engineering, 2008, 55 (3): 707.

[8] 王华秋, 曹长修. 基于模拟退火的并行粒子群优化研究[J].控制与决策, 2005, 20(5): 500-504.

[9] 焦巍, 刘光斌, 张艳红. 求解约束优化的模拟退火PSO算法[J]. 系统工程与电子技术, 2010, 32(7): 1532-1536.

[10] 魏东. NB式全自动氮气保护钎焊炉的结构及含氧量的控制[J]. 机械设计与制造, 2007, 2(3): 47-49.

[11] kennedy James, Eberhart Russell. Particle swarm optimization[C] //IEEE International Conference on Neural Networks, Perth, Austr-alia: 1995: 1942-1948.

[12] 李丽, 牛奔. 粒子群优化算法[M]. 北京: 冶金工业出版社, 2009: 88-89.

[13] 张建军, 彭来丽, 张利, 刘小平. 基于改进粒子群算法的多目铜卷加工生产调度研究[J]. 中国机械工程, 2011, 22(17):2061-2066.