过程工艺曲线综合相似模型及应用

李 俊，石 艳，周 敏，王维慧

（四川理工学院 机械工程学院，自贡 643000）

0 引言

由于经济或技术的限制（如工艺技术限制、缺乏适当的传感器），工业过程中一些重要的质量指标通常不便通过传感器在线实时测量。随着应用数学和计算机的发展，基于推断控制思想[1]，软测量（Soft sensor）技术应运而生，即根据易测过程辅助变量（即二次测量变量（Secondary Measurements）），对某些不可测主要变量（如质量指标）进行估计。20世纪90年代软测量被列为过程控制的几个主要发展方向之一[2]。目前，软测量的研究内容已从线性发展到非线性、从静态发展到动态、从无校正功能发展到有校正功能，成果瞩目[3]。模型是软测量技术的核心。然而，过程工业通常具有较复杂的机理和流程，产品质量受多个工艺参数和各种现场不确定性因素的复杂影响，无论是数据驱动建模还是机理建模，模型的泛化能力成为大多数软测量技术的主要障碍。在此情况下，控制好相关工艺参数并通过定期进行产品抽检和离线分析，以此来保证产品质量，这种方式不便于工艺改进和生产管理，而且耗时。

通常，产品质量是通过严格制定生产工艺并以此为依据进行实时控制来得到保证，生产过程主要工艺参数与拟定工艺之间的相似程度，既反映了工艺参数的控制质量，也反映了产品的质量。相似性是同类或异类对象的本质特征，相似性分析和定量描述在模式识别、数据挖掘、机器学习等领域已有着广泛的应用。然而，传统的相似度算

法由于其研究应用目的不同，对于过程工业复杂过程曲线之间的相似度分析，有着一定的局限性。本文根据复杂过程工艺曲线与产品质量之间的关系及特点，借助于过程工艺曲线之间的对比分析，建立过程工艺曲线之间的综合相似度模型，并在磁瓦烧结过程温度曲线相似分析中进行了应用。

1 相似度概念

曲线之间的相似性测度一般可以通过某种距离测度数值指数来表示，如Minkowski距离、欧氏距离（Minkowski距离的特例）、Fréchet 距离和Hausdorff距离。在模式识别及相关领域中，最典型的是Hausdorff距离和Fréchet距离。

定义1[4,5]：设有离散点集P,Q:[0,1]→R2表示的曲线，表示欧氏范数，则Hausdorff 距离和Fréchet距离分别定义如下：

1）设δH(P,Q)表示P和Q之间的Hausdorff 距离，则：

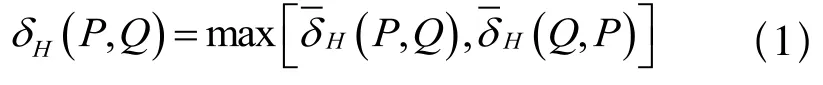
其中，

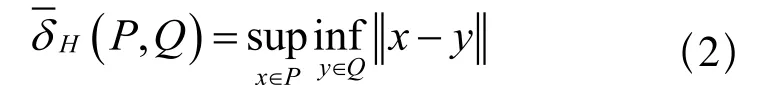
2）以 δF(P,Q)表示P和Q之间的Fréchet距离，则：

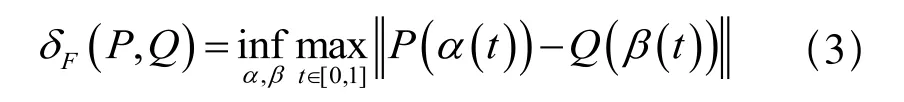
其中，α,β:[0,1]→ [0,1]是任意非降函数，α(0)=β(0)=0，α(1)=β(1)=1。定义2[6]：给定两曲线的函数ΘA(s),ΘB(s)，基于函数空间Lp度量定义曲线间的相似度：

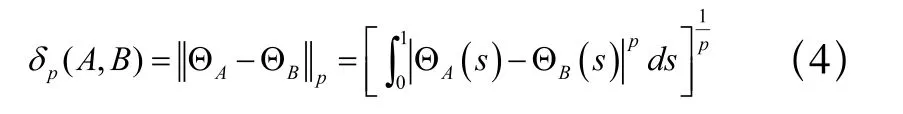
上述相似度定义以曲线的点集或特征集为数据集，基于Minkowski距离测度来描述曲线间值的差异，并根据两个数据集之间的最大距离值是否小于给定阈值参数ε进行相应的决策判断或分类。复杂生产过程的产品质量往往受到不同工艺参数不同程度的影响，且工艺历程不同阶段的影响程度不同，传统相似度没有考虑这些特点；同时，传统相似度对测量过程中的异常点和增益比较敏感，缺乏对曲线形态相似的表征。

2 工艺曲线综合相似度模型

曲线间的相似包括距离相似和形态相似。理论分析和实验结果表明[7]，任何一种方式均不能全面的反映两个曲线或向量之间的相似或差异，两种测度的综合可以更合理、更准确地描述曲线之间的相似性。同时，复杂生产过程往往受到不同工艺参数不同程度的影响，工艺历程不同阶段的影响程度不同，工业现场测量不可避免地存在异常点。然而，传统的相似度大多以经典距离度量反映两条曲线之间值的差异或相似，不足以表征这种差异的分布信息，也没有反映出复杂过程生产过程的特点，而这些是复杂过程曲线相似性分析需要考虑的基本因素。

数学上，曲线形态变化可通过切线的变化来表征。对于二维工艺曲线，在时间坐标（横坐标）确定的情况下，可以离散数据集的差分来表征曲线的形态变化，如果将横坐标轴对应的采样周期长度作为单位量，差分量的反正切值可近似为曲线各点与横坐标轴的夹角（范围为[-π/2,π/2]），而反正切函数在[-π/2,π/2]上是单调函数，且对异常值不敏感。同时，熵信息表征反映的是数据分布的随机特性，数据分布越不均匀其熵值越小，反之越大。因此，在复杂过程曲线相似性分析中引入熵，既可以表征出曲线某种属性的相似性，又可以反映出这种相似沿曲线的分布信息。

假设一个生产过程，有M个对产品质量或性能有重要影响的工艺参数，不同参数对产品质量性能的不同影响用向示；不同工艺参数对应的拟定工艺曲线和实时工艺曲线分别为Pi和 Qi(i=1,2,…,M)，对应的离散点集 分 别 为 {Pi(t1),Pi(t2),…,Pi(tTi),} 和 {Qi(t1),Qi(t2),…,Qi(tTi),} （Ti为第i个工艺参数的采集点数或生产周期）；由于工艺历程不同阶段对产品质量的影响程度可能不同，将一个生产周期内的工艺曲线分成N个不同阶段，对产品质量性能的影响用向量

首先，构造差分向量：

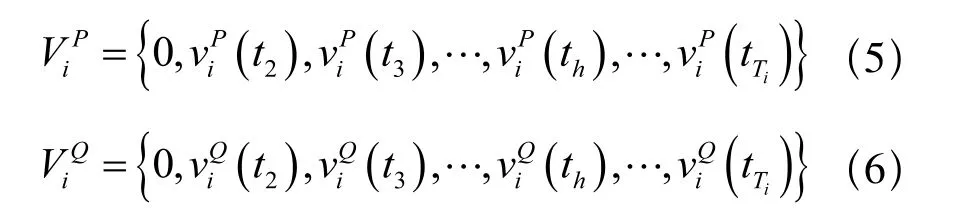
其中，

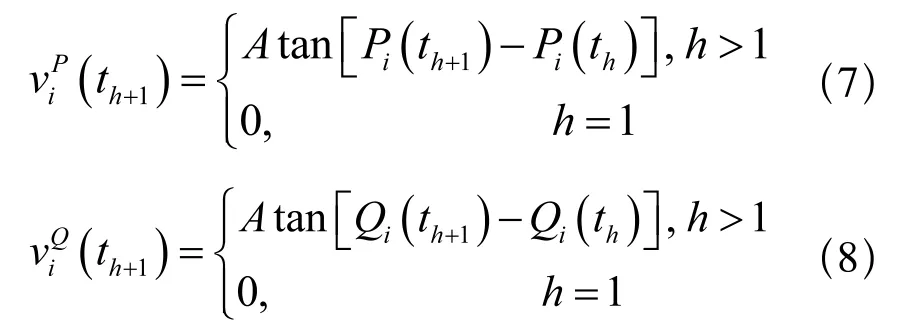
根据曲线间的角度差定义形态相似度，

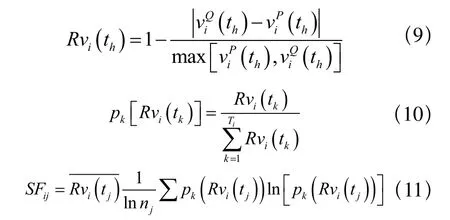
其中，SFij即为曲线之间的形态相似程度，nj为j段的数据点数。

同时，根据曼哈顿距离，曲线间的距离相似可表示为：

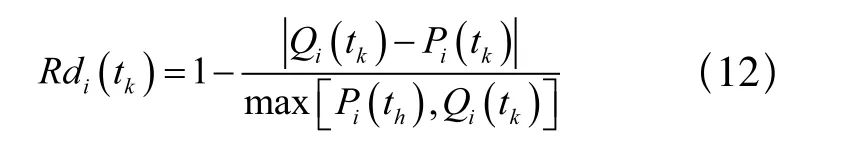
Rdi(tk)反映了工艺参数的实时值相对于设定值（即拟定工艺值）的波动情况，也是控制误差的反映，Rdi(tk)越大则表示偏差越小，控制效果越好，对产品质量的影响越小。

根据信息熵定义曲线距离相似度为：

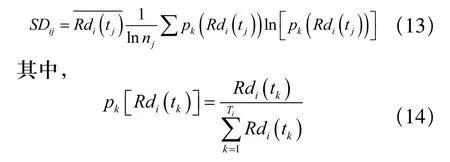
由式（11）和式（13）定义过程曲线综合相似度为：

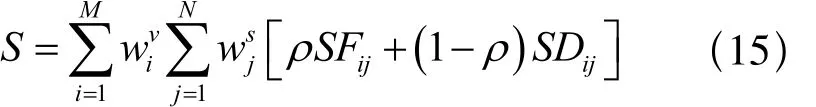
其中，ρ为综合考虑数据变化特征后所确定的形态相似度对综合相似度的影响系数。

3 磁瓦烧结过程工艺曲线相似性分析

烧结是磁瓦生产的关键工序，烧结工艺及其检测控制水平直接影响到固相反应程度及最终的材料组成、密度、晶粒大小、机械强度、外观尺寸等，对磁瓦的性能、机械强度和物理特征起着决定性的作用，烧结温度是最的关键控制参数，包括升温速率、最高温度、保温时间和降温速度[8,9]。烧结炉炉体长，烧结过程长达10多个小时，烧结过程复杂，不确定性因素多，为了对烧结坯件的质量和性能进行控制，并方便工艺改进和生产管理，下面应用曲线相似度模型对烧结过程温度控制性能进行评价，以此作为磁瓦烧结控制和质量评价的参考。图1是磁瓦烧结拟定工艺曲线与仿真曲线的相似性分析。

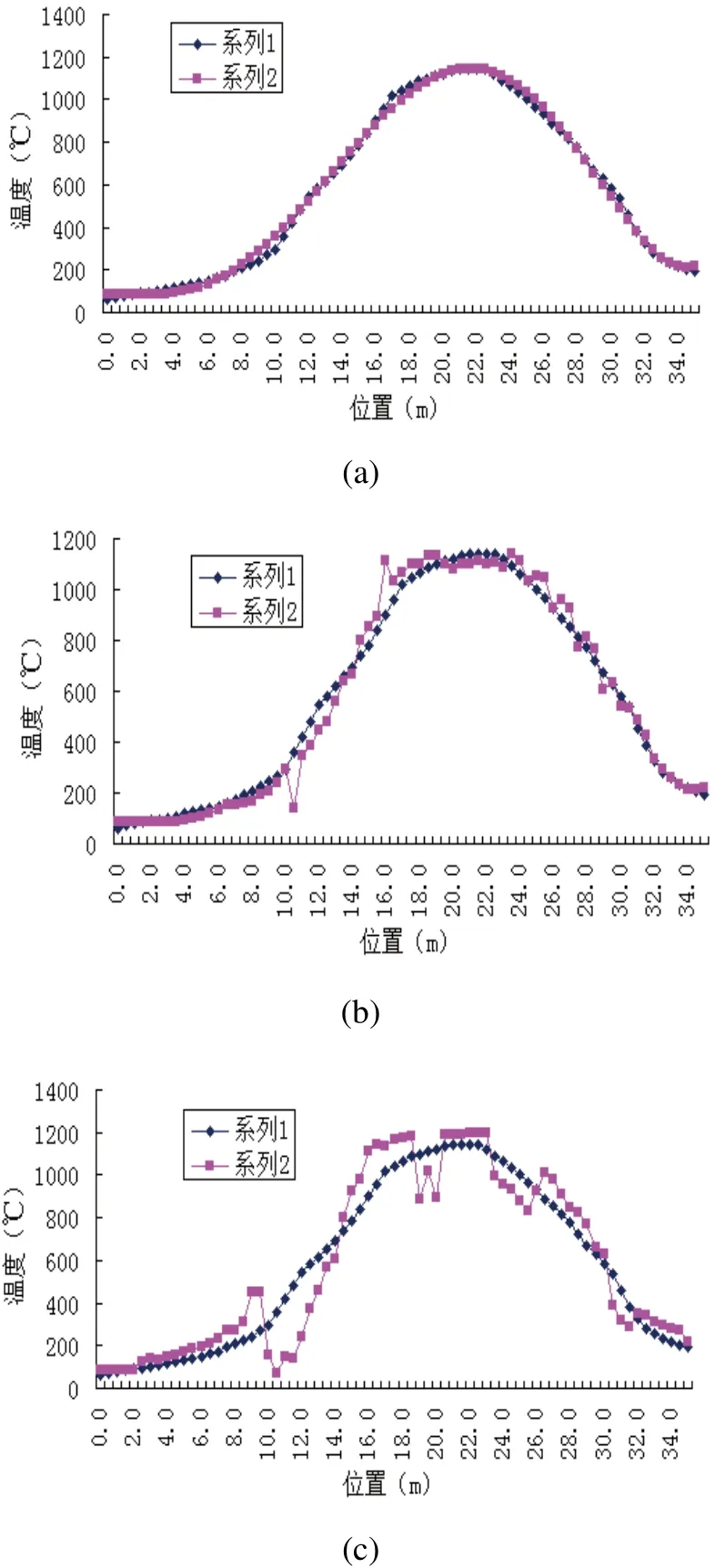
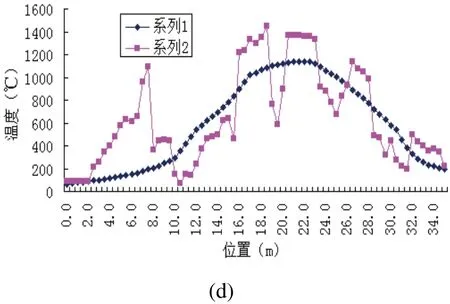
图1 磁瓦烧结温度曲线对比

根据磁瓦烧结工艺，将烧结温度曲线分成五个阶段，ρ=0.3，Ws={0.15,0.25,0.2,0.25,0.15}，在实际生产过程中，针对具体情况（产品性能和原材料等），向量Ws和ρ的确定也不同。据综合相似度算法，图1的计算结果如表1所示。

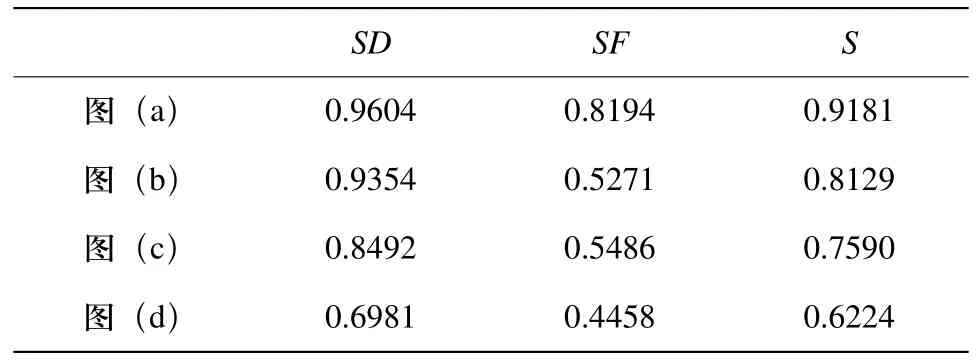
表1 相似性计算结果

由表1可知，从图1（a）～（d）距离相似性减小，说明过程曲线间的距离波动越大，其距离相似性越差；图1（a）的形态相似性较图（b）大，说明在距离差相差不大的情况下，曲线变化平缓时具有较高的相似度，过程曲线变化越频繁，曲线的形态波动越大，形态相似性降低。上述结果表明，过程曲线相似度能够反映实际过程曲线的相似性。

4 结束语

过程工艺曲线的相似性分析对于过程工艺控制性能的在线分析和工艺改进具有重要意义。传统相似度以距离测度为基础，没有考虑曲线间的差异分布情况和复杂生产过程的特点，且缺乏对曲线形态相似的表征，不适于过程工艺曲线的相似性分析。本文以信息熵为基础，借助于差分向量方向角的变化来表征曲线形态变化，以传统距离测度表征曲线间的距离相似，并考虑复杂生产过程受不同工艺参数不同程度的影响，以及工艺历程不同阶段的不同影响，建立适合于复杂生产的过程工艺曲线相似性综合分析模型。应用表明，研究模型能够用于复杂过程曲线的相似度分析。

[1] Brosilow C. Inferential Control of Process[J]. AIChE. J.,1978, 24(3): 485-509.

[2] Macvoy T J. Contemplative stance for chemical process control [J]. Automatic, 1992, 28(2): 441-442.

[3] Ming T Tham, Gary A Montague, et al. Soft-sensor for process estimation and inferential control [J].J. proc. Cont,1991, 1(1): 3-14.

[4] H. Alt, C. Knauer, C. Wenk. Comparison of distance measures for planar curves. Algorithmica, 38(1): 45–58,2004.

[5] Eiter T.and Mannila H. Computing Discrete Fréchet Distance[R]. Austria:Technical Report CD-TR94/64,Information Systems Department, Technical University of Vienna, 1994.

[6] Esther M., Arkin L., Panl Chew, et al. An Efficiently Computable Metric for Comparing Polygonal Shapes[J]. IEEE: Trans. On Pattern Analysis and Machine Intelligence, 1991, 3(13): 209-216.

[7] WEN Bing-gong, FENG Wu-fa, LIU Wei, MA Yiwei. Matching and Classification Based on the Whole Comparability Measure of Spectral Curve [J]. Journal of Geomatics Science and Technology, 2009, 26(2): 128-131.

[8] 陈家才, 甘国友, 严继康, 等. 高性能烧结永磁铁氧体生产工艺的探讨[J]. 云南冶金, 2006, 35(4): 36-41.

[9] 吴新元. 铁氧体磁瓦机械强度影响因素分析[J]. 磁性材料及器件, 2007, 38(6): 61-62.