航天器随机振动和噪声试验条件设计方法

张玉梅，韩增尧，邹元杰

（北京空间飞行器总体设计部，北京 100094）

0 引言

航天器在全寿命期间，要经历运输、装卸、起吊、发射、飞行、分离、着陆、返回等过程中诱导产生的包括振动、噪声、冲击和加速度在内的动力学环境，而这些环境是诱发航天器故障的重要原因。美国戈达德空间中心曾对在发射第一天就出现故障的57颗卫星进行过统计，其中振动及噪声环境所引起的失效约占1/3[1]。由此可见，航天器在发射前通过适当的动力学环境模拟试验以提前暴露潜在故障，对于确保其任务成功十分重要。

早在1965年，NASA就提出了航天器动力学环境模拟试验的原则：1）若试验件在试验中工作良好，则它在工作环境中也能正常工作；2）如果试验件在试验中不能正常工作，那么它在工作环境中也不能正常工作。第一个原则意味着试验条件应当至少跟工作环境同等严酷。第二个原则意味着试验条件不能无道理地增加其严酷性[2]。在工程实现上，第一个要求比较容易实现，而第二个要求则难以把握，这就是很多航天器过试验的原因。

如何合理地制定试验条件，既要能充分暴露缺陷又要避免过试验，一直是模拟试验研究的课题。航天器发射段动力学环境的模拟试验包括静力试验、正弦振动试验（定频和扫频）、随机振动试验以及噪声试验。其中，随机振动和噪声的试验条件较为复杂，包括试验目的、试验对象的结构、试验量级、试验时间、试验容差等，而试验量级及试验时间又是最关键的试验条件[3]。因此，本文将对相关试验条件的设计方法予以重点介绍。

1 试验量级的设计方法

试验量级的设计方法主要有极限包络法、正态容差限法、非参数容差限法、经验容差限法和正态预示极限值法，其中较为常用的是极限包络法和正态容差限法。

1.1 极限包络法

极限包络法是我国目前采用的方法，即用最大谱来描述随机振动与噪声环境。最大谱就是每个频率上谱密度的最大值，但在实际计算中往往不会逐一计算每个频率，而是以一定的带宽来划分。以噪声载荷为例[4]，其计算过程为：用连续均值来计算每一个带宽（通常为1/3倍频程）的非平稳振动事件的声压级 （SPL）；确定每个带宽内的SPL最大值，与最大值的发生时间无关；将每一个带宽内的最大值连接起来得到最大 SPL谱值。为了简化，经常用一系列直线段（NASA HDBK7005规定为：直线数量通常不大于7条，斜率为 0、±3 dB/oct或±6 dB/oct）使之光滑。

极限包络法的主要优点是容易实施，但也有以下不足：振动与噪声都是随机过程，因该方法没有采用概率来描述随机过程，使得其不确定性无法量化；采用不同的带宽会产生一定的差异；试验量级的制定带有一定的主观性，即两个有经验的工程师用相同的数据可能得到完全不同的光滑的极限。

1.2 正态容差限法

正态容差限法只适用于正态分布随机变量，但大量的试验证据表明飞行器声振响应近似满足对数正态分布。因此，通过简单的对数变换

就可以估算其正态容差极限，式中x为结构响应。

设y的单边（上半部分）正态容差极限表示为NTLx(n,β,γ)，式中：β为百分比；γ为置信度；n为试验样本数。其计算分为3种情况：

1）试验样本数n≥3，并且数据来自的试验次数m≥3；

2）试验样本数n≥3，但是试验次数m＜3；

3）试验样本数n＜3。

相应地，NTLx(n,β,γ)值对应的也有3种情况，见表1，其中：Zα为正态百分位，在此Z0.05=1.645；σflt-to-flt上限为 3 dB；σspatial上限为 6 dB；Kn,β,γ为正态容差因子；β为95%；γ为50%。

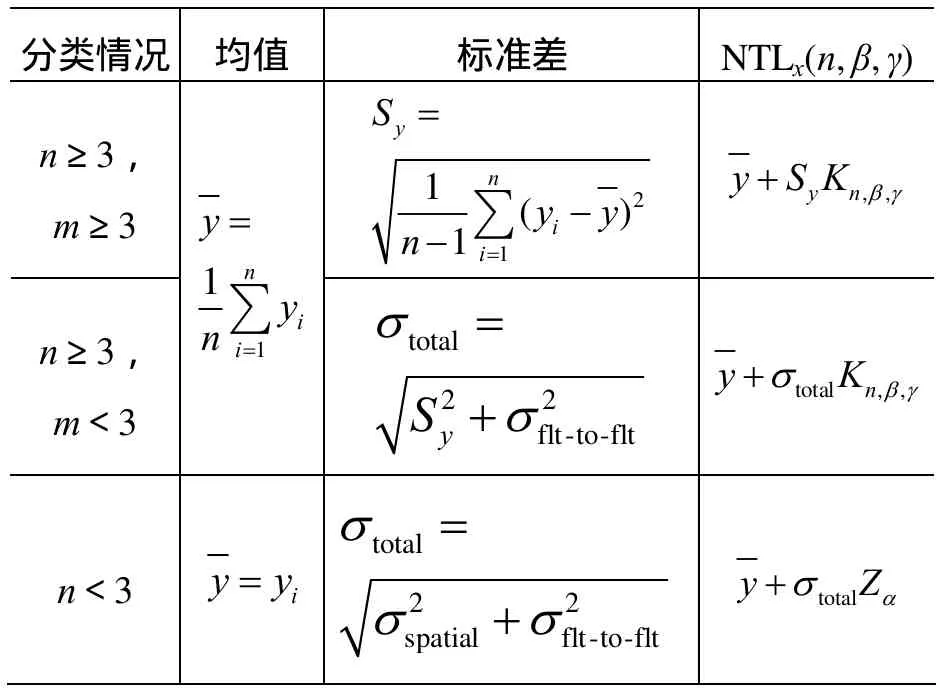
表 1 3 种情况下 NTLx(n, β, γ)值的确定Table 1 NTLx(n, β, γ) in three cases

在表1中常见的是第一种情况，其中Kn,β,γ为[5]

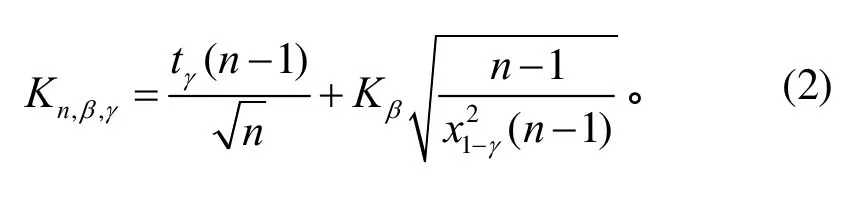
国军标中采用的也是这种方法[6]。需要注意的是，该正态容差因子计算数值过大，容易造成过试验。

正态容差因子的另一种比较准确的计算方法[7]是

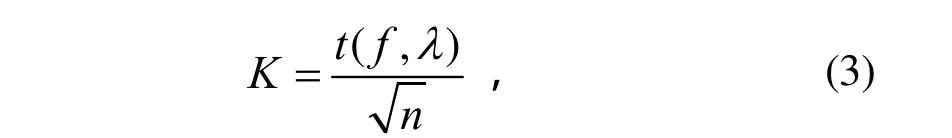
采用β= 0.95 和γ= 0.50 计算的正态容差极限通常被称为有50%置信度的95%正态容差极限，即 P95/50极限。50%置信度是指：在美国空军空间系统部（AFSSD）历史上仅有一个数据可用的情况下，其大于和小于真实值的概率是相等的。沿袭至今，即使有足够的测量数据允许选用更高的置信度，仍然采用P95/50[8]。

正态容差限法与极限包络法相比有如下主要优点：

1）正态容差限有一个精确的统计分布；2）n取任何值，都可以计算正态容差限；

3）尽管预示谱的带宽对正态容差极限有一些影响，但正态容差限法不如极限包络法对带宽敏感。

正态容差限法的缺点是结构响应谱值的空间分布对对数正态分布的假设敏感，尤其是当β和γ的值较大时。

1.3 余量的制定

对于不同研究机构甚至不同项目，试验余量都可能相差很大，但是最为常用的余量如表2所示，表中最大期望环境（MEE）用95/50的标准公差极限来定义。

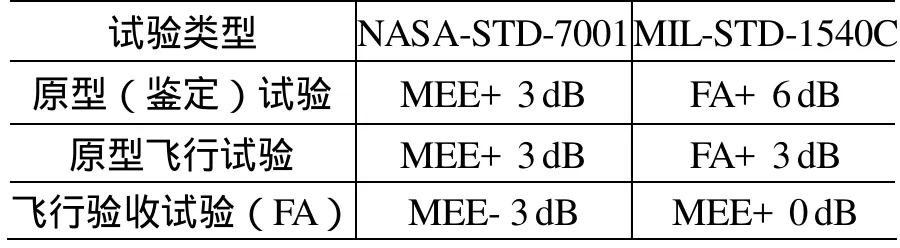
表 2 高频随机振动和噪声试验的试验余量等级Table 2 Specifications of high frequency random vibration and acoustic test margins

2 试验时间的设计方法

如果用整个动力学环境时间作为试验时间，那么试验显然是过于严酷了。但如果试验时间只取最大振动水平的时间，又会造成欠试验。因此需要精确计算试验时间，以获得与实际振动环境相同的损伤。计算试验时间的方法主要是根据以下3种失效模型。

2.1 逆幂律模型

逆幂律模型是最为典型的一种加速模型，广泛应用于加速寿命试验。对于可靠性高、寿命长的产品，不可能用实际的工作时间来评估其可靠性，因此产生了加速寿命试验，即采取载荷大于实际载荷、而时间小于实际时间的方法来模拟实际工况。其核心即加速模型，是产品寿命与载荷之间的数学关系[9]。

20世纪，有学者开始研究电应力对产品（主要是电子设备）寿命的影响，并构造了逆幂律模型[10]为

式中：b、c是与硬件类型有关的常数；TF为疲劳寿命；σX是随机载荷的均方根值。

NASA将其推广应用于动力学环境下的机械设备。对于随机振动，不同均方根值的激励若要产生相同的损伤，则需要满足

式中：T1、T2表示两个随机振动过程的持续时间；σ1、σ2表示两个随机振动过程的均方根值。

运用该方法的主要问题是选取合适的参数b。对于不同的产品，b的取值是不同的。针对小型导弹，美国在大量的、详尽的试验后得出：对于电子器件，b= 4是合适的。对于航天器硬件，在用平稳随机振动模拟非平稳随机振动时，美军标[11]中仍然采用b= 4。这种方法最为常用也最为简单，但是有时过于保守。

2.2 疲劳损伤

疲劳损伤是工程领域常见的失效方式，主要有以下两种模型：

1）S-N曲线模型

结构疲劳是较为复杂的问题。然而，如果载荷是产生一定应力水平后的重复作用，高度简化后，可认为是积累损伤产生裂纹，裂纹逐渐扩展直至断裂。一定的应力水平是指材料的疲劳阈值，即应力达到这个水平，疲劳损伤才会产生并积累。通常用S-N曲线来研究疲劳问题。进一步简化，不考虑疲劳阈值，并且取对数可得

式中：N为载荷循环次数；S为峰值应力；b、c均为材料常数。对于铝合金，b通常取值6～9；美军标[12]中，随机振动时b取8。1970年的NASA报告[13]对S-N曲线模型进行了更加详细的论述，其中考虑了疲劳阈值的问题。

2）裂纹扩展率模型

用裂纹扩展率模型研究疲劳问题是断裂力学的基本原理。一旦裂纹起始，利用该模型就可以精确地预示疲劳寿命。但是裂纹起始状态的正确描述比较困难，这也是该模型产生误差的最大原因。因为裂纹起始状态与材料界面的光滑度等因素有关，难以精确预计，而裂纹扩展率模型计算公式又依赖于裂纹初始长度，这使得不同应力环境下的损伤难以计算，所以这种方法 NASA并未使用，本文也就不详加叙述。

2.3 首次穿越模型

1959年，J. J. Coleman首次提出的首次穿越模型[14]是异于疲劳损伤积累的一种脆性破坏形式。文献[14]中假定结构在随机振动下的响应呈正态分布且结构的应力超过许用值就会发生破坏，提出了计算失效时间的Possion模型。

对于平稳随机载荷，超过许用响应值的概率随着时间的增加而增加。如图1所示。

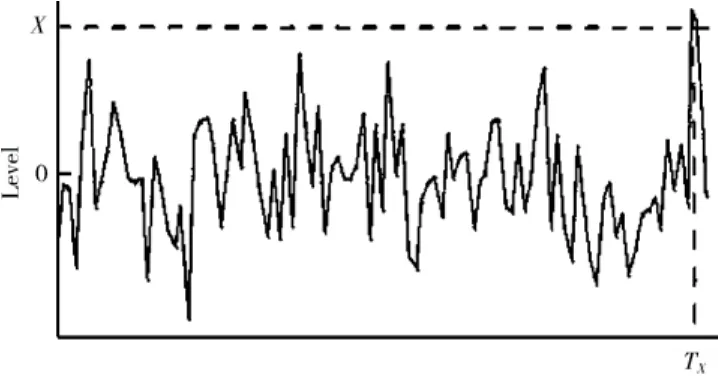
图1 随机载荷穿越极值Fig. 1 Exceedance of a critical level under a random load

设x(t)是关注的响应参数（如加速度、应力、位移等），且x(t)呈零均值高斯分布，其功率谱密度为GXX(f)，标准偏差为SX，那么在时间TX内响应超越许用值X的概率为

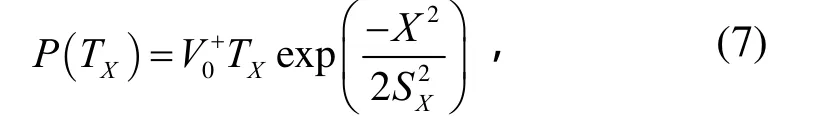
将式(7)简单变换即可计算失效时间为

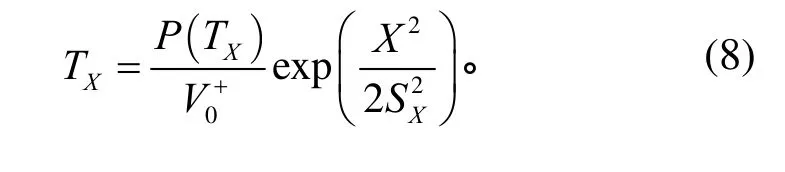
进一步假设响应x(t)取决于第一阶模态响应，则≈fn，fn为结构第一阶模态频率。所以式(8)可写为

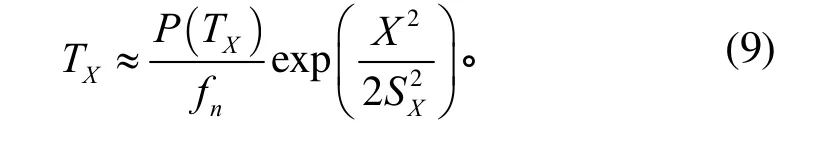
因此，不同的均方根值下的随机激励可以具有相同的失效时间，其等效关系式为

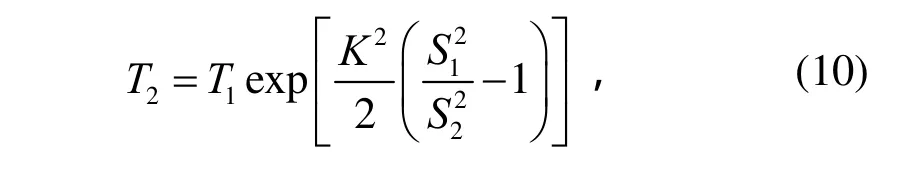
用上述首次穿越模型来预计失效时间，有两个主要问题：

1）引起失效的参数值X不明确。传统的关注参数为加速度，20世纪末有学者提出应该关注应力。

2）模型中假设结构响应呈正态分布，但很多因素都会导致响应不呈正态分布，如响应具有周期性组成部分或者结构呈现非线性。

近50年来，首次穿越模型得到了长足的发展。非高斯首次穿越问题已得到解决[15]，但是关于参数值X的取值问题仍然缺乏相关研究。

由于以上模型都存在缺陷，所以为了保证高可靠性，当计算出等效试验时间以后，还需要乘以系数。原型飞行试验的系数如表3，原型试验如表4。需要强调的是，NASA-STD-7001中规定了试验的最短时间，在实际应用中，试验时间不得低于规定的最短时间[16]，见表5。

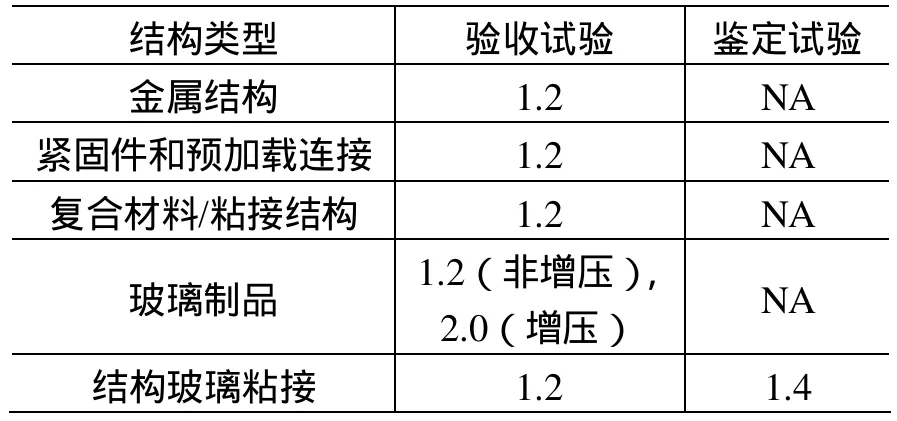
表3 原型飞行试验时间系数Table 3 Flight test duration factor for prototype

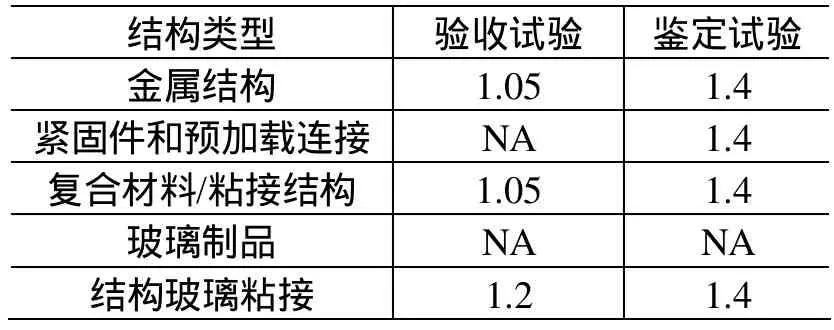
表4 原型试验时间系数Table 4 Flight test duration factor for prototype

表5 最短试验时间Table 5 Minimum test duration

3 结束语

随机振动试验和噪声试验是航天器动力学环境模拟试验的重要内容。合理制定试验条件是进行有效试验的先决条件。国内由于缺乏充分的数据支撑和前面的设计理论指导，在确定试验条件的某些环节仍处于较为保守的状态。因此该研究领域具有很高的工程应用价值。建议进一步开展如下研究工作：

1）试验量级的设计本质上是对随机过程的描述。正态容差限法给出了具体的概率，这相对于极限包络法是一大进步。因为对于随机过程，极大值理论上可以无限大。但是与非参数容差限法、经验容差限法和正态预示极限值法这几种方法比较，正态容差法的优势并不明显。关于这几种方法的比较工作需要进一步研究。但无论采用哪种方法，充足的飞行数据都是必须的。因此应加强飞行遥测数据的收集整理和分析研究工作。

2）试验时间的设计方法关系到失效机理。对于静载下的失效机理是较为明确的，然而在航天器发射段复杂力学环境下的失效机理并不清晰，现有的各种失效模型均有一定不足，在实际应用中，计算分析得到的试验时间常常会低于最短试验时间。因此研究航天器发射段失效机理进而修正失效模型，也是下一步工作应重点考虑的问题。

（

）

[1]柯受全. 卫星环境工程和模拟试验[M]. 北京: 宇航出版社, 1993: 11

[2]Klein G H, Piersol A G. The development of vibration test specifications for spacecraft application, NASA CR-234[R], 1965-05

[3]NASA-HDBK-7005 Dynamic environmental criteria[G],2001-03

[4]Himelblau H, Piersol A G, Wise J H, et al. Handbook for dynamic data acquisition and analysis[G]. Inst Envir Sc Tech. MtProspect, IL, 1994

[5]徐明. 随机振动环境测量数据归纳的统计容差法[C]∥中国航空学会环境工程学术年会, 2001

[6]GJB/Z 126—1999 振动、冲击环境测量数据归纳方法[S], 1999-08

[7]袁宏杰, 罗敏, 姜同敏. 随机振动环境测量数据归纳方法研究[J]. 航空学报, 2007, 28(1): 115-117 Yuan Hongjie, Luo Min, Jiang Tongmin. Study on inductive method for environmental measured data of random vibration[J]. Acta Aeronautica et Astronautica Sincia, 2007, 28(1): 115-117

[8]李春丽, 邓克文. 关于航天器最高预示环境的探讨[J].导弹与航天运载技术, 2008(5): 35-38

Li Chunli, Deng Kewen. Discussion on the maximum expected environment of spacecraft[J]. Missiles and Space Vechicles, 2008(5): 35-38

[9]张仕念, 赵韶平. 加速寿命试验的数学模型[C]∥中国电子学会可靠性分会, 2006

[10]李晓阳, 姜同敏. 加速寿命试验中多应力加速模型综述[J]. 系统工程与电子技术, 2007, 29(5): 828-831 Li Xiaoyang, Jiang Tongmin. Review of multiple-stress models in accelerated life testing[J]. Systems Engineering and Electronics, 2007, 29(5): 828-831

[11]MIL-STD-1540C Test requirements for booster, upperstage, and space vehicles[S], 1994

[12]MIL-STD-810F Department of defense test method standard for environmental engineering considerations and laboratory tests[S], 2000-01

[13]Himelblau H, Fuller C M, Scharton T D. Assessment of space vehicle aeroacoustic-vibration prediction, design,and testing, NASA CR-1596[R], 1970-07

[14]Coleman J J. Reliability of aircraft structures in resisting chance failure[J]. Operations Research, 1959, 7(5):639-645

[15]郑春林, 寇新建. 非高斯结构首次屈服的概率模型[J].福州大学学报: 自然科学版, 2005, 33(z1): 106-109

Zheng Chunlin, Kou Xinjian. Probabilistic model for the first yield of non-Gaussian structures[J]. Journal of Fuzhou University: Natural Science, 2005, 33(z1): 106-109

[16]NASA-STD-7001 Payload vibroacoustic test criteria[S],1996-06