转子系统临界转速计算及不平衡响应分析

瓮 雷，杨自春，曹跃云

( 海军工程大学 船舶与动力学院，武汉 430033)

转子是舰船汽轮机的重要部分，由于转子的工作环境非常恶劣，长期处于高温介质中并且高速旋转。它承受着由转子本身和叶片质量的离心力引起的应力、温度分布不均匀引起的热应力、传递作用在叶片上的气流力产生的扭矩、工质的压力和自身重量产生的弯矩等。任何设计、制造、运行等方面的失误，都可能会造成转子部件的断裂而引起重大事故［1］。

振动是旋转机械转子发生故障的主要问题之一，一般不允许转子在临界转速或接近临界转速附近运转，因为在临界转速附近运转会产生很大的振动应力，轻则机组内部动静部件部分碰撞摩擦，重则造成汽封油封机构的损坏，轴承损伤甚至转子弯曲，整个机组损坏［2］。振动产生的原因比较复杂，但是大多数与转子质量不平衡和临界转速设计不合理有关［3］。舰船汽轮机转子系统动态特性的分析是转子动力学研究中的一个重要课题，国内外学者对转子的临界转速及其不平衡响应做了大量的研究分析［2-7］。研究舰船汽轮机转子的振动特性，对其进行振动噪声改进，降低舰船辐射噪声，对舰船航行的安全性、可靠性具有重要的意义［8］。

目前，关于汽轮机转子系统振动特性分析方法主要有解析法、传递矩阵法、有限元法、不平衡响应法及模态合成法。解析法和模态合成法主要针对简单转子求解理论解，而有限元法及传递矩阵法主要应用于复杂的多盘或多轴承系统。陀螺效应一直是有限元计算临界转速的关键问题，与传递矩阵法相比能够充分模拟转子的振动特性，且具有较好的计算精度。文献［6］基于ANSYS 软件对转子系统分别用传递矩阵法、线型模型直接写入矩阵方法、简谐轴对称模型子程序法和三维实体模型子程序法进行计算，计算结果表明与传递矩阵法相比有限元法计算速度快，具有较好的计算精度。因此，将采用ANSYS 有限元转子系统线型模型，对转子轴承系统的临界转速及不平衡响应分析研究。

1 转子动力学分析理论基础

有限单元法的基本思想是将连续的求解区域离散为一组有限个，且按一定方式相互连接在一起的单元的组合体，由于单元能按不同的连接方式进行组合，且单元本身又可以有不同形状，因此可以对复杂的模型进行求解。对于一个实际连续的转子系统，经离散化后就变成一个多自由度系统。根据弹性力学有限单元理论，对于一个N 自由度线性弹性系统，其通用基本动力学运动方程［9］:

式(1) 中，[M] 、[C] 和[K] 分别表示系统整体的质量矩阵、阻尼矩阵和刚度矩阵分别表示加速度向量、速度向量和位移响应向量; {F} 为动激励载荷向量。

在转子动力学中，方程(1) 要增加陀螺效应和旋转阻尼，其动力学方程如下:

式(2) 适合用于在一个固定的参考框架计算转子运动，[G] 、[B] 分别是陀螺矩阵和旋转阻尼矩阵。陀螺矩阵[G] 取决于转速，并且对转子动力学计算做主要贡献，这个矩阵对于转子动力学计算分析是必不可少的。旋转阻尼矩阵[B] 也取决于转速，且明显地修改结构刚度，并且能够使结构产生不平稳的运动。

2 转子系统的有限元模型

转子作为旋转机械的核心部件，本身零件数量多，属于大型装配体，在高温、高压、高流量的环境中运行，所涉及的相关理论复杂，如流体力学、工程热力学、机械学、固体力学、材料力学等等。这里只考虑影响转子动力学性能的主要因素，对转子系统进行简化，这样有利于降低问题的复杂程度，且可以节省分析的时间，提高分析效率。文献［10］利用转子零件之间的关系，依据质心不变、质量不变等原则对转子本体进行简化，将转轴、叶轮、叶片进行简化为圆盘、转轴和支承等典型部件。

2.1 模型的几何参数

运用ANSYS 软件对典型的转子轴承系统进行建模，该转子系统长度为2.35 m，由两个转盘、四根转轴、两个轴承组成，给出简化后的转子轴承系统力学简图如图1 所示，模型的几何参数如表1 所示。

图1 转子轴承系统的力学简图

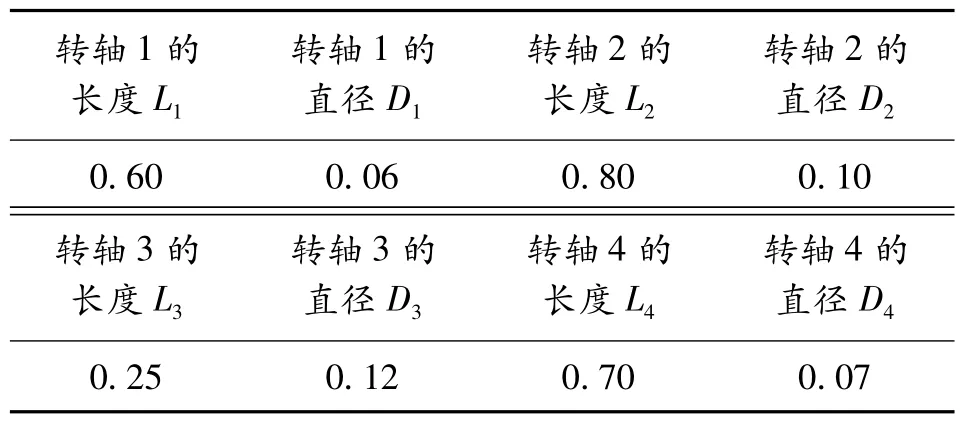
表1 转子系统的几何参数

2.2 有限元单元选择及材料常数

转子的有限元模型采用MASS21 模拟刚性转盘，MASS21为点单元，具有x，y，z 位移与旋转的6 个自由度，不同质量或转动惯量可分别定义于每个坐标方向，假定转盘质量均匀，可以忽略其对转子系统不平衡响应产生的影响。使用COMBIN214 模拟轴承，COMBIN214 是专门用来模拟轴承力学性质的单元，可以考虑拉压，但不能考虑弯曲和扭转。使用BEAM188 模拟转轴，在Beam Tool 面板中定义截面形状为圆形。BEAM188 单元是三维线性有限应力梁单元，适用于分析短粗梁结构，该单元基于Timoshenko 梁理论，包括剪应变且具有分析屈曲、侧移和扭转的能力。转轴1 的质量m1=50 kg ，极转动惯量JP1=4 kg·m2，直径转动惯量JD1=2 kg·m2，转盘2 的质量m2=20kg，极转动惯量JP2=2 kg·m2，直径转动惯量JD2=1 kg·m2。轴承的平面为YZ 平面，通过设置关键字来实现。所有轴承材料的弹性模量相同，只考虑轴承两个方向的刚度，忽略轴承阻尼。转子轴承系统的材料常数如表2 所示。

表2 转子轴承系统材料常数

采用先建立节点，然后生成单元的有限元建模方法，整个转子系统有限元模型共包含121 个节点，120 个梁单元，2个轴承单元。建立的转子系统的有限元计算模型如图2。

图2 转子轴承系统有限元计算模型

3 转子系统有限元计算分析

3.1 临界转速求解

旋转机械转子临界转速的确定是转子动力学的一个基本课题，合理设计转子系统的临界转速，对机组的安全可靠运行的重要前提。本转子轴承系统不考虑剪切和扭矩影响，因此只需对有限元模型X 方向平动位移和转动位移进行约束，定义绕转轴的平动位移UX 和转动位移ROTX。且考虑陀螺效应的影响，设置陀螺效应Coriolis 为ON。转子轴承系统加载约束条件如图3 所示。设置分析类型为模态分析Modal，采用QR Damped 模态提取方法，在No.of nodes to extract和NMODE No.of modes to expand 选项中设置模态提取阶为20。

图3 转子轴承系统载荷加载图

为了获取转子轴承系统的临界转速，需要通过ANSYS有限元分析获取CAMPBELL 图，绘制CAMPBELL 图需要求出多个自转频率值对应的进动频率，因此设置考察转子的转速分别为0，2 000，5 000，8 000，9 000，10 000，110 000，单位是r/min。进行多次模态求解后，利用命令PRCAMP，，1，RPM/PLCAMP，，1，RPM 获得转子轴承系图的坎贝尔图如图4 所示，图4 中FW 为正向涡动，BW 为反向涡动。

在ANSYS 中，激励直线与各阶频率曲线的交点对应的转速即临界转速，如表3 所示。

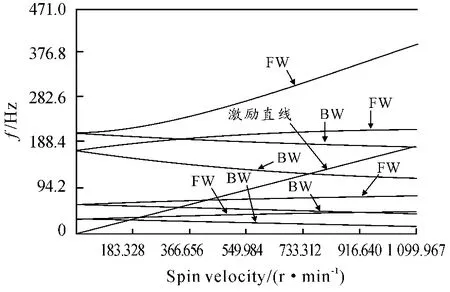
图4 坎贝尔图

表3 与各阶频率曲线的交点转速

在计算转子临界转速时，通常只考虑同步正向涡动时的振动频率，这是因为在实际转子运行时，由于不平衡激励力的存在，转子将做同步正向涡动，通常说的临界转速，一般是指同步正向涡动的临界转速［8］。由坎贝尔图图4 可以看出第1、3、5 阶频率为反进动的频率，第2、4 阶为正进动的频率。因此，转子轴承系统的存在两阶临界转速为1 920 r/min、3 624 r/min。图5 ～12 是利用ANSYS 谐响应分析转子系统在不平衡力下的不平衡响应，由图5 -12 可以看出转子轴承系统在频率31 Hz(1 860 r/min) 、60 Hz(3 600 r/min) 处的振动幅值最大发生共振，由于转子在其临界转速附近的振动幅值最大，从而验证了求解转子系统临界转速的正确性。

3.2 不平衡响应分析

为模拟转子轴承系统实际工作情况，研究转子圆盘偏心质量所引起的离心力对转子系统的影响，为进一步舰船汽轮机转子的优化设计分析提供理论依据。由理论力学可知，假如在某一圆盘上的偏心质量，则其产生的离心力:

式(3) 中，F 为离心力，m 为偏心质量，r 为偏心半径，ω 为转子的旋转速度。偏心力在转子中心上两个坐标方向的投影:

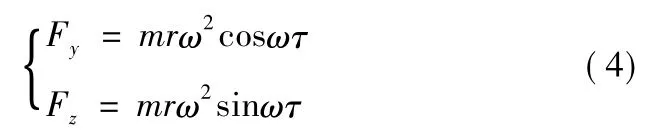
即，相当于在圆盘中心两个相互垂直方向上作用两个简谐力，其相位相差π/2。设定转子转速为2 000 r/min，设置谐响应分析子步数为200，频率范围0 ～200 Hz，分别研究转子轴承系统在承受10 N、15 N 不平衡激励力作用下，对不同转盘位置振动大小的影响及转盘受到同向、反向不平衡力时的振动影响。利用ANSYS 谐响应分析及时间历程后处理器［11］—POST26 查看分析结果，转盘1、2 在不同不平衡激励力下Y 方向的频率响应曲线如图5 ～12 所示。

由图5 ～12 可以看出，转盘1、2 在不平衡激励力作用下，共振频率点基本相同，均在临界转速附近，且在第一阶临界转速附近，转盘1、2 在不平衡激励力作用下的共振幅值最大。由图5 ～10 图对比可以看出随着不平衡激励力的增加，转盘1、2 的不平衡响应幅值也跟着增加。由图9、10 与图11、12 进行对比可以看出，在两个转盘同时施加相同同向或反向不平衡离心力时，施加反向不平衡激励力时的振动幅值小于施加同向不平衡激励力时的振动幅值。由图5 ～8 观察不平衡激励力对转盘1、2 不同位置的响应可以看出，转盘1、2 在受同样的不平衡激励力时，转盘2 对不平衡的响应更为明显，这主要由于转盘1 两端都有轴承支撑，而转盘2 仅仅只有一个轴承的支撑，稳定性较差，受到不平衡激励力时产生的不平衡响应较大。

图5 转盘1 位置施加10 N 不平衡激励力转盘1、2 位置Y 方向频率响应曲线

图6 转盘1 位置施加15 N 不平衡激励力时转盘1、2 位置Y 方向频率响应曲线

图7 转盘2 位置施加10 N 不平衡激励力转盘1、2 位置Y 方向频率响应曲线

图8 转盘2 位置施加15 N 不平衡激励力转盘1、2 位置Y 方向频率响应曲线

图9 同时施加10 N 同向不平衡激励力转盘1、2 在Y 方向频率响应曲线

图10 同时施加15 N 同向不平衡激励力转盘1、2 在Y 方向频率响应曲线

图11 同时施加10 N 反向不平衡激励力转盘1、2 在Y 方向频率响应曲线

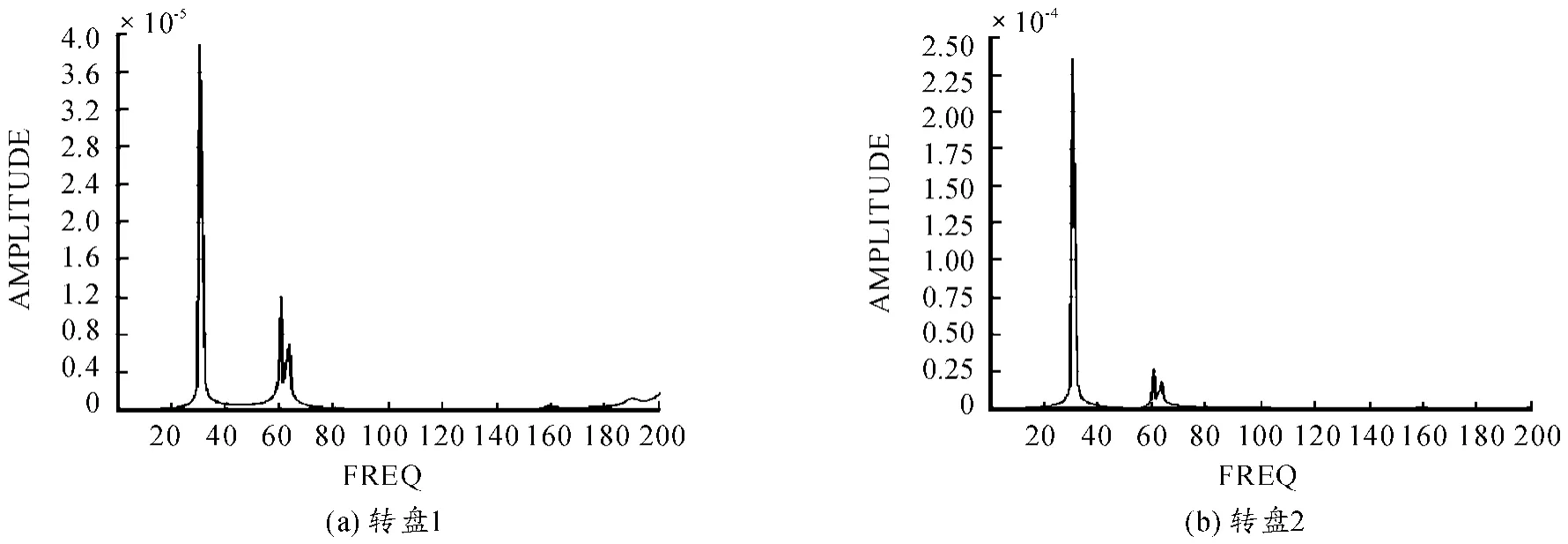
图12 同时施加15 N 反向不平衡激励力转盘1、2 在Y 方向频率响应曲线

4 结论

本文对实际转子轴承系统进行简化处理，利用ANSYS线性离散模型计算规模小、求解速度快的特点对转子轴承系统进行转子动力学建模分析。通过坎贝尔图获得转子系统的临界转速，并进一步对转子系统进行不平衡响应分析，验证了临界转速求解的正确性。通过分析在不平衡激励力下不同转盘上的频率响应曲线，由图5 ～12 可以得出:

1) 转子轴承系统在不平衡激励力作用下，在其临界转速附近具有较大的振动幅值。且随着不平衡激励力的增大，不平衡响应幅值也变大。转子在设计的时候应避免其工作转速在临界转速附近，这样这一减少转子在不平衡量作用下的振动。

2) 转子上存在多个不平衡量时的响应时，有两个同向不平衡量存在时，将会使得响应幅值明显增加; 有两个反向不平衡量存在时，响应幅值有所降低。

3) 转盘1 与转盘2 相比，转盘1 在不平衡激励力作用下的振动幅值较少。转盘1 处于两端支撑的轴承的位置，而转盘2 只有一个轴承支撑，因此具有两端支撑的轴承转盘处的稳定性更好。

由以上转子轴承系统的临界转速和不平衡响应分析实例可知，舰船汽轮机转子的工作转速必须避免在其临界转速附近，以免发生共振产生剧烈振动进而影响舰船航行的安全可靠性。由于舰船汽轮机转子在复杂的多变工况的环境中运行，在舰用汽轮机转子设计时，具有两端轴承支承的转子稳定性更强。同时，舰用汽轮机转子在高温高压下工作，转子产生不平衡量的位置方向复杂多变，有以上实例分析可知，即是有不平衡故障的情况下也会有部分振动相互抵减，影响对故障的监测，因此，舰船在完成航行任务后应及时进行设备检测，及早发现处理隐患，确保汽轮机组的安全，延长使用寿命。

［1］赵常兴.汽轮机组技术手册［K］. 北京: 中国电力出版社，2007.

［2］刘晓东.汽轮机转子临界转速计算分析［J］.装备制造技术，2009(4):59-61.

［3］陈建飞.汽车水泵的强度分析和转子动力学分析［D］.上海:上海交通大学，2012.

［4］张鹏鹰，陈兵，曹跃云，杨自春.模拟转子不平衡响应数值分析及实验研究［J］.海军工程大学报，2000(2):49-53.

［5］朱向哲.转子系统稳态和瞬态不平衡响应的有限元分析［J］.石油化工设备技术，2007，28(2):58-61.

［6］张谦，曹磊.基于ANSYS 的临界转速计算［J］.振动工程学报，2004，17(8):234-237.

［7］Yasuyuki SUZUKI. Unbalance response attenuation of a flexible rotor suspended by magnetic bearings with open loop control［J］. JSME International Journal，Series C: Dynamics，Control，Robotics，Design and Manufacturing，1994(6):285-291.

［8］吴英友，邢维升，朱显明，等.某型离心水泵振动特性分析［J］.中国舰船研究，2008，3(1):51-54.

［9］闻邦椿，顾家柳，夏松波，等.高等转子动力学-理论技术与应用［M］.北京:机械工业出版社，2000.

［10］曾嫣，樊久铭，姚大坤.汽轮机转子动力学建模［J］.电站系统工程，2007(7):27-28.

［11］张洪才，何波.有限元分析——ANSYS13 从入门到实战［M］.北京:机械工业出版社，2011.