装备保障方案的综合权衡分析与优选方法

陈智芳，朱 觅，王卫国

( 中国空空导弹研究院，河南 洛阳 471009)

装备保障方案是装备保障系统完整的系统级描述，在装备设计过程中应同步考虑其保障方案。每一个设计方案可能对应着多个保障方案，如何从这些备选的保障方案中选定较优的方案，是装备综合保障工程的一项重要内容［1］。

然而，当前在选定保障方案时，更多地是根据以往经验或单纯地根据人的主观判断来做出决策，其合理性就得不到保证。

层次分析法是一种非常有效的综合分析方法。它可以将半定性、半定量的问题转化为定量计算，多用于对定性指标的权重分析和方案的选择［2］。本文引入层次分析法，以实现定性分析与定量计算的有机结合，克服单纯由经验或主观因素做出决策的不足，为选定装备保障方案提供参考。

1 层次分析法

层次分析法( Analytic Hierarchy Process，简称AHP) 是20世纪70 年代由美国运筹学家T.L.Saaty 提出来的一种定性分析和定量计算相结合，系统化、层次化的分析方法［3］。其基本原理是:首先将复杂的问题层次化，形成一个递阶的、有序的层次结构模型; 然后根据系统特点和基本原则，对各层的因素进行对比分析。引入1 ～9 标度法构建出判断矩阵，用求解判断矩阵最大特征根及特征向量的方法得到各因素的相对权重;最终通过计算最低层( 方案层) 相对于最高层( 总目标) 的相对重要性次序的组合权重值，以此作为评价和选择方案的依据［4］。

层次分析法分析问题的步骤包括: 建立层次结构模型、构造判断矩阵、计算各层元素对上层元素的相对权重并检验其一致性、推导方案层对系统目标的组合权重向量。

1.1 建立层次结构模型

首先要把问题条理化、层次化，构造出一个有层次的结构模型，一般把研究对象分成3 层，即目标层( G) ，准则层( C) 和方案层( P)［5］。

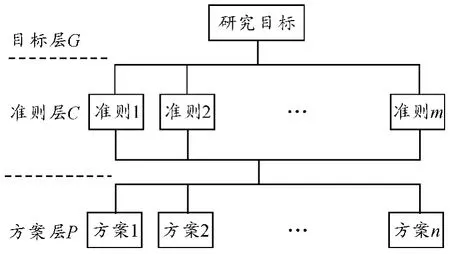
图1 层次结构模型

1.2 构造判断矩阵

为了能把采集到的主观信息进行统一的量化，构造判断矩阵时采用1 ～9 的比例标度将思维判断数量化，保证被比较元素在所考虑的属性上有同一个数量级或比较接近。

表1 1 ～9 标度的定义

对各层元素进行两两比较，可得判断矩阵

式中:r 为各层次的元素个数;矩阵主对角元素的值为1。

1.3 计算特征值和对应的特征向量

对于矩阵A，计算其最大特征值λmax和对应的特征向量W。

由于判断矩阵的建立受各种实际因素和主观倾向的干扰，故需对判断矩阵进行一致性检验。利用一致性比率CR来衡量矩阵的一致性。

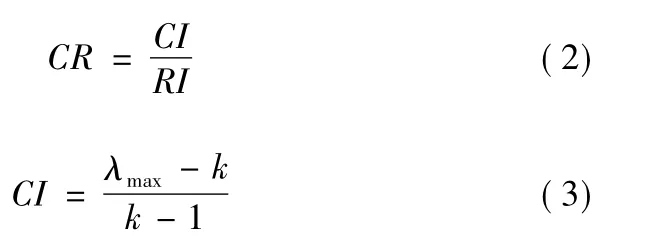
式中:CR 为一致性比率( consistency rate) ，当阶数k≤2 时，判断矩阵具有完全一致性; 当阶数k ＞2 时，如果CR ＜0.1，认为判断矩阵满足一致性要求，否则需要重新调整判断矩阵，直到满意为止; RI 为平均随机性指标( random index) ; CI 为一致性指标( consistency index) ; λmax为最大特征值k 为矩阵的阶数;RI 为多次(500 次以上) 重复进行随机判断矩阵特征值的计算之后取算数平均数得到的。

表2 平均随机一致性指标RI

对W 进行归一化处理，得到的归一化向量即为本层各元素对上层元素的权重向量。

1.4 推导方案层对系统目标的组合权重向量

方案层对系统目标的组合权重向量

式中:WPC为方案层对准则层的权重向量;WCG为准则层对目标层的权重向量。WPG是一个一维向量，其元素wj( j =1，2，…n) 为方案Pj对研究目标的相对权重，可以对wj进行排序来获得方案层各元素的重要次序［6］。

2 装备保障方案的综合权衡分析与优选

现以某型装备为例，说明层次分析法在装备保障方案选定过程中的应用。对应于该装备的设计方案，有2 个备选的保障方案可以对其实施有效的保障:方案1 为3 级维修保障方案，方案2 为2 级维修保障方案。由于在初期缺乏足够有效的数据，所以，采用层次分析法来对这两个保障方案进行评价，以便选出更好的保障方案。

方案1:实施3 级维修体制，即外场级、内场级和工厂级。对于该保障方案而言，需要一定数量的专用保障设备，而且复杂程度也比较高; 需要一定数量的专用器材，但供应的复杂程度比较低;需要几个新的技术专业，但对人员技能要求比较高;需要培训的人员数量不是很多，培训时间也不是很长，但需要一定数量的训练设备才能保证完成训练任务; 只需要新建中等数量的设施即可满足要求;需要一定数量的嵌入式计算机，软件保障工作负责程度属于中等; 需要开发包装、装卸、贮存方法和研制少量的新设备;需要的技术资料数量比较多，但编写难度小。

方案2:实施2 级维修体制。此保障方案中，需要大量的专用保障设备，复杂程度属于中等;需要少量的专用器材，但供应的复杂程度高; 需要较多的新技术专业，但对人员技能要求比较低;需要培训的人员数量很多，培训时间比较长，而且还需要一定数量的训练设备才能保证完成训练任务;需要新建大量设施才能满足装备的要求;需要较少的嵌入式计算机，软件保障工作复杂程度不算太高; 需要开发包装、装卸、贮存方法和研制少量的新设备; 需要的技术资料数量比较多，编写难度属于中等。

根据前面给出的方法，对方案1( P1) 和方案2( P2) 进行综合权衡分析如下。

2.1 建立递阶层次结构

图2 层次结构

2.2 判断矩阵与矩阵的一致性检验

方案P1和P2相对于准则层各元素Ci( i=1，2，…，8) 的比较判断表如表3 ～10 所示。

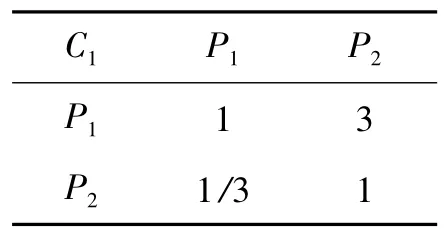
表3 P1 和P2 相对于C1 的比较判断表

表4 P1 和P2 相对于C2 的比较判断表

表5 P1 和P2 相对于C3 的比较判断表

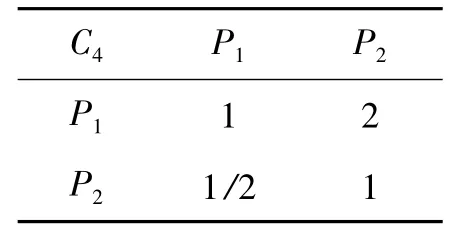
表6 P1 和P2 相对于C4 的?比较判断表

表7 P1 和P2 相对于C5 的比较判断表

表8 P1 和P2 相对于C6 的比较判断表

表9 P1 和P2 相对于C7 的比较判断表

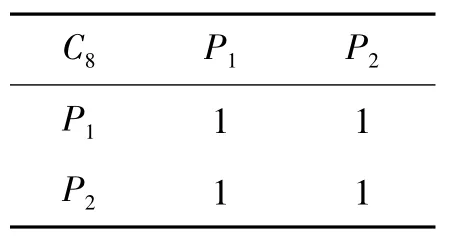
表10 P1 和P2 相对于C8 的比较判断表

以P1和P2相对C1为例，其判断矩阵为，求得最大特征值λmax1= 1. 999 9，对应的特征向量wPC1=[0.948 7 0.316 2 ]T，归 一 化 处 理，得 到 WPC1=[0.750 0 0.250 0 ]T，判断矩阵为2阶矩阵，满足一致性。

同理，可得

1) λmax2=2，对 应的特征向量wPC2=[0.447 2 0.897 4 ]T，归一化处理，得到WPC2=[0.3326 0.6674]T。

2) λmax3=1.9999，对应的特征向量wPC3=[0.948 7 0.316 2 ]T，归一化处理，得到WPC3=[0.75000.2500]T。

3) λmax4=2，对应的特征向量wPC4=[0.89740.4472]T，归一化处理，得到WPC4=[0.6674 0.3326]T。

4) λmax5=2，对应的特征向量wPC5=[0.8974 0.4472]T，归一化处理，得到WPC5=[0.6674 0.3326]T。

5) λmax6=1. 9999，对应的特征向量wPC6=[0.9487 0.3162]T， 归一化处理，得到WPC6=[0.7500 0.2500]T。

6) λmax7=1. 9999，对应的特征向量wPC7=[0.3162 0.9487]T， 归一化处理，得到WPC7=[0.2500 0.7500]T。

7) λmax8=2，对应的特征向量wPC8=[0.7071 0.7071]T，归一化处理，得到wPC8=[0.5000 0.5000]T。

方案层元素P1和P2相对于准则层( C 层) 各元素的判断矩阵均为2 阶矩阵，均具有满意的一致性。

准则层( C 层) 相对于目标层( G 层) 的比较判断表如表11 所示。

求得最大特征值λmax=8.309 7，对应的特征向量

wCG= [-0.579 4 -0.085 2 -0.166 5 -0.363 5-0.640 9 -0.259 5 -0.063 9 -0. 122 7 ]T

归一化处理，得到

WCG= [0.253 9 0.037 4 0.073 0 0.159 3 0.280 9 0.113 7 0.028 0 0. 053 8]T

则

即判断矩阵具有满意的一致性。

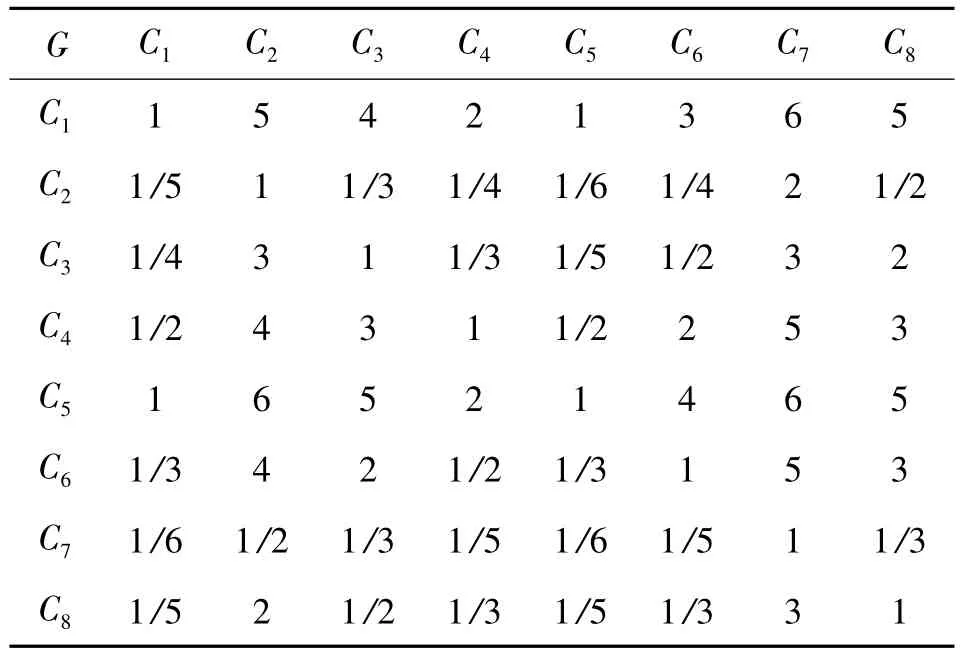
表11 准则层( C 层) 相对于目标层( G 层) 的比较判断表

2.3 推导方案层对最终目标的组合权重向量

根据上文可得:

则，P 层对G 层的组合权重向量为

即方案P1和P2对最终目标的排序为P1，P2，故方案P1为优选的最终方案。此结果与当前通常采用的3 级维修体制相一致，也验证了此方法是合理的、有效的。

3 结束语

本文提出的方法将定性与定量有机结合，既考虑了专家的专业知识和工程应用经验，又将综合结果进行了量化处理，结果清晰明了，可以为选定较优的装备保障方案提供参考。然而，采用该方法时，需要参与决策的专家具有扎实的专业知识和工程应用经验，以保证判断矩阵的合理性。为此，需要适当扩大专家咨询范围，以增大采集的样本量并进行相应处理，从而保证结果的合理性和可信性。

［1］刘东，李东，杨海涛.装备综合保障技术［J］.国防科技，2009(6):45-52.

［2］杜栋，庞庆华.现代综合评价方法与案例精选［M］.北京:清华大学出版社，2005.

［3］刘新宪，朱道立.选择与判断——AHP( 层次分析法) 决策［M］.上海:上海科学普及出版社，1990.

［4］许树柏.实用决策方法——层次分析法原理［M］.天津:天津大学出版社，1988.

［5］李建峰，郑永伟，李彬.地铁车站施工方案优选决策模型［J］.西安科技大学学报，2009(2):159-164.

［6］黄玉刚.层次分析法在施工组织设计方案比选中的应用［J］.铁路工程造价管理，2012(1):24-27.

［7］崔大连，周爱军.AHP 方法在装备保障方案权衡分析中的应用［J］.四川兵工学报，2010(3):44-46.

［8］陈校平，车飞.装备保障能力的动态评估［J］.火力与指挥控制2011(7):167-170.