周转斜盘发动机运动学建模与仿真

李云志，梁伟阁

(1. 92474 部队装备部，海南 三亚 572018; 2.海军工程大学 兵器工程系，武汉 430033)

斜盘发动机是采用空间斜盘结构的一种特殊的活塞发动机，其结构简单紧凑，功率质量比大，适用于大深度工作的水下航行器［1］。发动机燃料在燃烧室中生成高温高压气体，并经配气机构将高温高压气体分配至各气缸，推动活塞进行往复运动，而空间连杆机构将活塞的往复运动转换成输出轴的旋转运动，从而驱动水下航行器的推进器，使其获得航行时所需的动力。因此，有必要开展对水下航行器斜盘发动机运动学的分析。

针对周转斜盘发动机工作过程，学者王国治、薛运锋等从动力学角度入手，运用虚拟样机技术，对周转斜盘发动机的运动过程进行了仿真计算［2-4］;朱拥勇博士则从动力平衡角度分析了周转斜盘发动机振动力和振动力矩，并对其平衡进行了优化计算［5-7］;而Manring 等学者则针对周转斜盘机具体结构参数斜轴直径和力矩大小进行了详细分析，并计算得到这些参数的合理范围［8-9］。然而，对周转斜盘发动机动力、平衡及结构参数的计算仿真均离不开对其运动学的分析。本文基于周转斜盘发动机活塞和连杆运动模型，结合模型仿真，对其运动过程进行仿真分析，以期对发动机动力学分析、平衡性能分析等有一定的参考意义。

1 主要结构参数

如图1 所示，周转斜盘发动机的主要结构参数有: 气缸分布圆半径Rg，是缸体上均布的各气缸中心线的圆柱半径;后球心圆半径Ra，是斜盘上连杆后球头球心的圆半径; 斜盘倾角α，是缸体轴线与斜盘转动轴线的夹角; 连杆长度lg，是连杆前后球头球心的距离;轴向位移ξ，是后球心圆所在平面到顶点( 周转斜盘轴线同缸体轴线的相交点) 的距离;周向位移χ，是指连杆前球心在转角上超前于后球心的数值，即χ =ψ-θ( ψ、θ 分别代表连杆前球心转角、后球心转角) ; 滚轮后置角γ，是指周转斜盘上滚轮轴线与基准后球心所在的后球心圆半径线构成的圆心角。

图1 斜盘发动机主要结构参数

2 单位连杆向量

取右手直角坐标系o -xyz 和o' -x2y2z2，如图1 所示。两坐标系的原点分别置于顶点和后球心圆圆心，z 和z2轴置于分界平面上，x 和x2轴分别置于缸体轴线和周转斜盘轴线上，y 和y2轴互相平行。设单位连杆向量为e，其沿各坐标系的分量分别为X(ψ) 、Y(ψ) 和Z(ψ) ，经过推导、整理，得到如式(1)［1］:

这里用无因次结构参数表示单位连杆向量，如式(2) :

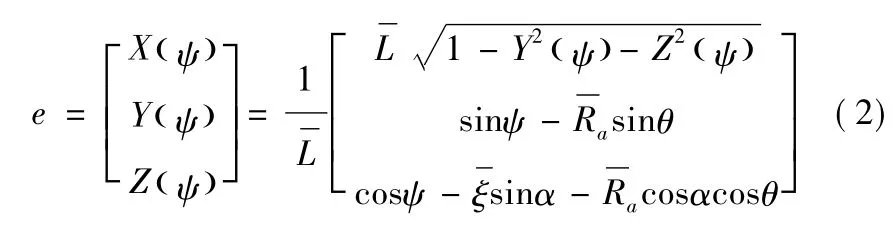
由式( 2) 可得单位连杆向量对前球心转角ψ 的一次变率:

3 活塞运动模型

由于连杆前球与活塞相铰联，因此连杆前球心b 的运动实际上代表了活塞沿气缸轴线的运动。这里主要讨论活塞的位移、加速度和速度的变化。

3.1 活塞运动位移

活塞沿气缸轴线运动的极前和极后位置分别称为前止点和后止点。设ψq、ψh及θq、θh分别为活塞处于前、后止点时连杆前、后球心的转角。经过分析、推导，可得活塞的冲程S 为前球心轴向坐标的极大值Xobmax和极小值Xobmin之差，即

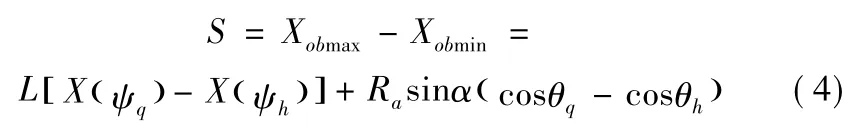
活塞位移s 是前止点到其瞬时位置的距离，相当于前球心轴向坐标的极大值Xobmax与瞬时值Xob之差，即

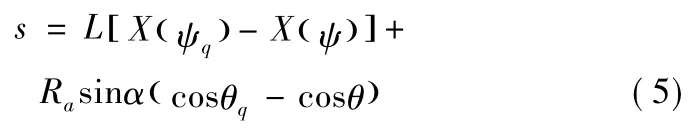
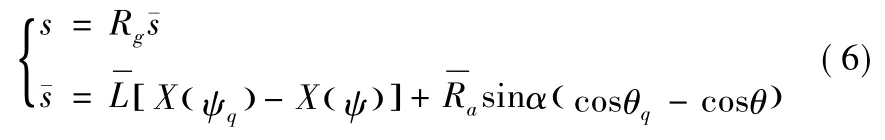
3.2 活塞运动速度

活塞位移对时间的导数即为活塞的速度，故有

其中ω 表示发动机转动角速度，若以¯v表示活塞运动无因次速度，则上式可表示:

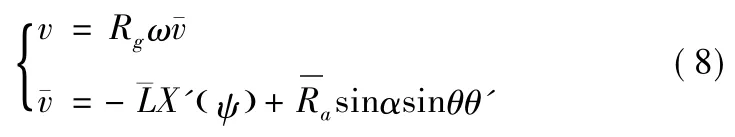
3.3 活塞运动加速度

活塞运动速度对时间的一次导数即为其运动加速度，若以¯a 表示活塞的无因次加速度，则:

4 连杆运动模型

周转斜盘发动机工作时，连杆作空间运动，这种运动包括连杆相对于前球心的运动和相对于后球心的运动。

4.1 连杆相对于前球心的运动

在过顶点o 的缸体横断面上取一个坐标系o1-x1y1z1，其原点o1在气缸轴线上，z1轴通过顶点o，如图2 所示。设负单位连杆向量-e 在o1-x1y1z1坐标系中的分量分别为X1( ψ) 、Y1( ψ) 、Z1( ψ) 。后球心相对于前球心的运动轨迹在一个球面上，它在缸体横断面上的投影在y1、z1坐标方向上的无因次分量可表示:

由式(18) 可知，后球心相对于前球心的运动是由两种运动叠加起来的。第一种运动由上式的第一项表示，是周向位移和轴向位移引起的无因次半径为的圆周运动，称为一次谐振运动。第二种运动由上式的第二项表示，其是由周转斜盘倾角引起的无因次半径为的圆周运动，称为二次谐振运动。上式中的第三项称为谐振中心，后球心的一次谐振运动和二次谐振运动是围绕谐振中心进行的。

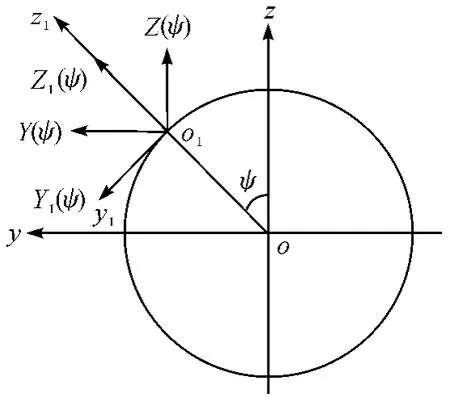
图2 o1 -x1y1z1 坐标系

连杆运动时，其轴线绕前球心作锥面运动，由连杆运动引起前球轴承内的相对滑动速度可由下式计算得到:

式( 19) 中Rzq是指连杆前球头半径; ω 表示发动机转动角速度。

4.2 连杆相对于后球心的运动

为了得到后球心的相对滑动速度，先将单位连杆向量变换至o' -x2y2z2坐标系中，即

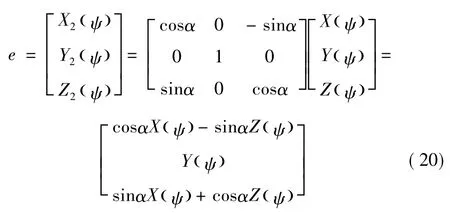
对其进行求导运算，可得连杆后球轴承内的相对滑动速度:

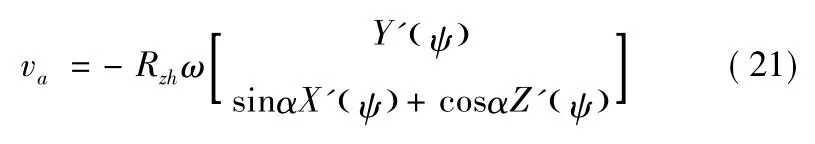
式(21) 中Rzh是指连杆后球头半径。

5 仿真分析

基于某型斜盘发动机结构设计参数，依次对单位连杆向量变化趋势、周向位移的变化趋势、活塞的运动参数变化趋势及连杆的运动情况进行仿真分析，可以得到以下仿真结果。

5.1 活塞的运动参数仿真

图3 -图5 为发动机6 个活塞的位移、速度及加速度在一个冲程内的变化曲线，表1 所示为活塞位移、速度及加速度的最大值。

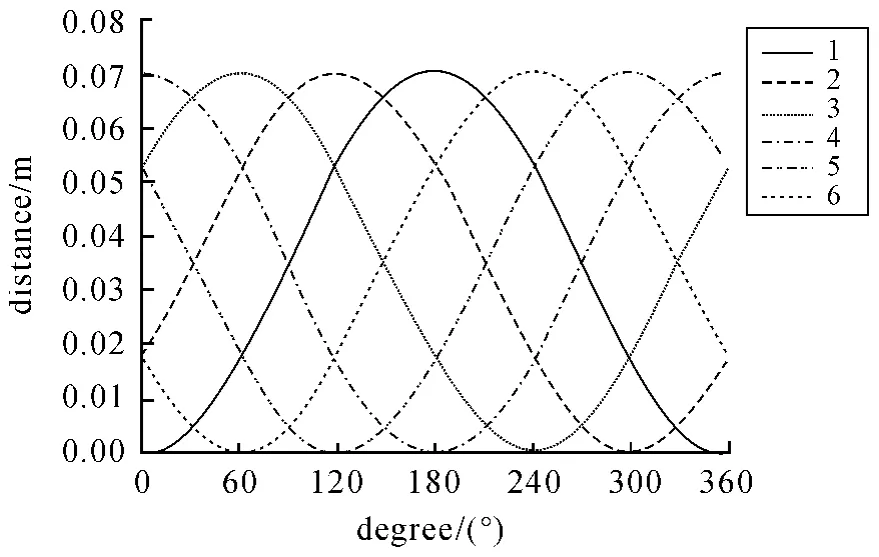
图3 活塞的位移变化曲线

图4 活塞的速度变化曲线

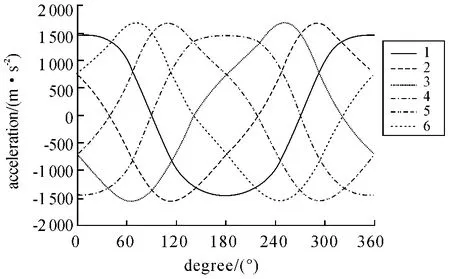
图5 活塞的加速度变化曲线

经过分析可知，发动机6 个活塞连杆机构的运动规律不一，周向相隔180°的气缸，即第1、2、3 气缸分别与第4、5、6气缸的运动规律一致，1 气缸与3 气缸的运动规律存在这样的函数关系:X( x1) =X(360° -x1) 。

活塞的运动近似为简谐运动，在误差允许的范围内，位移最大值，即活塞的冲程均约为70.456 mm，而活塞1(3) 的最大速度大于其他活塞的速度，但是其加速度却小于其他活塞的加速度。活塞速度和加速度的数值差异会影响发动机的平稳运动，数值差越大，发动机运行越不平稳。

表1 活塞的位移、速度和加速度的最值

5.2 连杆运动仿真

由于连杆作空间运动，且主轴方向( x 向) 的运动对发动机的平稳运行无不良影响，而其他两个方向( y、z 向) 的运动则会引起发动机的振动，因此在此主要对y、z 方向的连杆运动进行仿真分析。由前面的分析可知第1、2、3 气缸分别与第4、5、6 气缸的运动规律一致，因此这里可仅对第1、2、3 连杆进行运动分析，第4、5、6 连杆的运动状态与之相同。

由图6 和图7 可知，连杆相对于前球心的运动曲线属振幅为±0.5，周期为180°的简谐曲线，连杆的运动过程相对较平稳。而连杆相对于后球心的运动曲线却不严格符合简谐运动的规律，运动速度的抖动较为明显。因此，连杆相对于后球心的不平稳运动可能形成发动机运转的新的振源，进而带来振动噪声。由于连杆相对于后球心的运动在Y 方向的抖动幅度要大于其在Z 方向的抖动幅度，因此，这种不平稳运动主要由Y 方向速度的不稳定造成的。

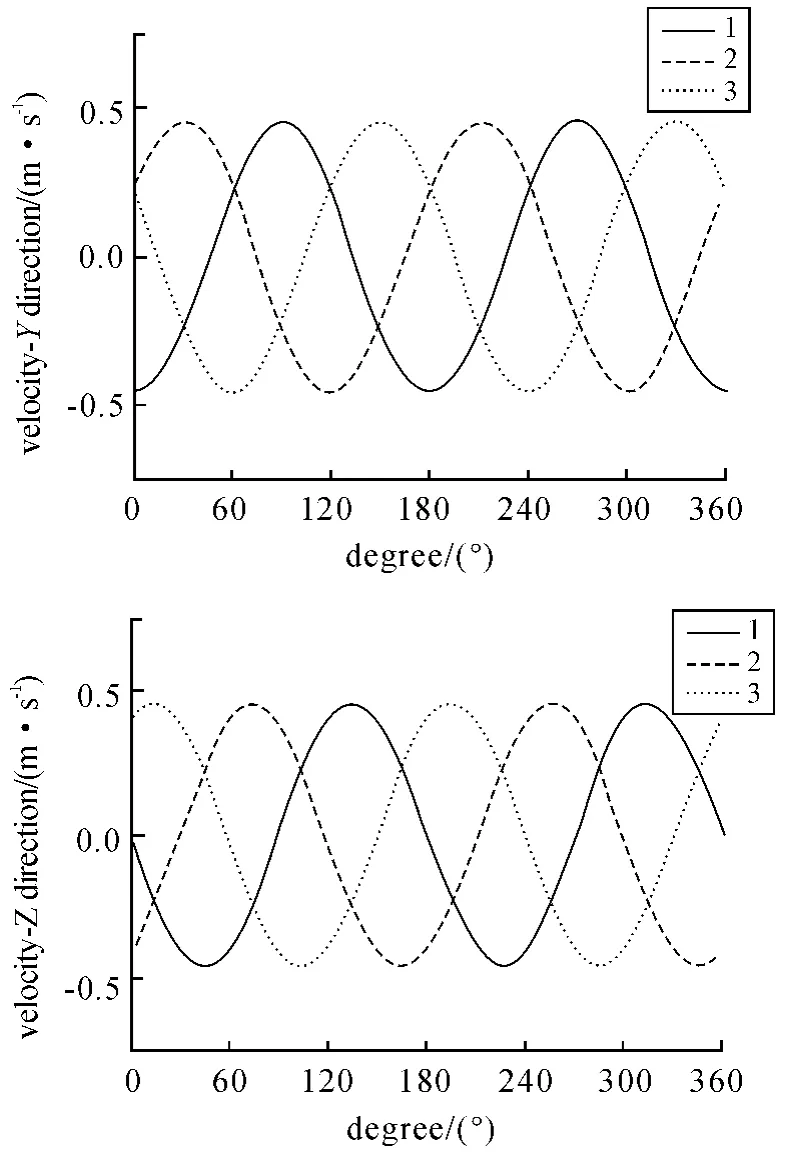
图6 连杆相对于前球心的运动曲线

图7 连杆相对于后球心的运动曲线

6 结论

针对周转斜盘发动机的工作过程，建立了其活塞和连杆的运动模型，并结合某型周转斜盘发动机的具体参数，仿真分析了发动机活塞的运动参数和连杆的运动速度的变化，经过讨论，主要得到以下结论:

1) 活塞的运动速度和加速度较平稳，但是不同的活塞则具有不同的速度和加速度，即活塞组运动处于不平稳状态，形成了发动机工作的一个振源。

2) 连杆相对于后球心的不平稳运动速度则是发动机工作的另一个振源，且Y 方向的不平稳运动速度对这种不平稳运动的贡献较大。如何改变这种不平稳运动则是我们下一步的研究内容。

［1］马世杰.热动力装置设计原理［M］.北京:兵器工业出版社，1992.

［2］郑学贵，王国治.斜盘发动机虚拟样机的动力学仿真分析［J］. 华东船舶工业学院学报: 自然科学版，2004，18(4):81-85.

［3］王国治，洪炉，张栋.摆盘发动机的虚拟设计与运动仿真［J］.中国机械工程，2006，17(21):2252-2256.

［4］薛运锋，石明全，陈维义.基于ADAMS 的某发动机动态仿真［J］.弹道学报，2006，18(6):49-52，56.

［5］朱拥勇，王德石，邵松世.摆盘发动机动力平衡的优化设计［J］.机械强度，2007，29(4):593-597.

［6］朱拥勇，王德石，严侃.摆盘发动机空间机构的震动力完全平衡研究［J］. 舰船科学技术，2007，29( 1): 41 -43，52.

［7］朱拥勇，王德石.摆盘空间机械振动力与振动力矩完全平衡研究［J］.中国机械工程，2008，19(11):1343-1347.

［8］MANRING N D.Designing the shaft diameter for acceptable levels of stress within an axial-piston swash-plate type hydrostatic pump［J］. Journal of Mechanical Design，2000，122:553-559.

［9］MANRING N D，Damtew F A. The control torque on the swash plate of an axial-piston pump utilizing piston-bore springs［J］.Journal of Dynamic Systems，Measurement，and Control，2001，123:471-480.