水下射弹自然超空泡特性数值模拟与试验

赵潇雨

( 海装驻重庆地区军事代表局，重庆 400042)

超空泡减阻是1 种使水下航行体保持高速航行的创新途径。其基本原理是利用航行体表面形成的气层使周围液体与航行体表面相隔离，减少其沾湿面积，从而大幅降低航行体的黏性阻力。随着高新技术的不断发展，水中兵器对于水面舰艇的威胁日趋严重［1］，将超空泡减阻技术运用到小口径炮弹上，提高水面舰艇对鱼雷、水雷等水中目标的水下近程主动防御能力，已成为各国海军弹药发展的方向之一［2］。

根据空泡的生成方式，超空泡可分为通气超空泡和自然超空泡2 种。其中，自然超空泡主要利用航行体自身的高航速形成气体包层，并通过空化器设计控制空泡形态，主要适用于水下枪弹以及超空泡炮弹等高初速、小尺度超空泡武器［3-4］。在超空泡技术研究中，产生与航行体外形结构相匹配的稳定超空泡包层是研制超空泡武器的关键。本文利用CFD 计算软件Fluent6.3，通过数值计算，对一型水下超空泡射弹在一定空化数范围内的超空泡特性，以及空化器设计与弹形尺寸匹配性进行了研究分析，并在此基础上，进行了水下射弹试验，对弹形结构设计的匹配性和计算模型的合理性进行了验证。

1 数学模型

1.1 空泡流模型

采用气液两相流模型来模拟水下航行体的空泡流动，将水/汽两相混合流作为密度可变的单一流体来处理，混合流之间不存在分界面，整个混合物允许相互对流，对混合物的连续方程和动量方程进行求解。

混合相的连续方程为

其中

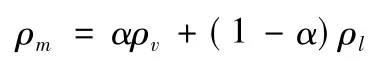
式中:ρm为混合相密度为混合相质量平均速度; α 为蒸汽体积比;ρv为气相密度;ρl为液相密度。

混合相的动量方程为

其中

式中:μm为混合相的黏度;μv为气相黏度;μl为液相黏度。

由于水下航行体壁面附近液体会出现1 个液态转化为气态的过程，在空化模型的数值模拟过程当中，要考虑气泡中气相和液相的质量交换。Rayleigh-Plesset 方程提供了1 个将气泡动力学影响引入空泡流的物理模型，反映了气泡的膨胀和收缩过程，该方程表达式为

式中:R 为气泡半径;pB为气泡内压力; pv为蒸汽部分压力;σ 为表面张力系数。

1.2 湍流模型

引入标准的k-ε 混合湍流模型:

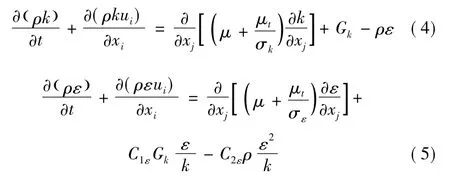
其中:μt是湍流黏度是由于速度梯度引起的湍流动能产生项，对于模型常数为经验常数;σk、σε分别是湍流动能和耗散率对应的Prandtl 数。常数的取值，选择Fluent 软件的推荐值，分别为:C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。

采用非平衡壁函数( non-equilibrium wall functions) 处理近壁区域。

2 计算模型及数值方法

超空泡射弹模型的主要结构尺寸参数为: 弹丸长194 mm，头部采用平头空化器设计，空化器尺寸为Φ4 ×3.8mm;弹体圆柱部直径为Φ12.8mm。在二维和三维建模过程中，均使用结构化网格。在弹轴与来流速度方向一致的情况下，认为整个流场沿弹轴成对称分布［5］，对二维计算模型采用了轴对称处理，对三维计算模型采取了1/4 面对称处理。二维流场的外边界为1 000 mm×2 800 mm，三维流场的外边界为Φ2 000 mm×2 800 mm。入口边界采用速度入口，出口边界给定压强。同时，为使计算模型在计算精度和计算效率上得到较好平衡，在该模型网格数量控制以及分布设计上，对于弹体近壁面以及棱角处等流体情况变化很大的区域，采取网格加密的策略，而在离弹丸较远的流场则对网格尺寸进行了适当放宽的方案。建模后二维模型外流场网格数量约为4.3万个，三维模型外流场网格数量约为50 万个。

二维流场网格分布以及弹壁附近网格情况分别如图1、图2 所示。图1 中，流场左侧、上侧和下侧边界为速度入口，右侧边界为压力出口。

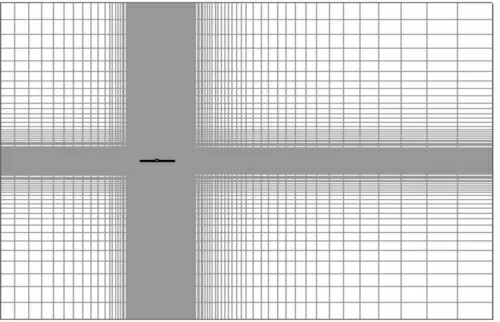
图1 二维流场网格分布

图2 弹壁附近流场网格分布

三维流场网格以及弹丸表面网格分布情况分别如图3、图4 所示。图3 中，圆柱体左侧以及立柱面为流场速度入口，右侧底面边界为流场压力出口。

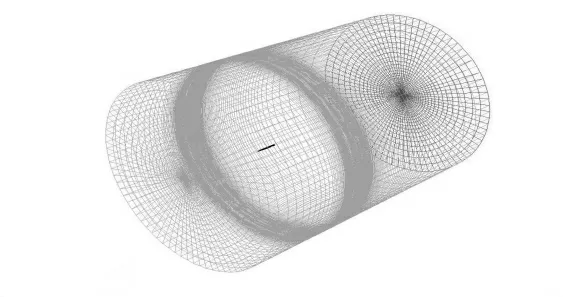
图3 三维流场网格分布

图4 三维弹丸网格分布

选择非耦合隐式求解器，将水作为1 种不可压缩流体处理。由于模型解算过程中包含液相随着压降相变为气相的过程，流体包含了气、液两相，因此使用带有空化作用的混合相模型。压力与速度之间的耦合求解采用SIMPLE 算法，由于该计算模型的网格划分已经比较密，为了不使运算过程的解发生振荡，空间离散选择一阶迎风格式。

3 计算模拟分析

3.1 超空泡生成与发展模拟

采用了非定常方法对超空化流动进行求解，以捕捉弹丸在零攻角情况下入水后，空泡的生成发展过程。弹丸在入水速度为200 m/s 时空泡的生成发展过程如图5 所示。

图5 水下射弹在速度为200 m/s 的超空泡发展过程

通过数值计算可以看出，弹丸在入水后，将首先在空化器附近以及弹丸尾部瞬间形成2 个小空泡，随着时间的推进，空泡迅速扩大、汇合、再扩大，最后形成1 个稳定的自然超空泡。图6 显示了弹丸以200 m/s 速度入水后，黏性阻力系数的变化情况。射弹在入水后，随着空泡的生成、发展，弹丸受到的黏性阻力系数迅速降低，当整个空泡完全覆盖在弹体表面形成超空泡后，黏性阻力系数接近为零。

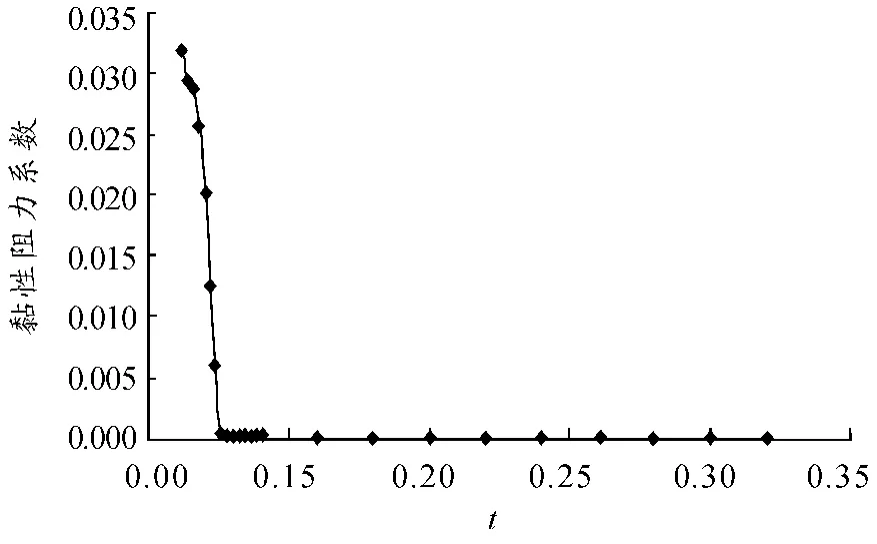
图6 射弹在200 m/s 速度入水时黏性阻力变化曲线

3.2 超空泡流场数值模拟

图7 空化器头部附近压力云图

通过数值模拟计算得到射弹在空化数为0.005 0 时，弹体周围以及空化器头部附近的流场迹线，如图8 所示。

通过数值模拟计算得到射弹在空化数为0.005 0 时，空化器头部附近流场速度矢量图，如图9 所示。

图8 空化器头部附近流场迹线图

图9 空化数为0.005 0 时，空化器头部附近流场速度矢量图

通过数值模拟计算得到射弹在空化数为0.005 0 时，流场的气液两相分布，如图10 所示。

图10 空化数为0.005 0 时，计算流场气液两相分布

从图7 ～10 可以看出，弹丸在水下高速航行时，空化器部分将承受很高的水动载荷，同时自头部产生呈球冠形向外扩散的高强度的水( 或汽) 冲击激波。形成稳定超空泡流后，弹体表面包裹一层薄薄的汽泡，弹尾部有1 个拖曳状的较大椭球体汽泡，形成1 个稳定的空化状态区域。表1 给出了该型射弹的运动参数与空泡形态参数的仿真计算结果。从表1中可见，该型射弹虽然在空化数不同的情况下，所形成的超空泡几何外形变化显著，但是始终保持较大的长细比，表明该型射弹所形成的超空泡具有较高形态优良率。

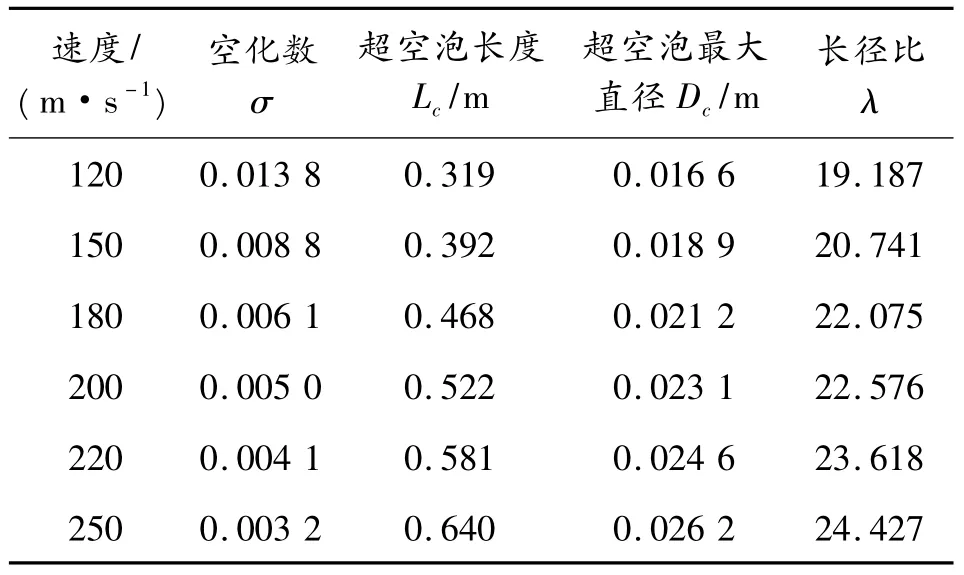
表1 射弹运动参数与超空泡形态参数的仿真计算结果

3.3 超空泡尺寸与弹丸形状匹配性分析

图11给出了空泡的几何特性意义，其中h 为空泡厚度。该型射弹在不同空化数条件下，弹体表面空泡厚度的仿真结果如图12 所示。

图11 空泡径向剖面示意

由图12 可见，在整个稳定超空泡的运动状态范围内，随着射弹速度递减带来的空化数增加，弹体表面各位置的空泡厚度均在不断减小。就整个弹丸而言，射弹尾部位置空泡厚度变化最大，圆柱部在接近临界空化数时空泡厚度最小。其中，在空化数为0.031 8( 在常温、常压下所对应的速度为120 m/s) 时空泡几乎与弹体表面相接触，约为该型射弹超空泡的临界空化数。可以预见，如果射弹的速度继续降低，弹丸的圆柱部和尾翼将最先沾湿，射弹表面超空泡将在这些部位开始剥离脱落，随后将迅速溃灭、消失。

3.4 射弹减阻特性比较

为比较该型射弹在超空泡技术应用后的减阻特性，模拟计算时，在不同空化数下对有空泡与无空泡情况下的阻力系数进行了比对，如表2 所示。

通过表2 可以看出，超空泡技术的运用，不仅可使黏性阻力的减阻率达到99.9%，还可大幅降低压差阻力系数。

表2 有空泡情形和无空泡情形的阻力系数对比

4 实弹射击试验

本文利用轻气炮通过气压产生弹丸初始动能，进行单发实弹平射射击。弹丸在空中实现弹托分离，弹芯以高速通过专用试验水槽，利用高速摄像观测弹丸在入水前的速度、水下的运动姿态以及运动过程中空泡的生成情况。

图13展示了试验过程中拍到的弹丸在不同速度( 即不同空化数下) 空泡生成状态的高速摄像照片。

经试验照相测量，在射弹速度为140 m/s 时，弹径最大处超空泡包层厚度在2 ～3 mm，而在相同空化数条件下，通过数值计算得到射弹在该部位的超空泡包层厚度为2. 4 mm，计算数据与试验结果符合较好。试验结果汇总如表3所示。

表3 实弹射击试验结果

图13 射弹在不同空化数下产生的超空泡

5 结束语

数值计算和射弹试验研究结果表明，该型水下射弹空化器设计与弹形尺寸匹配较合理，在一定空化数条件下能够产生稳定的自然超空泡，所形成的超空泡在迎流面弹体与空泡壁面能够保持很小距离，较好地控制了弹丸所受到的压差阻力，其临界空化数在0.010 1 ～0.024 5;通过对弹丸在水中航行姿态和航行距离的观测可知，该型射弹水下弹道较稳定，没有出现偏航现象，超空泡射弹水中航行减阻效果明显，能较大幅度提高水下高速运动过程的存速能力与航行距离;将试验所得到的超空泡尺寸、临界空化数数值与计算结果进行比较知，计算数据与试验结果吻合较好，验证了本文所建模型的合理性，对水下射弹结构设计研究具有一定的指导意义。

［1］付欣，张静远，高永琪，鱼雷制导与控制发展的回顾与展望［J］.舰船科学技术，2007(10):48-50.

［2］傅金祝，超空泡对未来水中兵器系统的挑战［J］.水雷战与舰船防护，2002(2):18-23.

［3］姚养无，从水下枪械到两栖枪械的历史跨越［J］.轻武器，2003(4):8-10.

［4］傅金祝，美国的快速机载灭雷系统［J］.水雷战与舰船防护，1998(4):41.

［5］Inor Nesteruk.To The Prpblem Of Drag Reduction In High Speed Hydrodynamics［J］. High Speed Hydrodynamics，2002:7-7P.

［6］李东旭.水下超空泡高速射弹数值分析与试验［J］.四川兵工学报，2011(10):25-29.

［7］赵潇雨，周维.自然超空泡形态特性的数值模拟［J］.四川兵工学报，2010(12):49-52.