固体推进剂/衬层界面裂纹的指数型分层界面层模型①
2012-07-09杨月诚
邸 克,杨月诚
(第二炮兵工程大学601室,西安 710025)
固体推进剂/衬层界面裂纹的指数型分层界面层模型①
邸 克,杨月诚
(第二炮兵工程大学601室,西安 710025)
建立了固体推进剂/衬层界面裂纹的指数型分层界面层模型,该模型将界面层划分为多个子层,并在每一子层中用指数函数表示界面层初始模量的分布。应用Fourier变换方法推导出一个Cauchy型奇异积分方程组,采用配点数值方法得到平面应力状态下裂纹问题的半解析解,并讨论了法向和剪切应力加载下界面层参数对应力强度因子的影响。结果表明,界面层模量降低时,应力强度因子的绝对值显著减小;界面层厚度对应力强度因子的影响相对不明显。
固体推进剂;衬层;界面层;分层模型;裂纹;应力强度因子
0 引言
固体推进剂/衬层粘结界面是固体发动机的一个薄弱环节,是影响发动机结构完整性的关键因素,该类界面的裂纹问题更是学者们关注的热点。在这一领域,人们主要采用了有限元数值方法[1-2]或实验研究[3],获得了界面断裂参量及影响裂纹扩展的因素。但这类界面裂纹的理论分析却未见报道,界面粘结结构对裂纹宏观方面的影响也未曾获取。因此,很有必要构建一个合适的推进剂/衬层界面力学模型,并深入开展其裂纹问题的理论研究。
为了合理简化界面结合部,有效研究界面断裂问题,人们提出了许多界面力学模型,如理想界面模型[4]、接触界面模型[5]和无滑动区界面模型[6]等。而对于真实的NEPE推进剂/衬层界面,吴丰军等[7]采用纳米压痕仪和超声波扫描显微镜,证明了其粘结界面层是模量和硬度呈现梯度变化的非均匀结构。因此,表征推进剂/衬层界面断裂问题时,选择Delale和Erdogan[8]提出的功能梯度界面层模型(也称为非均匀界面层模型)是合适的。这种界面层模型将界面粘结区域看成功能梯度材料(FGM),并充分考虑了界面粘结处材料的细观结构对宏观力学性能的影响。此后,人们采用某一种特定的函数表征界面层力学属性的变化,如幂律函数[9]和倒数函数[10]等。另外,相对上述单层界面层模型,Li提出了互扩散界面层模型[11],即将界面层分成2层,用2种函数表示其模量的变化。最近十几年,人们发展了一类FGM分层模型,即将界面层(或涂层)分成多个子层,每一子层中用某种函数表示材料属性的变化。对于垂直于FGM属性梯度方向的裂纹问题,人们在每一子层中采用了常数[12]、线性函数[13]和倒数函数[14]表征FGM属性变化。这类分层模型对于描述FGM属性在空间上任意变化方面具有很大优势。
为了能真实准确地表征推进剂/衬层界面粘结区域材料属性的任意分布,本文为其建立了一个新的指数型分层模型。通过推导并数值求解Cauchy型奇异积分方程组,得到裂纹问题的半解析解,并讨论Ⅰ和Ⅱ型应力强度因子随界面层有关参数的变化规律。
1 指数型分层界面层模型
如图1所示,该模型将界面层划分成N个厚度相等的子层,每一子层中均采用指数函数逼近真实的模量,其中各子层下端面的高度值分别是hk(k=1,2,…,N)。模型中约束衬层上端面的位移,并在界面层第m个子层下端面处设置一长度c=2a,平行于x轴的裂纹。衬层和界面层均看成无限长的条状结构,厚度分别为hL和h0,推进剂的长和高均为无限大。其中,界面层厚度h0表示衬层本体和推进剂本体之间的模量变化区域总厚度。假设模型中各层粘弹性材料的松弛模量(y,t)均可写成初始模量Ek和时间因子f0(t)相乘的形式:
在求解该类问题时,一般应用FGM的粘弹性对应原理[15],先按照弹性理论求得对应的弹性解,再转化为粘弹性解。

图1 固体推进剂/衬层界面的指数型分层界面层模型Fig.1 Exponential multi-layered interfacial zone model for the solid propellant/liner interface
假设衬层和推进剂的初始模量分别是常数E0和EN+1,界面层各子层中采用近似模量Ek(y)(k=1,2,…,N)逼近真实模量Er(y)。其中,Ek(y)为连续的指数型分段函数,并在各子层下端面(y=hk)处Ek(y)和真实模量Er(y)相等,即

此外,假设衬层和推进剂的泊松比分别是常数ν0和νN+1,界面层每一子层中近似的泊松比为νk(y),且在子层下端面处νk(y)和真实泊松比νr(y)相等,即

注意到随着子层个数N的增加,模型中Ek(y)和νk(y)将分别趋近于Er(y)和νr(y),这时模型达到准确表征界面层真实材料属性分布的目的。因此,该分层模型比单层界面层模型和互扩散模型更适合求解界面层材料属性在空间上任意变化时的裂纹问题。由于指数函数比线性函数和倒数更能使FGM裂纹问题的控制微分方程形式简单,且便于求解。因此,本文的分层模型比线性分层模型和倒数分层模型更便于公式推导和计算。此外,相对于均匀分层模型(子层中材料属性为常数),本文的分层模型能避免子层之间材料参数的不连续现象。
2 应力强度因子的求解
考虑平面应力状态下的弹性问题,在每一子层中,由物理方程、相容方程及式(2)可得到含Airy应力函数φk(k=1,2,…,N)的控制方程:

式中 ▽2为Laplace算子。
由于泊松比对应力强度因子影响很小[8],因此为了简化推导过程,可令:
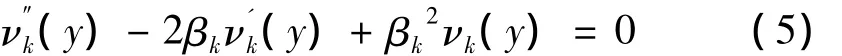
通过求解方程(5),可得到νk(y)具有以下函数形式:
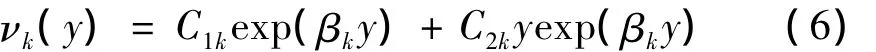
其中,未知量C1k和C2k可由式(3)确定。
对式(4)作关于坐标x,定义为=φkexp(-iax)dx的Fourier变换,并结合式(5),可得到:

方程(7)的通解为


对于界面层中每一子层,结合式(8)和模型中的几何方程,可得到Fourier变换域中位移和应力的向量表达式:

Tk的元素为
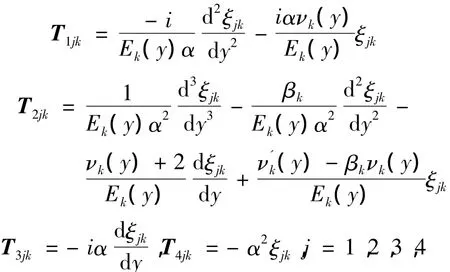
参照方程(4)可看出,衬层和推进剂中的Airy应力函数分别满足以下控制方程:

相应地,衬层和推进剂中位移和应力的向量表达式分别为

该模型的边界条件:
(1)衬层上端面处(y=h0+hL)x和y方向的位移均为0:

(2)各层界面处位移和应力的连续性条件:

式中 ΔSm={,,0,0}T;和为 Fourier变换域中裂纹面处位移增量;δmk为 Kronecker符号。
结合式(9)及式(11)~(13),并经过复杂的推导,可得到含裂纹的子层中位移应力向量Sm和ΔSm的关系式:
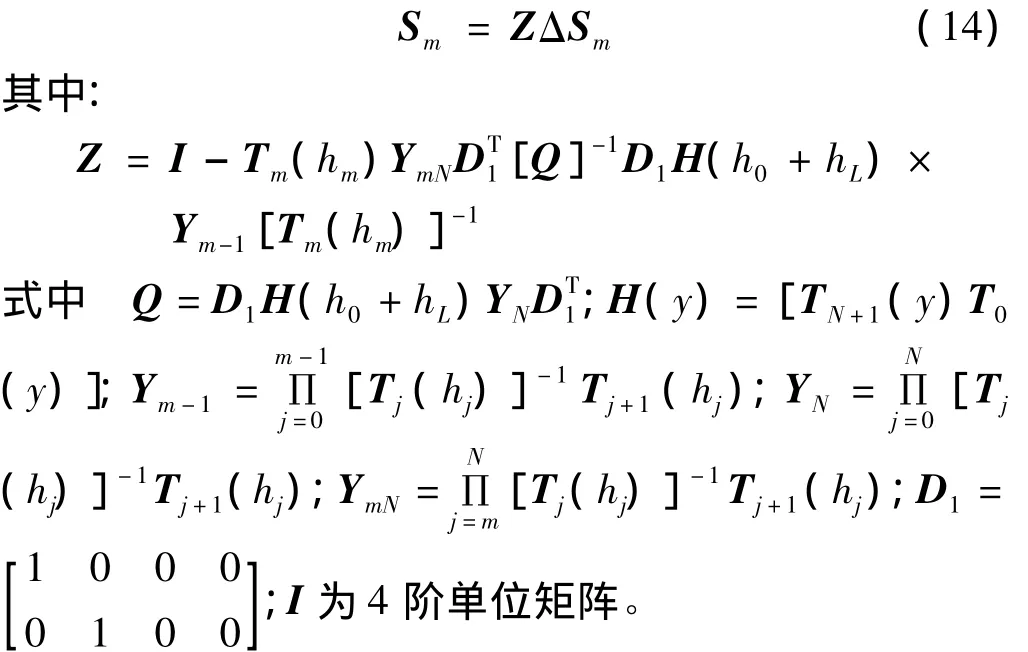

为了求解应力强度因子,引入以下2个位错密度函数:
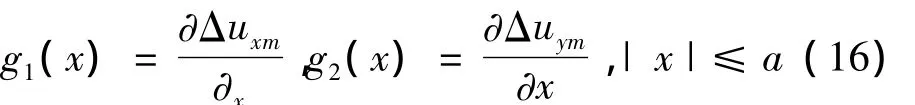
将式(16)代入式(15)并分离出应力分量后,可得到Cauchy型奇异积分方程组:


该问题的位移单值条件为

考虑到函数^g1(x)和^g2(x)在x=±1处的奇异性,这里将其分别表示为

结合式(17)~式(19),并根据 Erdogan等[16]提出的配点方法,可得到f1(x)和f2(x)的数值解,将其代入式(16)和式(19),可得到向量差ΔSm。根据各层材料位移应力向量的表达式(9)、(11)和(14)以及边界条件(13),并通过Fourier反变换,可直接得到衬层、推进剂和界面层各区域的应力场和位移场,而各处材料的应变场,可结合物理方程获得。本模型中,相对于衬层和推进剂,界面层中裂纹尖端处材料更容易发生破坏。因此,本文将重点分析应力强度因子(SIF)这一重要的断裂参量。
以裂纹右尖端为例,Ⅰ和Ⅱ型应力强度因子被p0=max})无量纲化后,可得到其对应的弹性解表达式:
由于模型中施加的是应力载荷,Ⅰ和Ⅱ型粘弹性应力强度因子可分别由对应的弹性应力强度因子和载荷函数相乘直接得到[17],与时间因子f0(t)无关。因此,本文只讨论应力强度因子对应的弹性解随各参数的变化规律。
3 算例验证与结果分析
3.1 算例验证
为了验证本模型的有效性,将其近似退化成单层界面层模型进行计算,并将结果和经典文献[8]对比。计算时,令裂纹位于界面层中线处,并在裂纹面上施加纯法向应力载荷,且hL相对于h0足够大。令Er(y)为指数型函数,E0/EN+1=3,ν0=νN+1=0.3。计算结果如表1所示。可见,本文模型和文献[8]的结果吻合良好,这可证明采用本文所建立的模型时计算结果正确可靠。
3.2 结果分析
文献[7]在实验中表明,推进剂/衬层界面贮存时间延长时,界面层的模量明显减小,而推进剂和衬层的模量相对变化不大。参照该实验数据,本文在计算时,选择衬层和推进剂的初始模量分别为3.3 MPa和3.9 MPa,其泊松比均为0.495,衬层和界面层厚度分别为1 mm和0.08 mm。将裂纹设置于界面层中线处,并设置子层个数N=6。
假设界面层中线处真实模量为Ep,从E0到Ep再到EN+1真实模量Er(y)随y坐标线性变化。另外,假设界面层真实泊松比函数νr(y)从ν0到νN+1也随y坐标线性变化。该模型中,通过调节Ep的值以体现界面层整体模量的变化。此外,基于文献[7]中界面层模量随贮存时间的变化规律,选取Ep为18、9、3 MPa,分别代表界面层贮存前期、中期和后期的模量。
综合图2、图3可看出,在纯法向和纯剪切应力加载下,界面层模量对KⅠ和KⅡ的大小及随裂纹长度的变化规律都有显著的影响。统一地讲,KⅠ和KⅡ的绝对值均随界面层贮存时间的延长(界面层模量的减小)而减小。当裂纹长度和界面层厚度相等时(c=0.08 mm),从界面贮存前期到后期,纯法向应力加载下的KⅠ和纯剪切应力加载下的KⅡ分别减小了52.2%和28.9%。因此,计算推进剂/衬层界面裂纹应力强度因子时,应充分考虑到界面层模量的影响,这也同时说明了建立本模型是非常必要的。
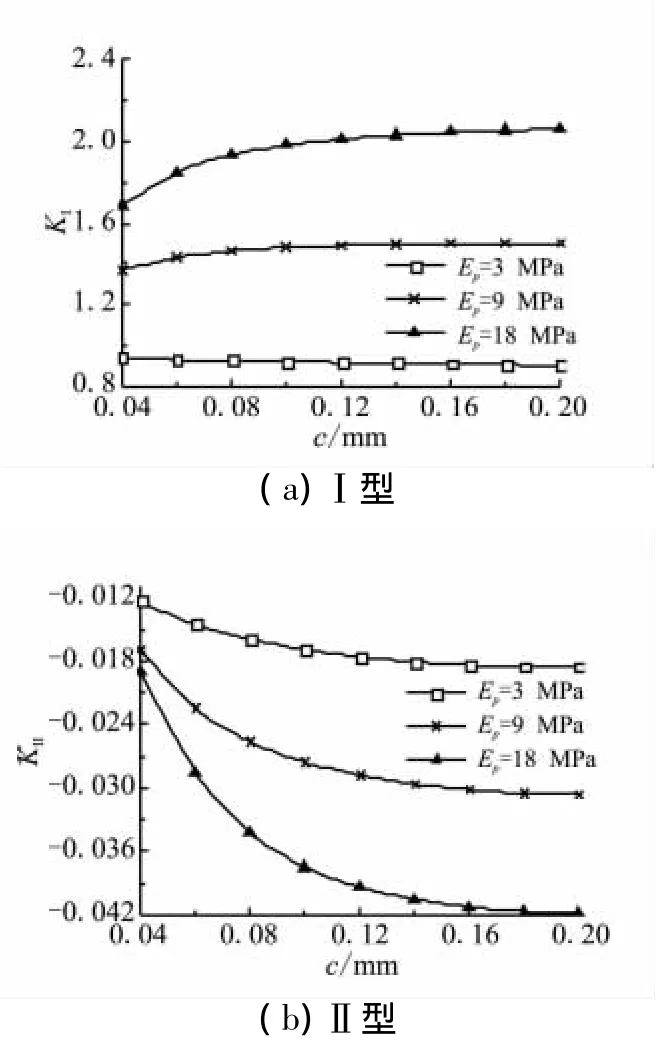
图2 法向应力加载下Ⅰ和Ⅱ型应力强度因子随裂纹长度的变化Fig.2 Variations of mode Ⅰ and modeⅡ stress intensity factors with crack sizes under normal stress loading
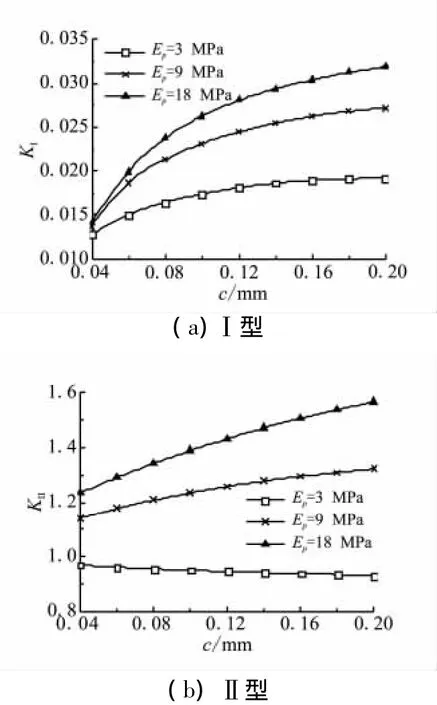
图3 剪切应力加载下Ⅰ和Ⅱ型应力强度因子随裂纹长度的变化Fig.3 Variations of modeⅠ andⅡstress intensity factors with crack sizes under shear stress loading
图4、图5分别显示不同贮存时期内,纯法向应力加载下的KⅠ和纯剪切应力加载下的KⅡ随界面层总厚度h0的变化规律(衬层厚度不变,c=0.1 mm)。在界面层贮存前期和中期,KⅠ和KⅡ均随着界面层厚度的增加而减小,而在贮存后期,KⅠ和KⅡ基本不随界面层厚度的变化而变化。总之,界面层厚度对KⅠ和KⅡ都有一定影响,但不如界面层模量的影响明显。

图4 法向应力加载下Ⅰ型应力强度因子随界面层厚度的变化Fig.4 Variations of mode Ⅰ stress intensity factors with interfacial zone's thicknesses under normal stress loading

图5 剪切应力加载下Ⅱ型应力强度因子随界面层厚度的变化Fig.5 Variations of mode Ⅱ stress intensity factors with interfacial zone's thicknesses under shear stress loading
4 结论
(1)文中为固体推进剂/衬层界面建立了一个新的指数型分层界面层模型,该模型通过将界面层划分成多个子层,可有效地求解界面层初始模量和泊松比在空间上任意变化时的裂纹问题。
(2)计算结果表明,界面层模量因界面贮存时间的延长而降低时,Ⅰ和Ⅱ型应力强度因子的绝对值显著减小。当裂纹长度和界面层厚度相等时,纯法向应力加载下的KⅠ和纯剪切应力加载下的KⅡ分别减小了52.2%和28.9%。此外,界面层厚度对Ⅰ和Ⅱ型应力强度因子的影响相对不明显。
(3)本文对功能梯度界面层模型在工程方面的应用有一定参考价值,对求解简单的推进剂/衬层界面断裂问题也有一定理论意义;而对于真实的三维固体推进剂/衬层粘结界面的断裂问题,也应充分考虑界面层有关参数对其影响,并可将本模型作适当扩展,再结合有限元等数值方法进行分析计算。
[1]蒙上阳,唐国金,雷勇军.固体发动机包覆层与推进剂界面脱粘裂纹稳定性分析[J].固体火箭技术,2004,27(1):46-49.
[2]许萌萌,胡春波,何国强.固体火箭发动机界面脱粘裂纹分析[J].固体火箭技术,2008,31(2):121-124.
[3]邢耀国,王立波,董可海,等.燃烧条件下影响推进剂脱粘面扩展的因素[J].推进技术,2001,22(1):77-80.
[4]Williams M L.The stresses around a fault or crack in dissimilar media[J].Bulletin of the Seismological Society of America,1959,49(2):199-204.
[5]Comninou M.The interface crack[J].Journal of Applied Mechanics,1977,44(4):631-636.
[6]Mak A F,Keer L M,Chen S H,et al.A no-slip interface crack[J].Journal of Applied Mechanics,1980,47:347-350.
[7]吴丰军,彭松,池旭辉.NEPE推进剂/衬层粘接界面层厚度表征方法研究[J].固体火箭技术,2008,31(6):650-652.
[8]Delale F,Erdogan F.On the mechanical modeling of the interfacial region in bonded half-planes[J].Journal of Applied Mechanics,1988,55(2):317-324.
[9]Wang X Y,Zou Z Z,Wang D.On the penny-shaped crack in a non-homogeneous interlayer under torsion[J].International Journal of Fracture,1996,82:335-343.
[10]Cheng Z Q,Zhong Z.Fracture analysis of a functionally graded interfacial zone between two dissimilar homogeneous materials[J].Science in China Series G:Physics,Mechanics & Astronomy,2006,49(5):540-552.
[11]Li Y D,Lee K Y.Mechanical modeling and transient antiplane fracture analysis for the graded inter-diffusion regions in a bonded structure[J].Meccanica,2009,44:389-408.
[12]Wang B L,Han J C,Du S Y.Cracks problem for non-homogeneous composite material subjected to dynamic loading[J].International Journal of Solids and Structures,2000,37:1251-1274.
[13]Wang Y S,Huang G Y,Gross D.On the mechanical modeling of functionally graded interfacial zone with a Griffith crack:plane deformation[J].International Journal of Fracture,2004,125:189-205.
[14]Cheng Z Q,Meguid S A,Zhong Z.Thermo-mechanical behavior of a viscoelastic FGMs coating containing an interface crack[J].International Journal of Fracture,2010,164:15-29.
[15]Paulino G H,Jin Z H.Correspondence principle in viscoelastic functionally graded materials[J].Journal of Applied Mechanics,2001,68(1):129-132.
[16]Erdogan F,Gupta G D.On the numerical solution of singular integral equations[J].Quarterly of Applied Mathematics,1972,29(4):525-534.
[17]Jin Z H.Some notes on the linear viscoelasticity of functionally graded materials[J].Mathematics and Mechanics of Solids,2006,11(11):216-224.
Exponential multi-layered interfacial zone model for solid propellant/liner interface crack
DI Ke,YANG Yue-cheng
(601 Staff Room,The Second Artillery Engineering University,Xi'an 710025,China)
An exponential multi-layered interfacial zone model was developed for the solid propellant/liner interface crack.In the model,the interfacial zone was divided into some sub-layers with the initial modulus of each sub-layer varying in an exponential manner.The method of Fourier transform was employed and a set of Cauchy singular integral equations was derived.A collocation method was used to obtain the semi-analytical solution of the crack problem under plane stress condition,and the influences of the interfacial zone's parameters on the stress intensity factors were discussed when the crack was subjected to normal and shear stresses.The results show that when the interfacial zone's modulus decreases,the absolute values of the stress intensity factors decrease significantly.The effects of the interfacial zone's thickness on the stress intensity factors are not significant relatively.
solid propellant;liner;interfacial zone;multi-layered model;crack;stress intensity factor
V512
A
1006-2793(2012)04-0516-06
2012-04-08;
2012-05-28。
邸克(1984—),男,博士生,研究方向为固体火箭发动机界面断裂。E-mail:12345aaaaak@163.com
(编辑:吕耀辉)
