单缝桥梁在温度作用下的结构受力计算

赵怡彬，邵旭东

(湖南大学，长沙 410082)

1 前言

桥台处伸缩缝是桥梁中易损且维护成本高的构件，为解决这一难题，国外常见的做法是采用整体式(半整体式)无缝桥梁，即通过桥头搭板将主梁与桥台的伸缩变形移至路桥接缝处，由路桥接缝吸纳所有变形。但路桥接缝容易受到土体不均匀沉降的影响，在汽车冲击荷载作用下，易变形破损［1，2］。

为了克服上述缺陷，笔者所在的课题组研发了全无缝桥梁。全无缝桥梁是针对跨径较小的桥梁，由连续桥面或连续桥梁结构、整体式桥台或半整体式桥台、跨过桥台与主梁连接的搭板以及连续配筋接线路面构成。这种全无缝桥梁通过主梁、搭板、接线路面协同工作，利用接线路面的有限变形和微裂缝来吸纳主梁的温度变形。取消伸缩缝，可以避免因伸缩缝装置而造成的桥头跳车、日常维护更换难等问题［3～6］。全无缝桥梁已经在广西、广东、河南、云南、宁夏等省(区)得到推广应用，运营性能良好，维护成本大幅降低。但一般仅用于桥长≤100 m的中小型桥梁。

为了将无缝化技术推广至大中型桥梁，文章在全无缝桥的基础上，提出了一种适用于长联桥梁的单缝桥梁，即只在原桥梁温度中心处设置1道伸缩缝。单缝桥取消了常规桥梁桥台处主梁与搭板间的伸缩缝，取消了国外整体式桥梁中搭板与路面之间的路桥伸缩缝。本文对这种新型单缝桥梁在温度作用下的受力性能进行了较为详细的研究。

2 单缝桥梁温度中心的计算

本文提出的单缝桥梁如图1所示，在原温度中心设置的伸缩缝可以释放主梁的大部分温度变形，在搭板末端和接线路面末端设置地梁，地梁与搭板或接线路面以预埋钢筋连接，保证二者在温度作用下可以协同受力和变形。接线路面通过变形和微裂缝来吸纳主梁的剩余变形，为使裂缝有规律地发展，接线路面按间距d(m)设置预锯缝。

2.1 计算简化模型1

在整体温度升高或降低时，主梁、搭板和接线路面均会发生伸长或缩短，但在整体结构中存在一个位置，这个位置在某一温差作用下位移为0，称为温度中心，温度中心两侧的水平力相等。温降时，单缝桥的受力如图2所示。

图1和图2中各参数的含义如下:L、Ls和Lp分别表示桥梁总长、搭板长度和接线路面长度;f11，f12，…，f1n分别为第1，2，…，n 号墩柱处支座对主梁的摩擦力，摩擦系数由支座的类型决定;μs、μp分别为搭板与垫层、接线路面与垫层的摩擦系数;K1、K2分别为搭板末端地梁和接线路面末端地梁处土体的刚度系数，由“m”法计算得到，假定K1、K2沿高度不发生变化。

图1 一种适用于长联桥梁的单缝桥梁图示Fig.1 The schematic diagram of single expansion joint bridge

图2 温降时计算模型1受力图示Fig.2 Force diagram of model 1 with temperature decreasing

如图3所示，以搭板的末端为x轴的原点，假设温度中心截面距搭板末端的距离为a，以温度中心为界，将结构分成左右两部分。图3中将搭板末端地梁以及接线路面末端地梁的土体水平作用力简化成刚度系数分别为K1、K2的弹性约束。不考虑摩擦力的弯矩作用，则主梁及搭板的摩擦力用∑F表示，∑ F= ∑ f1n+ γs·As·Ls·μs，其中 γs、As分别为搭板的重度和面积，nL和nR分别表示假定的温度中心左侧第1条裂缝和右侧最末1条裂缝所在的预锯缝编号。假定搭板末端的地梁发生Δ1的平移，其方向向右，接线路面末端的地梁发生Δ2的平移，其方向向左。

图3 以温度中心为界，温降时结构受力变形图示Fig.3 Force diagram of the both sides of temperature center

取温度中心左侧进行分析，如图4所示，温度中心左侧结构在水平力作用下可简化为1次超静定结构，在地梁处的土体弹性约束X1、各种摩擦力以及整体温降ΔT的作用下，搭板末端的地梁发生了Δ1的位移，Δ1的方向与X1方向相反。

建立力法方程如下:

图4 温度中心左侧受力图示Fig.4 Force diagram of the left side of temperature center

在温降作用下，接线路面的混凝土受拉，在事先形成的薄弱截面——预锯缝处可能开裂，接线路面通过裂缝吸纳主梁变形，因此各系数需考虑弹性变形和裂缝宽度。式(1)中δ11表示单位赘余力 作用在其本身的方向上所产生的位移，Δ1P表示在荷载∑F的作用下沿X1方向上产生的位移，Δ1t表示在温度荷载Δt的作用下沿X1的方向上产生的位移，δ11E和 Δ1PE分别表示系数的弹性部分，δ11S和 Δ1PS分别表示系数的塑性部分。假定左侧第1条裂缝出现的预锯缝编号是nL，则在［0，nLd)的范围内只需考虑弹性变形，而在［nLd，a］则需要考虑弹性变形和裂缝宽度。用下标i表示第i条预锯缝处裂缝的宽度(i为变量，在图4中未示出)。int(a)表示取整函数。根据各参数的几何意义得到具体表达式如下:

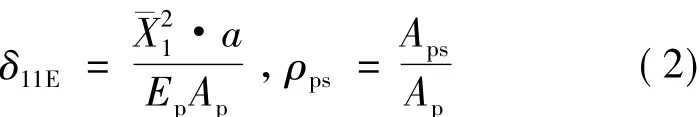
当1≤i＜nL时， W1Xi=0 (3)

当 nL≤i＜ int(a)时，

当1≤i＜nL时， W1Pi=0 (7)

当 nL≤i＜int(a)时，

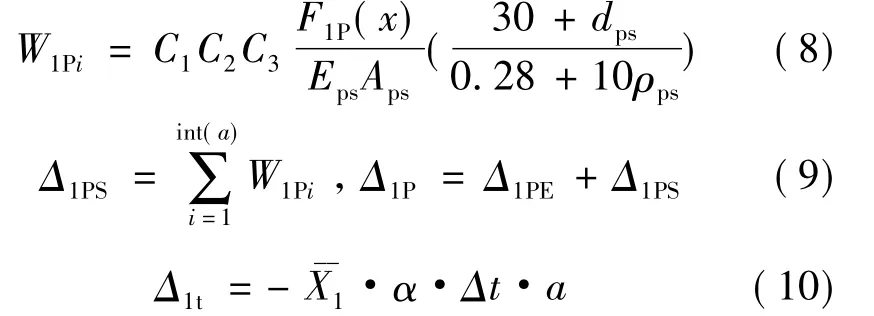
将式(13)～(21)代入式(12)，可以得到用a表示的X2，则温度中心右侧的水平力之和为

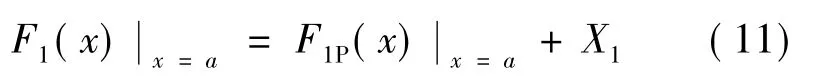
取温度中心右侧进行分析，如图5所示。同理，温度中心右侧结构在水平力作用下可简化为1次超静定结构，假设右侧最末1条裂缝出现的预锯缝编号为nR，则在(a，nRd］的范围内需考虑弹性变形和裂缝宽度，而在(nRd，Lp］只需考虑弹性变形。用下标j表示第j条预锯缝处裂缝的宽度(j为变量，未在图5中示出)。

图5 温度中心右侧受力图示Fig.5 Force diagram of the right side of temperature center

根据各参数的几何意义得到具体表达式:

当 int(a)≤j≤nR时，

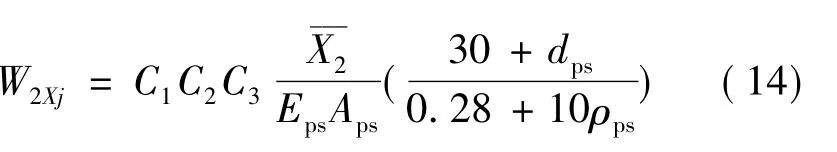
当 nR＜j≤n时，

当int(a)≤j≤nR时，

当 nR＜j≤n时，

将式(13)～(21)代入式(12)，可以得到用a表示的X2，则温度中心右侧的水平力之和F2(x)x=a为

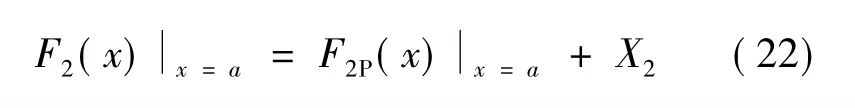
求出X1和X2后，接线路面任一位置x在温度作用下轴力F(x)及应力σ(x)为

根据单缝桥所在地区的最大温降值，可以求出原温度中心处主梁端部的变形量，根据变形量选择合理的伸缩缝型号，计算公式为

式(26)中，Δ、Δ1、Δe、Δse分别表示主梁端部变形、搭板末端地梁处位移、主梁的弹性变形及搭板的弹性变形。

2.2 计算流程

2.3 计算简化模型2

当温降作用较小时，混凝土受拉但仍处于弹性阶段，未开裂，此时分析方法与2.1节一致，但各系数均只需考虑弹性变形，δ11S和Δ1PE均为0。

2.4 计算简化模型3

当温降作用较大时，可在接线路面末端设置多道地梁(暂以2道为例)，地梁的间距为6 m，受力如图6所示。与前文类似，温度中心左侧简化为1次超静定结构，温度中心右侧简化为2次或多次超静定结构。

2.5 计算简化模型4

在温升作用下，结构受力如图7所示。混凝土的抗压强度约为抗拉强度的10倍，因此温升作用下不考虑混凝土开裂，各系数只需考虑弹性变形，方法与2.3 一致。

3 桥梁基本参数

一座14 m×20 m的空心板连续梁桥，伸缩缝设置于跨中，空心板梁高0.9 m，挖空直径为0.59 m，搭板长度Ls=8 m，高度为0.3 m，接线路面长度Lp=30 m，高度为0.24 m，搭板末端和接线路面末端各设1道地梁，地梁尺寸为0.6 m×1.2 m，如图8所示。搭板和接线路面均采用C30混凝土，预锯缝按间距1 m设置，浇筑时在预锯缝处填塞5 cm高，4 mm厚的小木板，形成薄弱面。接线路面按φ20@15配置，ρ=0.78%(ρ表示纵向受拉钢筋配筋率)，支座采用四氟滑板支座，支座与主梁底部的摩擦系数μ1=0.03［8］，垫层材料采用水稳定碎石，滑动摩擦系数 μs、μp由试验得到，μs= μp=1.8［9］，K1、K2根据地基规范［10］，取 K1=K2=5.0 × 104kN/m4，温降差ΔT=－20。C。以横向1 m宽的结构进行计算分析，计算结果如表1所示。

图6 温降时计算模型3受力图示Fig.6 Force diagram of model 3 with temperature decreasing

图7 温升时计算模型4受力图示Fig.7 Force diagram of model 4 with temperature decreasing

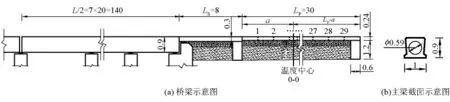
图8 实桥模型示意图(单位:m)Fig.8 Diagram of bridge model(unit:m)

表1 基本参数下的计算结果Table 1 Results of basic parameters

从表 1看出，温降 20℃作用下，σs=148 MPa＜HRB335抗拉强度设计值［σ］=280 MPa，Wmax=0.185 mm ＜［W］=1 mm，Δ2=2.216 mm ＜［Δ］=10 mm［11］，符合规范要求。主梁的最大附加应力为0.105 MPa，台后结构对主梁的影响很小，因此总长280 m的梁桥采用单缝桥结构是合理的，并且单缝桥主梁的最大附加应力只与主梁总长及支座摩擦系数有关。

4 结构参数分析

其他条件不变，分别改变如表2所示的某一个参数，用 CESEJB.for程序计算的结果在 4.1～4.8节分述。

表2 拟调整的参数Table 2 The parameters to be adjusted

4.1 不同支座类型的计算结果

其他参数不变，主梁改为板式橡胶支座μ1=0.3［8］的结果如表 3 所示。

表3 不同支座类型的计算结果Table 3 Results of different types of bearings

比较表1和表3可以发现，支座与主梁的摩擦系数增大，∑F增大，温度中心向桥台方向靠近。采用四氟滑板支座时接线路面的Nmax为273 kN，采用板式橡胶支座时Nmax为531 kN，后者比前者增大了95%，同时WT从2.905 mm增加至7.4 mm，增加了155%，主梁最大附加应力从0.105 MPa增加至1.05 MPa，增大了9倍，对这种新型结构的受力不利。因此应在考虑抗震要求的基础上尽量选用摩擦系数较小的支座，让主梁可以较自由地纵向滑动。在实桥设计中，应避免出现温度中心位于搭板的现象。

4.2 不同配筋率的计算结果

其他参数不变的情况下，接线路面采用不同的配筋方式(φ20@15、φ16@15、φ20@20、φ16@20)，计算结果如表4所示。

表4 不同配筋率的计算结果Table 4 Results of different reinforcement ratios

从表4可以看出，配筋面积As越小，Nmax越小，钢筋应力σs越大，裂缝宽度Wmax越大，Δ2越小。以配置 φ 16@20的钢筋为例，Wmax=0.31 mm，σs=261 MPa＜［σ］=280 MPa，均能满足规范要求。因此在满足规范的前提下，可适当减小配筋率。

4.3 不同接线路面长度计算结果

其他参数不变，改变接线路面的长度(Lp=15 m、20 m、25 m、30 m、35 m、40 m)，计算结果如图9所示。

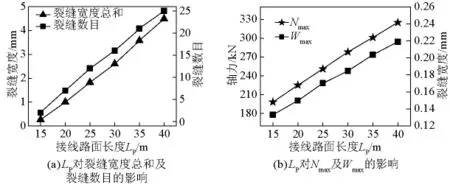
图9 不同接线路面长度的计算结果Fig.9 Results of different pavement length

从图9可以看出，接线路面长度Lp从15 m增加至40 m，裂缝数目增加，裂缝宽度总和增加，Nmax增大，Wmax也随之增大。Lp=15 m时，Nmax=198 kN，Lp=40 m 时，Nmax=325 kN，增加了64%。接线路面长度增加反而不利于结构受力，因此从经济性和安全性的角度考虑，接线路面不宜过长，但从结构整体刚度渐变的角度，接线路面的长度不宜太短，推荐采用30 m的接线路面。

4.4 不同滑动摩擦系数计算结果

其他参数不变，改变接线路面与垫层的滑动摩擦系数(μp=1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9、2.0)，计算结果如图 10 所示。

图10 不同摩擦系数的计算结果Fig.10 Results of different friction coefficients

从图10中可以看出，滑动摩擦系数μp增大，裂缝数目增加，Nmax增大，Wmax随之增大。滑动摩擦系数越大，接线路面受力越不利。因此建议在施工中，在垫层与接线路面之间铺设土工格栅，既能起到加筋的作用，又可以减少摩擦;或选择较光滑的河卵石作为垫层材料，尽量避免多棱角粗糙的山石，以减小摩擦系数。

4.5 不同土体刚度计算结果

其他参数不变，改变地梁埋置处的土体类型和土体的刚度系数(K=0.5×107～8×107)，以模拟不同类型的回填土及压实程度，计算结果如图11和表5所示。

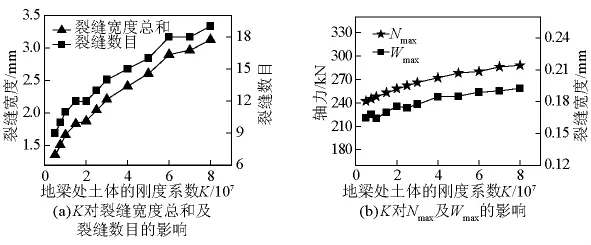
图11 土体不同刚度系数的计算结果Fig.11 Results of different soil stiffness

表5 土体不同刚度对赘余力 及地梁位移Δ2的影响Table 5 Force and displacement results of different soil stiffness

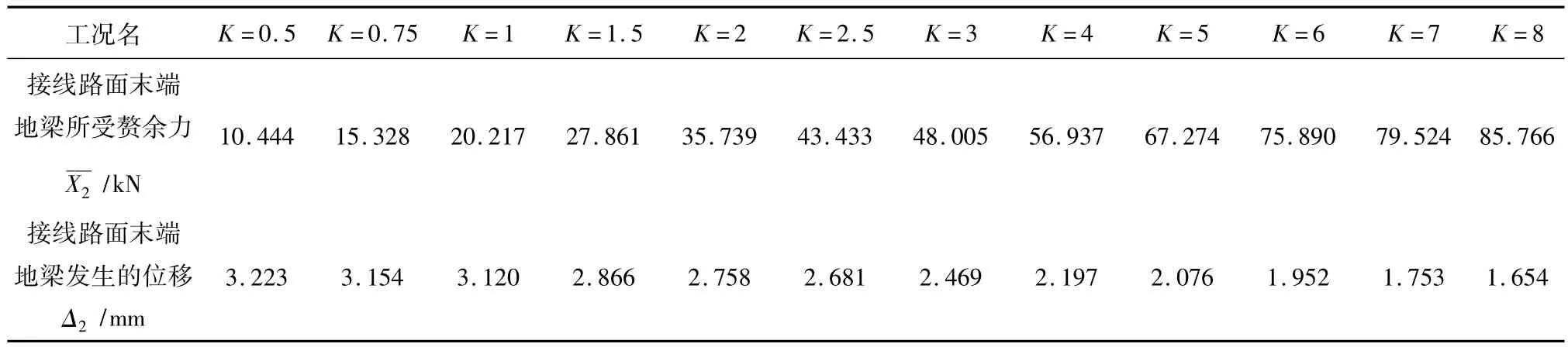
表5 土体不同刚度对赘余力 及地梁位移Δ2的影响Table 5 Force and displacement results of different soil stiffness

注:K值表示地梁处土体的刚度系数，系数为107

工况名 K=0.5 K=0.75 K=1 K=1.5 K=2 K=2.5 K=3 K=4 K=5 K=6 K=7 K=8接线路面末端地梁所受赘余力X2___/kN 10.444 15.328 20.217 27.861 35.739 43.433 48.005 56.937 67.274 75.890 79.524 85.766接线路面末端地梁发生的位移Δ2/mm 3.223 3.154 3.120 2.866 2.758 2.681 2.469 2.197 2.076 1.952 1.753 1.654

从图11中可以看出，K从0.5×107增加至8×107，即从可塑性粘土、硬塑性粘土、粗砂到砾石，裂缝数目、裂缝宽度以及最大轴力Nmax、Wmax均增大，即地梁近似于锚固在岩石里时，反而不利于地梁受力。综合图11和表5可看出，地梁处土体刚度K增大，接线路面的Nmax增大，但Δ2减小。因此不能选用K值过大的土层，不利于接线路面受力，但也不能选用K值太小的土层，以免地梁位移过大，推荐采用土体刚度系数为K=2.5×107～7×107的回填土。在全无缝桥中，如果土的可压缩性较大，即K值较小，地梁处会发生过大位移而使接线路面整体被拖动，导致结构失效，因此地梁处的土一定要紧密压实［12］，对施工的要求比较严苛，而新型的单缝桥梁对土体的适应性较强，施工要求可以适当放松。

4.6 不同桥梁长度计算结果

其他参数不变，改变单侧桥梁的长度(L/2=20 m、40 m、60 m、80 m、100 m、120 m、140 m、160 m)，计算结果如图12所示。

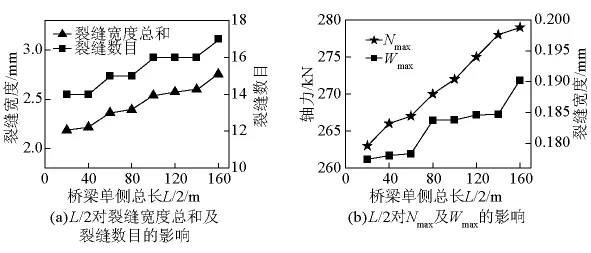
图12 不同桥梁长度的计算结果Fig.12 Results of different total length of bridge

从图12中可以看出，L/2从20 m增大到160 m，裂缝数目由14条增加至17条，仅新增3条;接线路面的裂缝宽度总和由2.186 mm增加至2.755 mm，仅增加了26%，桥长增加对结构性能的影响不大，设置在原桥梁温度中心处的伸缩缝的确能极大地释放桥梁的温度变形。L/2=160 m时，Wmax=0.190 mm ＜［W］=1 mm，Nmax=279 kN，σs=147 MPa＜［σ］=280 MPa。因此这种单缝桥梁对于总长300 m左右的梁桥是适用的。

4.7 不同温降值计算结果

其他参数不变，改变温降值(ΔT=－5℃、－10℃、－15℃、－20℃、－25℃、－30℃、－35℃、－40℃)，计算结果如图13所示。

从图13中可以看出，裂缝数目由－5℃时的9条增加至－40℃时的25条，增加得较多，但即使在－40 ℃的温度下，Wmax=0.25 mm，远小于文献［11］所容许的1 mm，此时 Nmax=337 kN，σs=180 MPa，小于HRB335抗拉强度设计值，因此这种新型的结构可以用于温差较大的地区，极大地拓宽了无缝化技术的使用范围。

图13 不同温降值的计算结果Fig.13 Results of different temperatures

4.8 温升作用下的最大应力

用CESEJB.for计算当ΔT=20℃时的各种工况，并计算模型在 ΔT分别为5℃、10℃、15℃ 、20℃、25℃、30℃、35℃、40℃的受力情况。仅选取最不利的工况用图表加以阐述:当温升ΔT=20℃时，Lp变化对结构的影响如图14所示，ΔT分别为5℃、10℃、15℃ 、20℃ 、25℃、30℃、35℃、40℃的结构受力如图15所示。

图14 不同接线路面长度温升时的计算结果Fig.14 Results of different pavement length with temperature increasing

从图14可以看出，在温升ΔT=20℃作用下，随着接线路面长度Lp增大，接线路面Nmax增加，这与温降作用的规律一致，并且Lp=40 m时，Nmax=392 kN，预锯缝处接线路面混凝土的应力 σc=392 kN/0.14 m2=2.8 MPa，小于 C30 混凝土的抗压强度(fcd=13.8 MPa)，混凝土不会开裂。

比较图9和图14可以看出，在其他参数相同，Lp=40 m时，温升作用下，接线路面不开裂，Nmax=392 kN，而温降作用下，接线路面共25条微裂缝，Nmax=325 kN，比温升作用时减小了17%。这说明，接线路面通过微裂缝吸纳了主梁的部分变形，释放了部分约束，减少了结构内力。

从图15可以看出，随着温升值的增大，接线路面的最大轴力Nmax增大，这与在温降值增大时的规律一致，ΔT=40℃时，接线路面中Nmax=408 kN，接线路面混凝土的应力 σc=408 kN/0.14 m2=2.91 MPa ＜13.8 MPa，混凝土不开裂。因此这种新型单缝桥梁对温度的适应性较强。比较图13和图15，可以得到与上文一样的结论。

5 结语

1)温降较大时，混凝土受拉，预锯缝所形成的薄弱处会开裂，以吸纳梁体的部分水平位移，但各裂缝宽度远小于规范所规定的最大裂缝宽度;温升时，混凝土受压，不开裂。温降作用是结构的较不利状况。

2)增加配筋率，会增加结构内力，但能有效减小裂缝宽度;接线路面越长，接线路面的最大轴力越大，推荐采用30 m左右的接线路面;尽量减小接线路面与垫层之间的摩擦系数，在施工中，垫层上应铺设土工格栅、采用较光滑的卵石，可减少摩擦系数，其中土工格栅还可以起到加筋和防止反射裂缝的作用。

3)单缝桥适用于温差较大的地区，并且适用于总长300 m以内的梁桥。

［1］Arockiasamy M，Butrieng N，Sivakumar M.State of the art of integral abutment bridge:design and practice［J］.Journal of Bridge Engineering，2004，9(5):497 －506.

［2］White H Ⅱ，Petursson H，Collin P.Intergral abutment bridges:the European way［J］.Practice Periodical on Structural Design and Construction，2010，15(3):201 －207.

［3］Jin Xiaoqin，Shao Xudong，Yan Banfu，et al.New technologies in China’s first jointless integral-abutment bridge［C］.IABSE Symposium on Metropolitan Habitats and Intrastructure.Shanghai，2004.

［4］Jin Xiaoqin，Shao Xudong，Peng Wanghu，et al.A new category of semi-integral abutment in China［J］.Structural Engineering Intemational，2005，15(3):186 － 188.

［5］邵旭东，占雪芳，金晓勤.带地梁的新型无缝桥基本性能研究［J］.中国公路学报，2010，23(1):43－48.

［6］金晓勤，邵旭东.半整体式全无缝桥梁研究［J］.土木工程学报，2009，42(9):68－73.

［7］JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京:人民交通出版社，2004.

［8］JT/T 4—2004公路桥梁板式橡胶支座［S］.北京:电子工业出版社，2004.

［9］邵旭东，陈志新，金晓勤.无缝桥加筋接线路面的拉伸变形性能［J］.中国公路学报，2010，23(6):34－40.

［10］JTG D63—2007公路桥涵地基与基础设计规范［S］.北京:人民交通出版社，2007.

［11］JTG D40—2002公路水泥混凝土路面设计规范［S］.北京:人民交通出版社，2003.

［12］金晓勤.新型全无缝桥梁体系设计与实验研究［D］.长沙:湖南大学，2007:1－50.