两类6 维幂零李代数的上同调群

杨恒云，叶鑫

(上海海事大学 文理学院，上海 201306)

0 引言

幂零李代数是一类重要的李代数.［1-2］设L是复数域C 上的李代数.{Lk}(k≥0)是L 的降中心序列.若存在k∈N，使得Lk={0}，则称L为幂零李代数.由于幂零李代数中更特殊的低维幂零李代数的分类问题尚未解决，许多学者一直以来都致力于对低维幂零李代数结构的研究，其中包括对导子代数、自同构群、二上循环等的研究.例如:文献［3］研究一些特殊的10 维幂零李代数的导子代数;文献［4］研究小于等于4 维复幂零李代数的导子代数;2005年，de GRAAF［5］利用SCHNEIDER［6］给出的小于等于6 维幂零李代数的分类，得到特征不为2 时小于等于6 维幂零李代数的所有表达式.

本文研究文献［5］中给出的两类6 维复幂零李代数的低阶上同调群.记这两类复幂零李代数为L1和L2，设他们的基均为{x1，x2，…，x6}，李括号积分别为

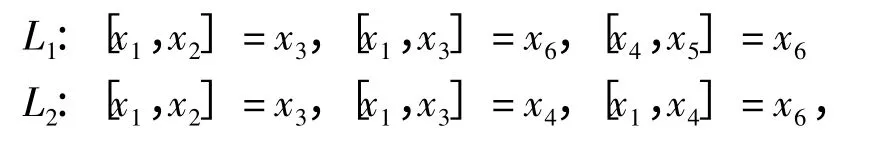
其余李括号积全为零.本文刻画出这两类李代数的导子代数、自同构群和二上循环.

1 导子代数

研究L1和L2的导子代数结构，给出它们的所有内导子和外导子.

首先给出一些基本定义.

定义1 设L是复数域C 上的李代数，D是L上的一个线性变换，且满足

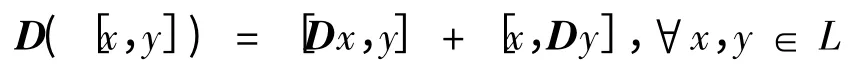
则称D为L 的导子.记L 的所有导子的集合为Der(L).

显然，Der(L)是一般线性李代数gl(L)的子代数，称其为L 的导子代数.令ad L={ad x|x∈L}，则ad L是Der(L)的理想，称其为L 的内导子代数.

定理1 李代数L1的导子代数为

式中:di(i=1，2，…，9)是L1的外导子，且满足条件(d1(x1)=x1，d1(x3)=x3，d1(x5)=2x5，d1(x6)=2x6;d2(x1)=x2;d3(x1)=x4，d3(x5)=-x3;d4(x1)=x5，d4(x4)=x3;d5(x2)=x2，d5(x3)=x3，d5(x5)=x5，d5(x6)=x6;d6(x2)=x6;d7(x4)=x4，d7(x5)=-x5;d8(x4)=x5;d9(x5)=x4)，di(i=1，2，…，9)在其他生成元上的作用为零.

证明 任取D∈Der(L1)，设

将D 作用在［x1，x2］=x3的两边，得

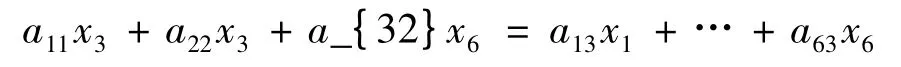
所以有

将D 分别作用在［x1，x3］=x6，［x4，x5］=x6的两边，得

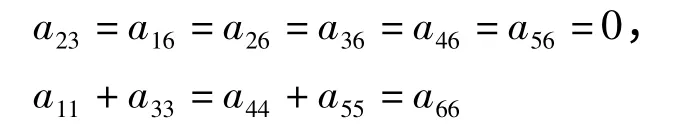
将D 作用在L1的其他所有的李括号积上，得

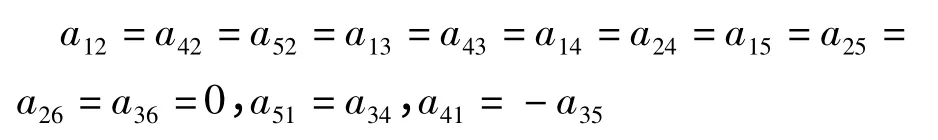
从而有

利用L1的定义，易得D-a32ad x1+ a31ad x2+a61ad x3-a65ad x4+a64ad x5对应的矩阵为

定理得证.

定理2 李代数L2的导子代数为

式中:di(i=1，2，…，6)是L2的外导子，且满足条件(d1(x1)=x1，d1(x2)=2x2，d1(x3)=3x3，d1(x4)=4x4，d1(x5)=3x5，d1(x6)=5x6;d2(x1)=x2，d2(x4)=x6，d2(x5)=-x4;d3(x1)=x5，d3(x3)=-x6;d4(x2)=x4，d4(x3)=x6;d5(x2)=x5;d6(x5)=x6)，di(i=1，2，…，6)在其他生成元上的作用为零.

证明 任取D∈Der(L2)，设

将D 作用在L2的所有李括号积上，经过整理计算得到D 所对应的矩阵为

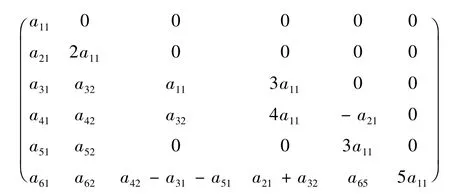
定理得证.

2 自同构群

定义2 设L是复数域C 上的李代数，若L 的可逆线性变换σ 满足

则称，σ是L 的自同构.

显然，L 上的自同构关系是一个等价关系.L 的所有自同构构成一个群，称其为L 的自同构群，记作Aut L.

定理3 李代数L1的自同构群Aut L1={D1∈M at(6，C)}，D1的表达式见证明过程.

证明 任取σ∈Aut L1，设

由［σ(x1)，σ(x2)］=σ(x3)得

将σ 分别作用在［x1，x3］=x6，［x4，x5］=x6的两边，利用上面的结果得

由［σ(xi)，σ(x3)］=0，i=2，4，5，得

由于σ是自同构的，有a66≠0，从而a11和a33≠0，所以

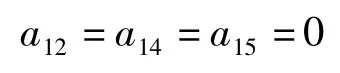
将σ 分别作用在［x1，x4］=0，［x1，x5］=0 的两边，得

由于a11≠0，得

将σ 分别作用在［x2，x4］=0，［x2，x5］=0 的两边，得

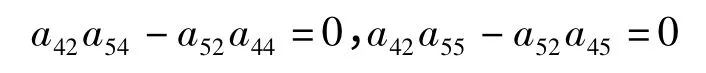
若a42≠0，则必有a52≠0，否则与a66≠0 矛盾.在这种情况下，由上面两个式子可以得

这与a66≠0 矛盾，所以

将以上结果整理后有

从而σ 所对应的矩阵为

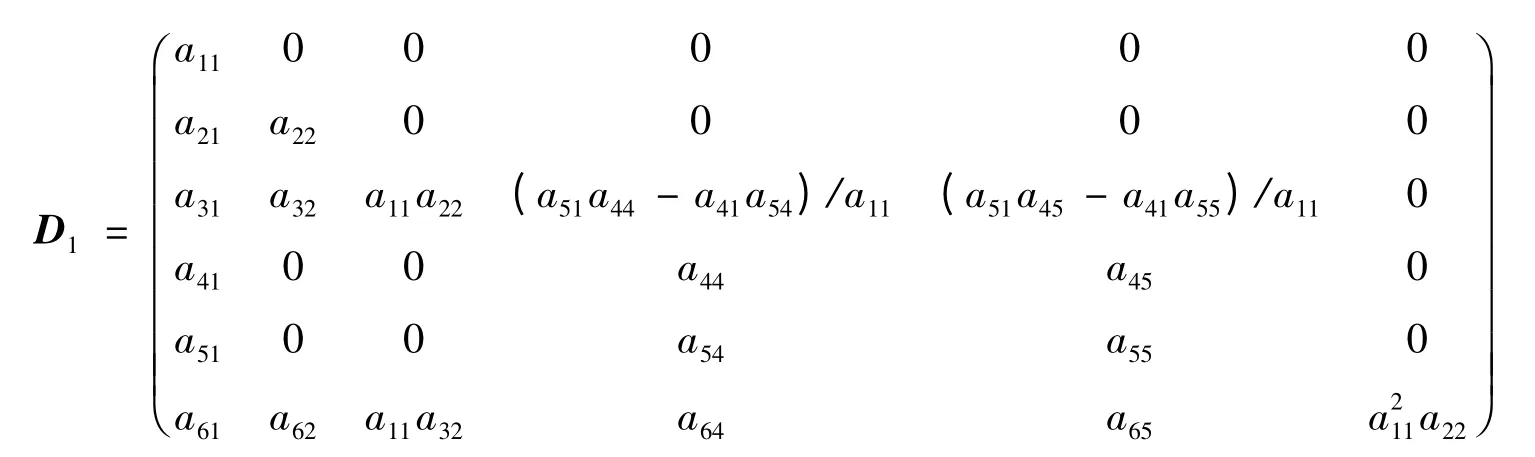
其中a44a55-a54a45=a66≠0，a11，a22和a33≠0.定理得证.

定理4 李代数L2的自同构群Aut L2={D2∈M at(6，C}，D2的表达式见证明过程.

证明 任取σ∈Aut L2，设

类似定理3 的证明方法，得到σ 所对应的矩阵为

其中a11≠0.定理得证.

3 二上循环

定义3 设L是复数域C 上的李代数，L 上的双线性函数θ:L×L→C 满足

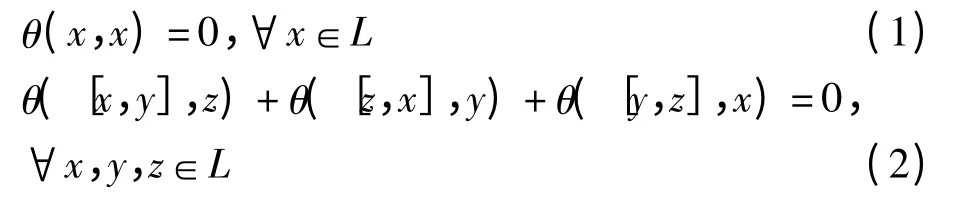
则称θ为L 的二上循环.L 的所有二上循环组成的集合记为Z2(L，C).

设V是C 上的一维线性空间，0≠c∈V.在线性空间Lθ=L⊕V 上定义

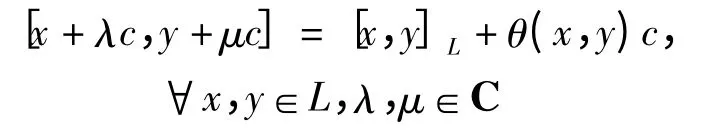
则Lθ是L 的中心扩张.由此看到，二上循环在李代数的中心扩张中起着重要作用.对L 上的任一线性函数f:L→C，令

则θf是L 的一个二上循环，称为二上边缘或平凡二上循环.L 的所有二上边缘张成的向量空间记为B2(L，C).设η∈B2(L，C)，则Lθ≌Lθ+η.因此，只需考虑下面的集合

称为L 的二上同调群.

下面给出李代数L1和L2的二上同调群.

定理5 dim H2(L1，C)=6.

证明 任取θ'∈Z2(L1，C)，定义L1上的一个线性函数f:L1→C 如下

令θ=θ'-θf，则有

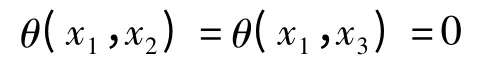
将x1，x2，x3代入条件(2)得

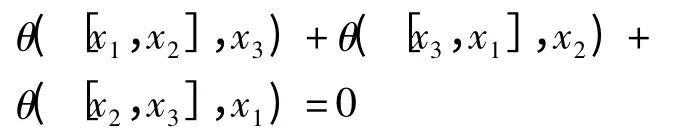
从而

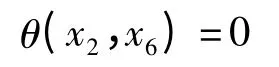
在条件(2)中取遍L1的一组基后，结合条件(1)，得

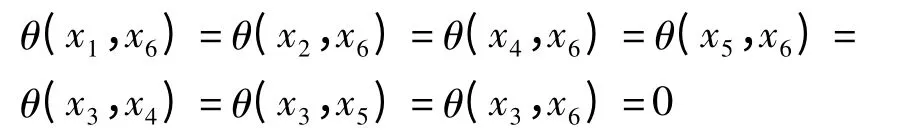
并且θ(x1，x4)，θ(x1，x5)，θ(x2，x3)，θ(x2，x5)，θ(x4，x5)是自由的.定理得证.

定理6 dim H2(L2，C)=5.

证明 任取θ'∈Z2(L2，C)，定义L2上的一个线性函数f:L2→C 如下

令θ=θ'-θf，则有

利用公式(2)和L2的定义，经过计算得到仅有θ(x1，x5)，θ (x2，x3)，θ (x2，x5)，θ (x2，x6)=θ(x3，x4)，θ(x1，x6)=θ(x2，x4)=θ(x3，x5)是自由的.定理得证.

［1］孟道骥.复半单李代数引论［M］.北京:北京大学出版社，1998:38-44.

［2］HUMPHREYS J E.Introduction to Lie algebras and representation theory［M］.Springer，1972:11-20.

［3］杨恒云，林磊，方燕.10 维线状李代数［J］.青岛大学学报，2009，22(2):34-40.

［4］范素军，周檬，崔丽娟.幂零李代数的导子代数的结构［J］.河北师范大学学报，2009，33(5):1-3.

［5］de GRAAF W A.Classification of 6-dimensional nilpotent Lie algebras over fields of characteristic not 2［J］.J Algebra，2007，309(2):640-653.

［6］SCHNEIDER C.A computer-based approach to the classification of nilpotent Lie algebras［J］.Experiment Math，2005，14(2):153-160.