三相光伏并网逆变器控制策略

刘 波 杨 旭 孔繁麟 叶海忠 于 虹

（1.西安交通大学电气工程学院 西安 710049 2.广东明阳龙源电力电子有限公司 中山 528400）

1 引言

随着现代化日益增长的能源需求，新能源技术如光伏发电和风力发电等正在经历着一场全面深刻地发展成熟，逆变并网技术及其对电网质量的影响正得到人们更多地关注。影响电网质量的一个主要因素就是电流谐波含量。CNCA-CTS004《并网光伏发电专用逆变器技术要求和试验方法》中规定逆变器满负载运行时，电流总谐波畸变率限值为5%，奇次谐波中3～9次小于4%，11～15次小于2%，35次以上小于0.3%。

针对如此严格的谐波要求，在电压源 PWM 逆变器应用中，LCL滤波器取代了传统的L 滤波器，其在减小了体积的同时对电流高频分量具有更好的滤波效果[1]，但是 LCL 三阶系统的引入，增加了二阶谐振零极点，其谐振极点的零阻抗特性带来的可能的振荡[2]，对系统电流环控制提出了更大的挑战。

在传统三相逆变控制中，PI控制器由于无法实现交流信号的无静差跟踪，稳态电流存在较大的误差，而引入电网电压前馈的PI控制增强了系统的动态性，但是由于其积分功能对交流信号天然的缺陷，依旧不能有效的减小稳态误差[3]。

为减小稳态静差，dq旋转坐标下的PI控制对三相逆变系统具有天然的优势，其将交流转换为直流后发挥了积分控制的作用，可以实现无静差控制。与此同时，比例谐振（PR）控制也开始广泛应用，PR控制虽然在谐振频率上具有无穷大增益，从理论上可以实现基波电流的无静差控制[4]，但实际应用中由于电网频率存在波动，以及模拟或数字离散化实现时存在精度限制，一旦基波频率和PR谐振频率不一致，该处PR的增益会非常小，将使控制失效[5]。因此文献[6]改进采用了准谐振PR控制，该方法增加了可调的选频宽度，但在谐振频率点上增益有限，因此无法从理论上实现基波跟踪的无静差。

为此，本文提出了一种基于dq旋转坐标系下的PI级联准谐振PR控制器设计方案，与传统方法相比该方法在旋转坐标下通过PI实现了基波的稳态无静差控制，通过PR实现了对特定谐波的充分抑制，此外在旋转坐标下引入了电网电压前馈，增加了系统对电网的抗扰能力，实现了并网起动电流无冲击。同时三相系统在dq下的控制，可以实现有功无功的自主调控。

本文首先分析了光伏并网逆变系统的结构和模型，在此基础上分析讨论了控制方法，给出了控制器的实现步骤，最后通过仿真及在一台实际100kW光伏阵列并网逆变系统中对比实验，表明了控制算法的有效性。

2 系统结构模型

2.1 系统结构

本文所用光伏并网逆变器拓扑，直流侧为100kW光伏阵列，逆变侧采用IGBT三相全桥电路，逆变输出电流经过LCL滤除高次谐波后，经工频变压器隔离升压后并网发电。系统控制算法采用了TI公司的浮点型DSP 28335实现，在DSP内进行数字软锁相，实现和电网频率及相位的同步[7,8]，之后根据MPPT指令控制逆变电流，以软起动纯有功方式实现光伏逆变器的无冲击并网。

2.2 系统模型

为提高直流利用率，减少开关次数[9]，采用了SVPWM 调制，三相逆变器电路模型如图1 所示。

图1 三相逆变器模型Fig.1 Model of the three phase inverter

图中，Lf为逆变侧电感，Lg为网侧电感，C为滤波电容，Rf、Rg、Rc分别为各自的ESR，ik和分别为三相逆变电流和并网电流。可知系统在三相静止坐标系下的电路方程如下：

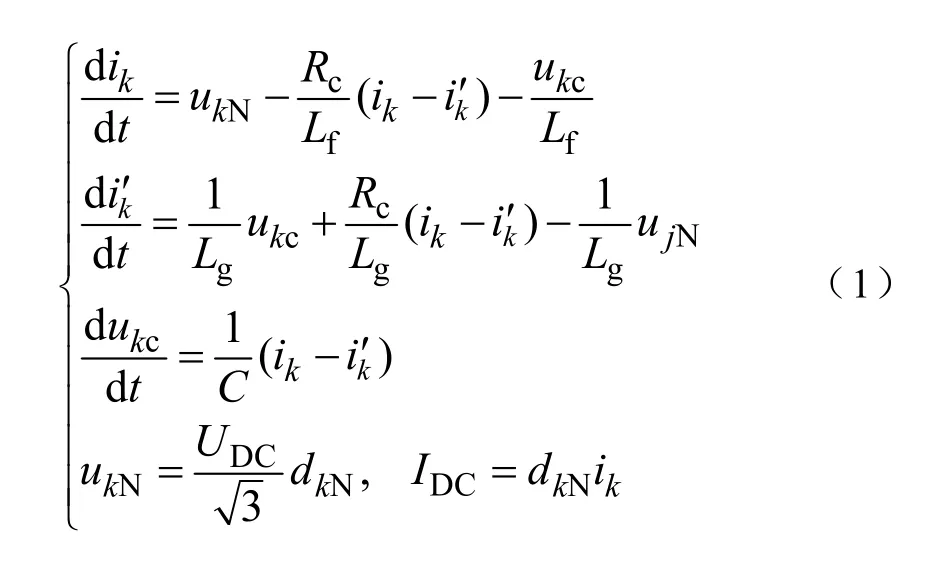
式中，k=a，b，c；j=A，B，C。

在三相对称电网下，可以得到旋转坐标系 dq下的电路方程，见式（2），其dq 下模型如图2 所示。

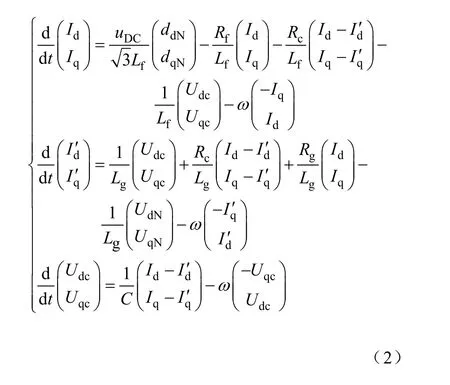
图2 dq 坐标下系统平均模型Fig.2 The average model of system under dq rotate frame

对于耦合电压源LfIq、LfId，容易实现解耦，而耦合电流源CfUqc、CfUdc，由于控制量不直接产生作用，难以解耦[10]，在分析中考虑到q 上分量较小，为简化设计而忽略，同时假定电网三相平衡，忽略直流电压波动，从而将非线性耦合系统转化为线性系统，因此可直接以此大信号模型设计控制器。

3 控制器实现

采用LCL 滤波器，引入了谐振环节，如果以网侧电感电流作为反馈，则控制对象为三阶系统，相频特性曲线衰减很快，为留有充裕相位余量，则系统增益和带宽将受到很大限制，控制效果不好，文献中提到了其他方法[11-13]，可以改造控制对象，但在三相系统中传感器成倍增加，采用多环控制结构，使得设计和控制都颇显复杂。本文采用逆变器侧电感电流反馈，控制对象高频段为一阶系统，采用单电流环控制，就可以保证系统的稳定性，降低了控制难度。但必须注意，并网电流并不完全取决有逆变电感电流的调控，还取决于电网电压和LCL 滤波器的参数，由于存在LCL 谐振峰，以及电网谐波的影响，网侧电流可能存在相应的谐波分量，通过在dq 旋转同步坐标系下，电网电压的前馈抵消，同时引入PR 控制器进行特定频率谐波消去，可以达到较好的并网逆变效果。

先忽略耦合项，则dq 轴下，根据叠加原理，逆变电流受直流电压和网侧电压共同决定

式中，x=d、q；Gix_dx(s)是逆变电流对占空比的传 递函数，是受控对象

Gix_uxN(s)是逆变电流对电网电压的传递函数，是扰动项

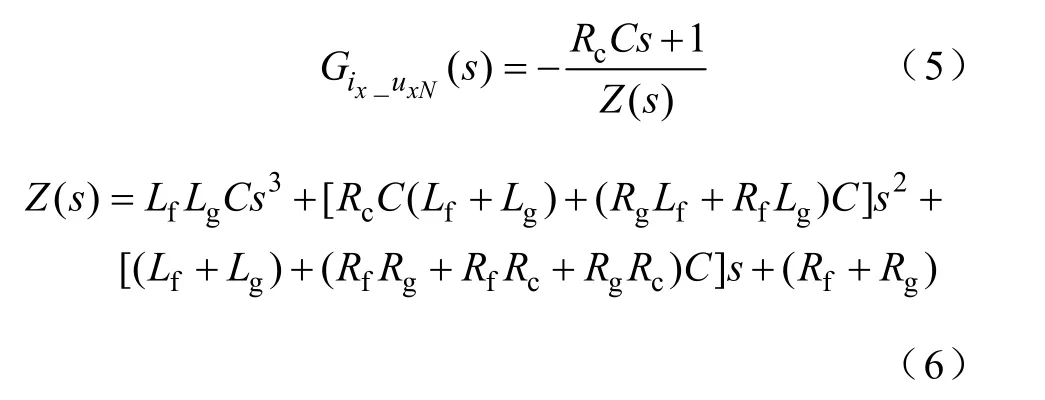
令

由此得

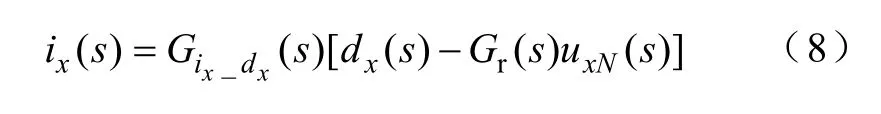
结合式（3）～式（8），可知系统经过解耦和网侧电压前馈后的控制框图如图3 所示，其中GC(s)为待定控制器。

图3 系统控制框图Fig.3 Control block of system

在旋转dq 坐标下三相交流电流转化为直流量后，id、iq分别对应了有功和无功电流，具有相同的电路模型，所以控制器的设计是一样的，由式（4）、式（6）可知，受控对象的伯德图如图4 所示，采用PI 控制器就可实现对基波电流的无静差跟踪

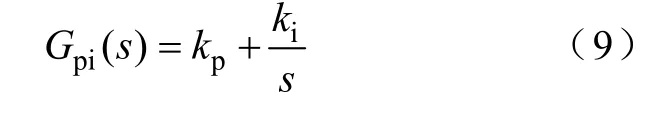
由于光伏MPPT 电压随光照在450～800V 之间变化，设计中取最恶劣情况UDC=800V。在实例中，kp=0.003 7，ki=0.513 9。

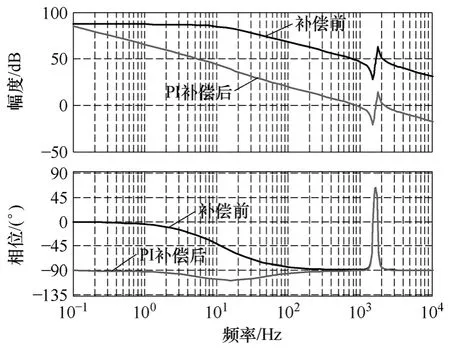
图4 使用PI 控制器补偿前后的开环传递函数伯德图Fig.4 Bode diagram of open loop transfer function before and after compensation by using PI controller

从图4 补偿后的伯德图上可以看到，采用逆变侧电感电流反馈控制，简化了控制环设计，但是由于LCL 谐振峰的存在，在f=2kHz 处，存在二次穿越，在该处比较靠近开关频率，数字控制延时较大，实际的相位余量将比伯德图上减小不少，可能影响系统的稳定性，如果要把谐振峰压下去，则要将环路增益减小，系统带宽将降低，这样系统动态性能降低，而且对低次谐波的抑制能力将减弱，所以只能在保证系统足够相位余量的稳定的情况下，在带宽和增益之间权衡。这样，为补偿控制环对电网谐波的抑制能力，在dq 系下加入电网电压前馈，如图3所示，可以抑制电网侧谐波扰动和提高系统动态响应能力。前馈因子Gr(s)由式（7）可得，伯德图如图5 所示。

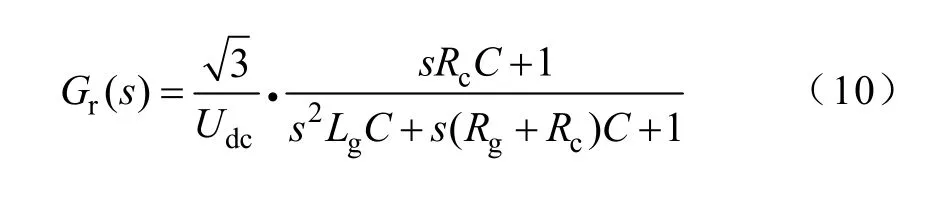
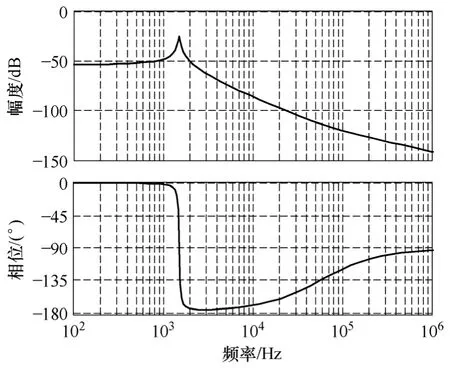
图5 电网电压前馈因子伯德图Fig.5 Bode diagram of grid voltage feed forward factor

可见，在谐振峰频率处需要较大的前馈作用。前馈的加入除了提高对电网的抗扰动能力，也对控制系统的暂态响应改善很大，实验表明可以消除并网瞬间起动电流的冲击。

由于电网谐波中占主导因素的是5 次、7 次谐波，在dq 下，根据坐标变换可知

式中，fr为旋转坐标下频率；fs对应静止坐标下频率；f0为电网频率。因此，在dq 系下的频率比实际频率小于50Hz。

PI 控制器虽然可以实现对基波（对应直流量）的无静差控制，但从图4 可见，在5 次、7 次，尤其7 次谐波频率处，对应图中300Hz 处，环路增益只有10dB，对该次谐波抑制能力很弱，为此引入了PR 谐振控制器，传统的PR 如下：

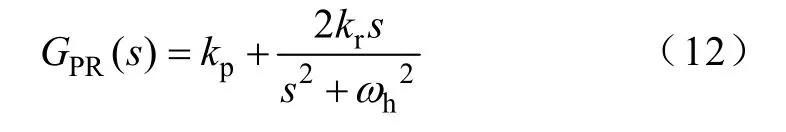
虽然在ωh处具有无穷大增益，但是其选频带极窄，在其他频率衰减严重，考虑到数字实现的误差和电网频率的波动，一般采用准PR

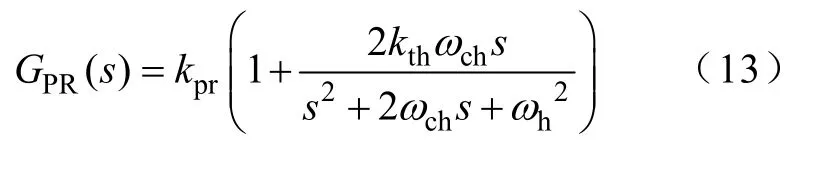
准PR 通过ωch项确定了选频带宽，可以避免上述问题，但是它的增益相比前者，减小了很多，因此如果舍弃PI，只用该PR 在三相静止坐标系下作为电流环控制，本质上也是有差控制，而在旋转坐标下，在PI 无静差控制的基础上，级联PR 作为特定谐波抑制，可以结合两者的优点，达到较好的电流控制质量，因此最终的控制器GC(s)如下：

本文中，主要采用PR 控制器来抑制7 次谐波，同时与5 次谐波作为对照。

选取ωh=2π×300，取ωch=0.4，kpr=1，kth=24，PI 级联PR 后，伯德图如图6 所示，可见对7 次谐波具有40dB 增益。

4 仿真及实验结果

控制算法在TMS320F2833X DSP 上实现完成，在一台100kW 三相光伏并网逆变装置上得以验证，Lf=0.2mH，Lg=78.3μH，C=47μF，开关频率5kHz，直流母线电压随日照变化而变化，100kW 光伏阵列MPPT 电压在500～720V，工频变压器隔离并网，电网线电压380V、50Hz。

图6 使用PI 级联PR 控制器补偿前后的开环 传递函数伯德图Fig.6 Bode diagram of open loop transfer function before and after compensation by using cascaded PI+PR controller

本实验用到的主要实验设备有日置3390 功率分析仪，安捷伦DSO7000 系列示波器和Fluke435电能质量分析仪。

图7 给出了在Matlab/Simulink 仿真下仿真结果。图7a 为100kW 满功率时并网电压电流波形，按纯有功逆变输出，功率因数为1；图7b 为各功率等级下，使用PR 抑制7 次谐波前后，并网电流谐波含量的仿真结果，以5 次、7 次谐波作为对照。

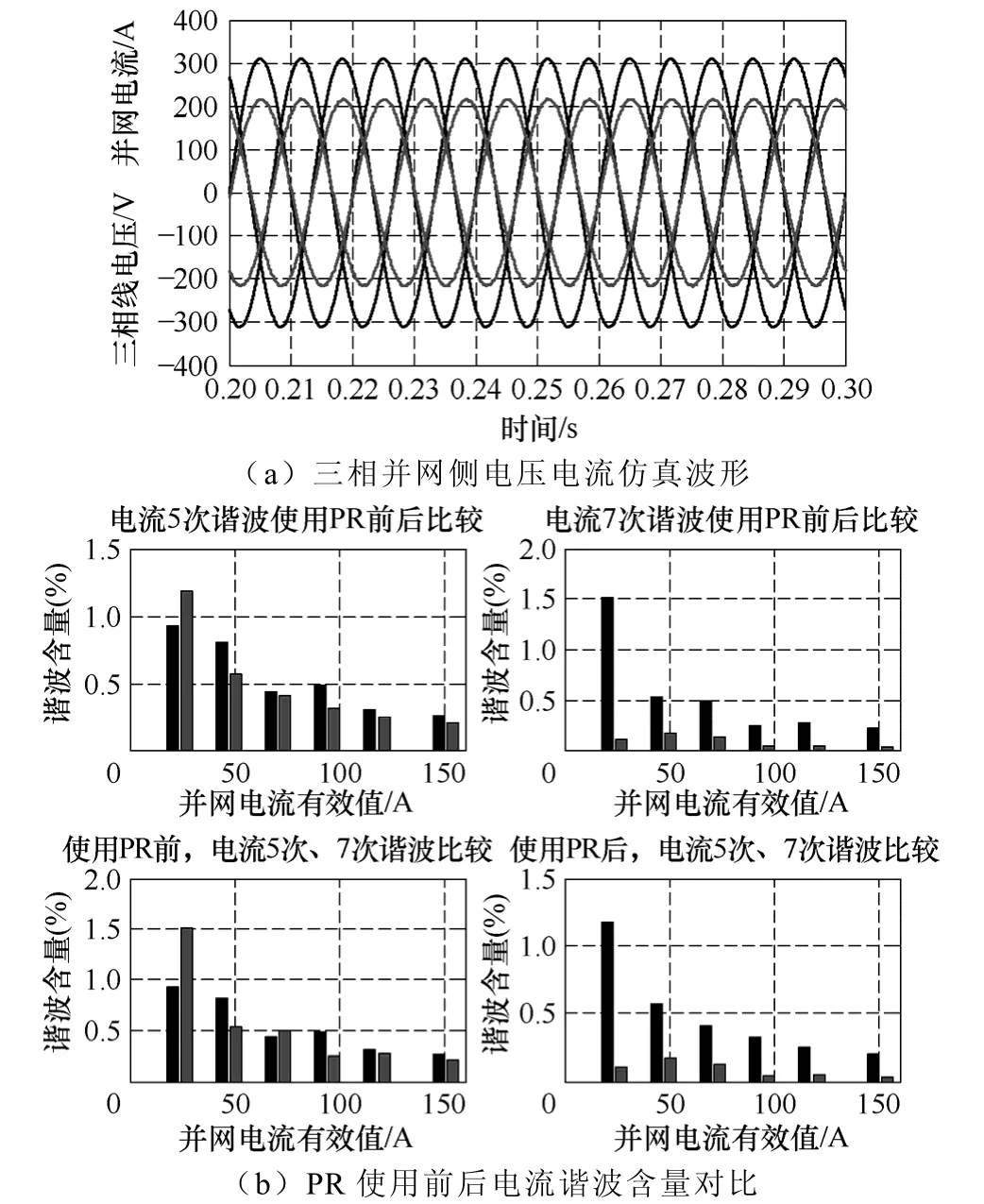
图7 并网逆变器仿真结果Fig.7 Simulation results of grid-connected inverter

实验结果见图8～图11，图8a 为不加电网前馈时并网瞬间起动电流和直流母线电压，图8b 为采用电网前馈后并网瞬间起动电流Id和母线电压。从图8b 中可见，当并网电流软起动时，电压前馈加速了电流环的响应速度，使得在并网瞬间，能够立刻跟踪电流软起动指令，输出相应占空比，解决了在图8a 中存在的由于并网瞬间占空比输出不足，逆变电压低于电网电压导致功率倒流及直流侧电容充电升压的问题。

图9 为PI 级联PR 加电网前馈控制下，并网输出电流63A 时，三相并网电压电流波形。图10 为此时THD 及5 次、7 次谐波含量对比，其中对7 次谐波采用了PR 控制。从对比可见，在dq 坐标系下，采用PR 特定消除7 次谐波，谐波含量减少了一半多，取得了很好的实验效果。

图11 为100kW 光伏阵列在80kW 输出时，并网电流谐波分析前50 次谐波含量表格，此时THD为1.21%。

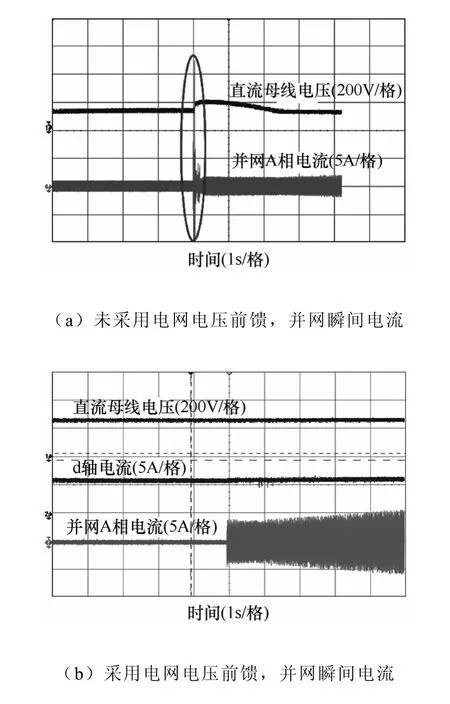
图8 电网电压前馈对并网瞬间的影响Fig.8 Influences of grid voltage feed forward on instantaneous state of grid connecting

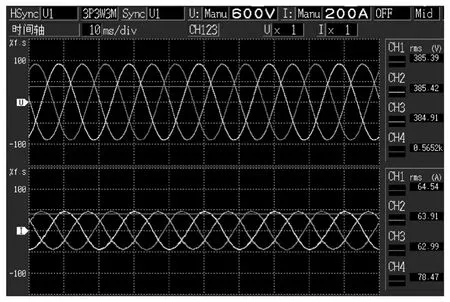
图9 PI+PR 下三相并网电压电流实验波形Fig.9 Experiment waveforms of three phase grid voltage and current under PI+PR and voltage feed forward controlling

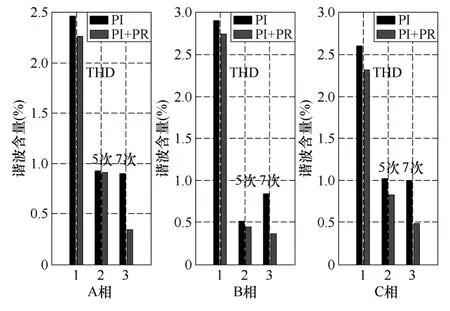
图10 三相并网电流谐波含量对比Fig.10 Contrast of three phase harmonics current

图11 输出功率80kW 时网侧电流谐波含量Fig.11 Harmonics Table of grid-side current at 80kW

5 结论

本文讨论了在三相光伏并网逆变设计中常用的控制方法，针对各自优缺点提出了在dq 旋转坐标系下PI 级联准PR 控制器的新思路，通过仿真和100kW光伏阵列并网实验，验证了该方法对基波的无静差跟踪和对特定谐波的有效抑制，对并网电流THD的明显削减，同时通过加入dq 下的电网电压前馈，验证了其对系统暂态特性的改善作用，解决了并网瞬间的电流冲击问题，希望本文的工作能给今后大功率光伏并网逆变器的设计和工程实践些许启迪。

[1]Karshenas Hamid R,Saghafi Hadi.Basic criteria in designing lcl filters for grid connected converters[C].IEEE International Symposium on Industrial Electronics,2006:1996-2000.

[2]Liu Fei,Zhou Yan,Duan Shanxu,et al.Parameter design of a two-current-loop controller used in a grid-connected inverter system with LCL filter[J].IEEE Transactions on Industrial Electronics,2009,56(11):4483-4491.

[3]Teodorescu R,Blaabjerg F,Borup U,et al.A new control structure for grid connected LCL PC inverters with zero steady state error and selective harmonic compensation[C].Applied Power Electronics Conference and Exposition,2004:580-586.

[4]Jung Eunsoo,Sul Seung Ki.Implementation of grid-connected single-phase inverter based on FPGA[C].Applied Power Electronics Conference and Exposition,2009:889-893.

[5]Timbus A V,Ciobotaru M,Teodorescu R,et al.Adaptive resonant controller for grid-connected converters in distributed power generation systems[C].Applied Power Electronics Conference and Exposition,2006:1601-1606.

[6]赵清林,郭小强,邬伟扬.单相逆变器并网控制技术研究[J].中国电机工程学报,2007,27(16):60-64.Zhao Qinglin,Guo Xiaoqiang,Wu Weiyang.Research on control strategy for single-phase grid-connected inverter[J].Proceedings of the CSEE,2007,27(16):60-64.

[7]Se Kyo Chung.A phase tracking system for three phase utility interface inverters[J].IEEE Transactions on Industrial Electronics,2000,15(3):431-438.

[8]Timbus A,Teodorescu R,Blaabjerg F,et al.Synchronization methods for three phase distributed power generation systems[C].Power Electronics Specialists Conference,2005:2474-2481.

[9]王兆安,黄俊.电力电子技术[M].北京:机械工业出版社,2000.

[10]Zhang Richard.High performance power converter systems for nonlinear and unbalanced load source[D].Blackburg,Virginia:Faculty of the Virginia Polytechnic Institute and State University,1998.

[11]Shen Guoqiao,Zhu Xuancai,Chen Min,et al.A new current feedback PR control strategy for connected vsi with an LCL filters[C].Applied Power Electronics Conference and Exposition,2009:1564-1569.

[12]Chen Yun,Liu Fei.Design and control for three phase grid connected photovoltaic inverter with LCL filter[C].IEEE Circuits and Systems International Conference on Testing and Diagnosis,2009:1-4.

[13]沈国桥,徐德鸿.LCL 滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报,2008,28(18):36-41.Shen Guoqiao,Xu Dehong.Current control for grid-connected inverters by splitting the capacitor of LCL filter[J].Proceedings of the CSEE,2008,28(18):36-41.