非稳态条件下壤中氡浓度数理模型探讨
2012-07-06葛良全邹功江李业强姜海静徐立鹏
葛良全 邹功江 谷 懿 李业强 姜海静 徐立鹏
(成都理工大学 地学核技术四川省重点实验室,成都610059)
壤中氡具有很强的运移能力,作为一种示踪元素被广泛应用在各个领域,如铀矿勘探、油气勘探、工程地质、地震预测等。壤中氡的多种运移作用中,扩散作用和对流作用至今仍被认为是氡运移的重要机制[1]。1987年,О.Б.Нещеткин在小钻孔中证明了氡气对流迁移是存在的[2];1974年Clements曾提出了一维数学模型[3];刘庆成等通过实验对一维模型运用扩散对流理论进行验证;1993年D.J.Holford等通过对地表裂隙氡气的运移模拟,提出了氡运移的二维模型[4]。刘菁华研究了活断层上覆盖层壤中氡运移的二维模型,并对其进行正演研究和反演拟合[5]。程业勋和刘庆成根据氡扩散作用与对流作用的迁移理论建立了地-空界面两侧地表介质和大气中氡浓度的定解问题,提出了在地-空界面上氡浓度连续的边界条件,并由此推导出壤中氡浓度与大气氡浓度的数学表达式[6]。以上是在不同空间和不同介质情况中,讨论氡在稳态条件下运移情况;但实际情况中氡浓度不仅和空间、介质有关,还随时间变化有所不同,即非稳态。壤中氡浓度受到压强和温度因素的影响,而压强和温度随时间周期性变化,所以氡浓度也随时间发生变化。1994年美国夏威夷大学C.Chen和D.M.Thomas,研究非稳态情况下氡运移受到土壤水分、土壤温度、大气压、降雨量和风速的影响,分别在3个不同深度测量,对影响因素做出曲线解释[7]。本文讨论了自然条件下氡扩散-对流作用,考虑压强、大气温度变化对壤中氡浓度的扰动,得到非稳态条件下壤中氡浓度表达式。
1 定解问题
1.1 壤中氡迁移方程
在天然土壤中含有一定量的放射性核素Ra,它们衰变后会形成射气,并影响土壤中射气浓度的分布规律。假设:土壤为无限厚、半无限大空间,土壤中U和Ra元素含量分布均匀。氡的运移仅考虑扩散、对流作用,且只考虑垂直迁移。取地面向下的方向建立x坐标,则在土壤的dx层中(图1),单位时间氡量的变化由3部分引起[1]:(1)从底面扩散、对流进入dx层的射气流量Q;(2)与从顶面出射的氡射气流量(Q+dQ);(3)dx层中从镭衰变引起射气的增加。
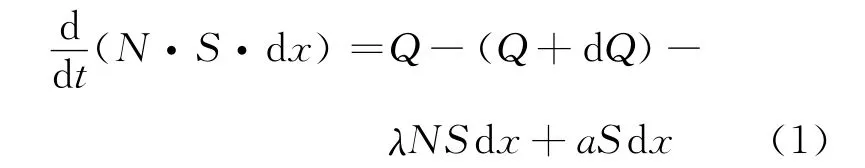
其中:N 为壤中氡射气浓度(Bq/cm3);S为单位层的表面积(cm2);Q为从底面流进入dx层的射气流量(Bq/s);dQ为dx层中氡射气自身衰变引起的减少;λ为222Rn的衰变常数(2.1×10-6s-1);a为土壤单位层厚单位时间内镭衰变产生的射气浓度(Bq/cm3·s)。

图1 半无限介质氡运移示意图Fig.1 Diagram of the semi-infinite medium radon transport
对(1)式化简可得[1]

式中:D为扩散系数,表征氡浓度差引起的氡运移能力的参数;v(t)为对流速度。
根据多孔介质中流体体系连续介质的Cauchy方程,对流速度由下式给出[8]
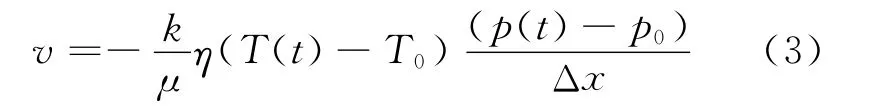
其中:k为多孔介质流体渗透系数(cm2);μ为多孔介质流体黏滞系数(Pa·s);η为流体膨胀系数;T0和T(t)分别是给定深度下t=0时刻和t时刻的温度;p0和p(t)分别是给定深度下t=0时刻和t时刻的压力。
根据实验中压力和温度数据,压力和温度都随时间呈明显的周期性变化,其变化周期T=12 h(图2)。由于土壤孔隙中氡气的对流作用是在温度差和压力差条件进行的,在同一深度处土壤孔隙中氡气浓度也随时间呈周期性的变化,可描述为
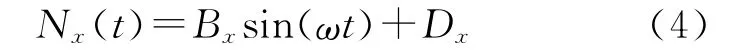
式中:Bx和Dx为待定系数;Bx表示在深度x处氡浓度呈正弦规律变化的振幅;Dx表示在深度x处在基准温度和压力下的氡浓度值;ω为角频率,ω=π/6。对上式求导有

将(5)式代入(2)式可得非稳态条件下土壤中氡浓度的运移方程

1.2 边界条件
(1)当土壤深度无限大时,即x→∞,N(x,t)为确定值。
(2)当x=0时,N=0。因为空气中氡浓度远小于壤中氡浓度,约小3个数量级,在地-空界面上可以认为土壤孔隙中氡浓度趋于0。

图2 1.4m和0.28m深度处土壤空气中大气压力与时间关系曲线Fig.2 The curves of the air pressure in soils at the depth of 1.4mand 0.28mvs times
2 壤中氡浓度表达式
应用上述边界条件对(6)式求解,可得非稳态条件下壤中氡浓度随时间和深度变化的数学表达式。
(6)式的一般解为
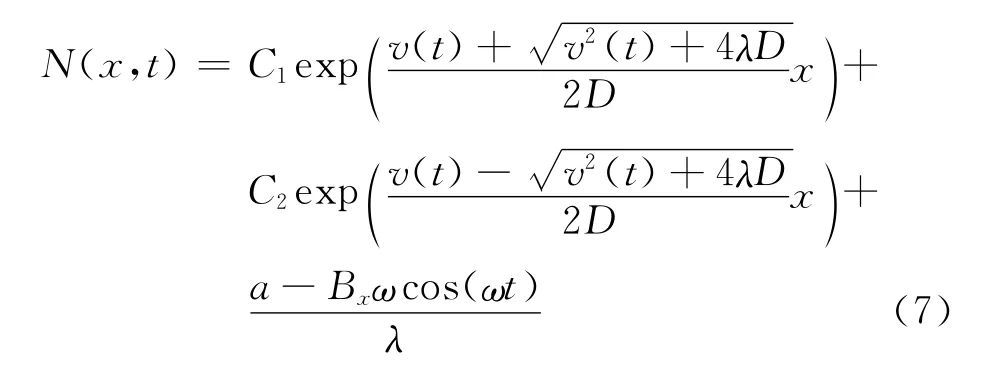
由边界条件(1),可得C1=0;
由边界条件(2),当x=0时,N=0,则

将C1和C2代入(7)式可得
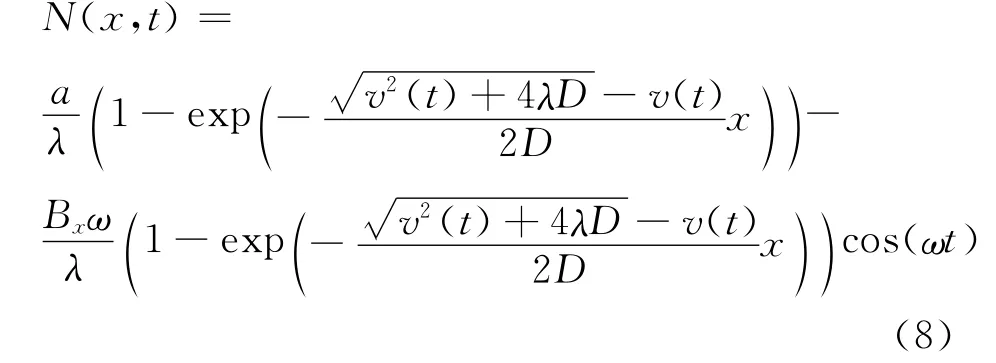
令

(8)式即是在镭-氡平衡条件下,非稳态壤中氡浓度随时间和深度变化的数学表达式。该式表明,在非稳态条件下,壤中氡浓度随深度的变化可表述为2种变化规律的合成。其一,由(8)式的第一项,氡浓度随深度增加呈饱和指数曲线规律增长,在x深度处的氡浓度可记为Dx。其二是(8)式第二项,氡浓度随时间呈余弦规律振荡,其振幅为Ax。该振幅一般由实验数据统计得出,可表述为在x深度处某一段时间内氡浓度变化极差统计平均值之1/2。
如果考虑氡的积累过程,如把仪器埋入土壤时,由于工程施工破坏了壤中氡平衡,氡及其子体在一段时间内积累,最后达到平衡。根据镭衰变氡的公式和氡子体积累公式[1]可得

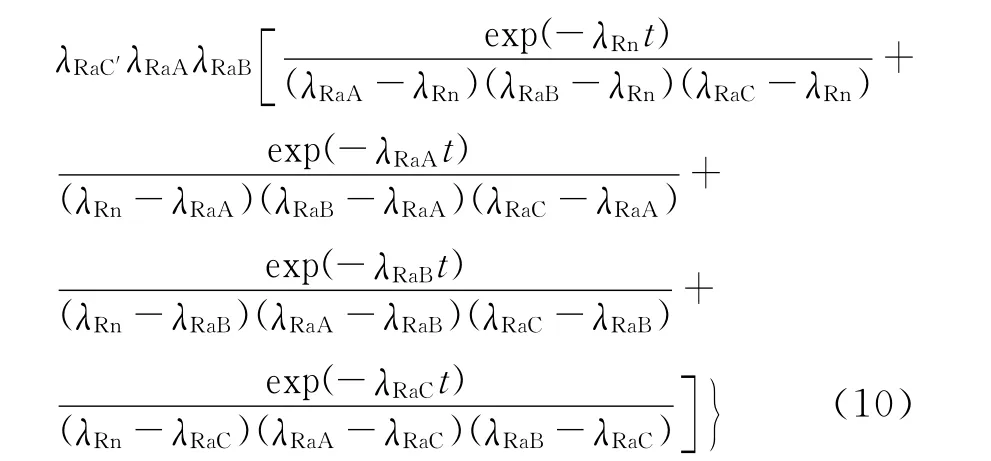
式中:λRaA、λRaB、λRaC分别为氡第一代、第二代和第三代子体半衰期;λRa为Ra的半衰期。
因此,在非稳态条件下,壤中氡浓度随时间和深度变化的数学表达式为
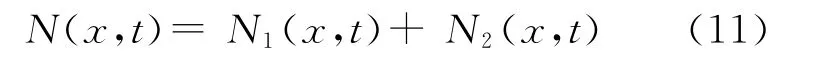
3 实验验证
3.1 实验场地与仪器设备
壤中非稳态氡浓度监测选择在成都理工大学校园内浮土覆盖很厚、气流稳定的天然绿地。测量布局见图3,在垂直方向上,分别距地表0.28m和1.4m的2个深度布点。实验采用本单位自行研制的IED-3000C型土壤连续测氡仪,并可实时测量温度和压力参数,2台测量机组埋入上述2点同时连续测量。在埋仪器的同时取土壤样,分别测定土壤密度、孔隙度、铀含量等参数,参数值如表1,表中其他参数为参考有关文献得到[9,10]。

图3 地下氡测量布局图Fig.3 Arrangement plan of the radon measurement devices in soils
3.2 参数设定
3.2.1 N0氡浓度的确定
N0表示土壤深处的射气浓度,当x→∞时,a/λ(记为N0)可表示为
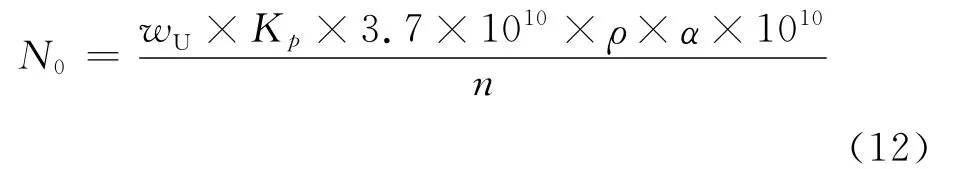
其中:wU为土壤中铀的质量分数;Kp为铀镭平衡系数;ρ为土壤密度(g/cm3);α为射气系数;n为土壤孔隙度。
3.2.2 A 值的确定
在0.28m和1.4m深度处A值的大小是利用该深度处自然产状条件下长期监测氡浓度变化极差数据的统计平均获得。根据20d壤中氡浓度连续监测结果,A0.28和 A1.4值分别为 192 和327,如表1所示。
3.3 结果与分析
将(3)式和(12)式代入(8)式,可得:
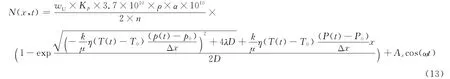
再将(13)式和(9)式代入(11)式,可获得在非稳态条件下,0.28m和1.4m深度处壤中氡浓度随时间变化的数学表达式。
图4是140cm深度处500h实验观测氡浓度值与理论预测值变化散点图。图中黑点为实验观测氡浓度值,红点为根据(11)式计算的理论预测氡浓度预测值。统计表明:在500h间隔内,实验观测壤中氡浓度值与理论预测值的相关系数为0.62。在氡积累过程中,理论值比实测值低,这是因为在实际仪器测量中会测到周围的α粒子;而模型是在理想化的情况下,从0开始积累α粒子,所以氡积累过程实测值比理论值要高。64h到254h之间,拟合情况很好,平均相对误差仅为-0.15%,说明(11)式可以表示壤中氡浓度的变化情况,进一步说明,壤中氡受到温度和压强的影响,随时间周期性变化,与(6)式确定的周期相符合。254h到342h之间,理论值高于实测值,平均相对误差高达30%,这主要是因为在此期间因下雨造成土壤湿度增大,土壤孔隙被水充填,影响氡的运移所致。在342h与400h期间,因天气下雨而停止监测工作;402h后如图2,实测值分布在理论值周围。
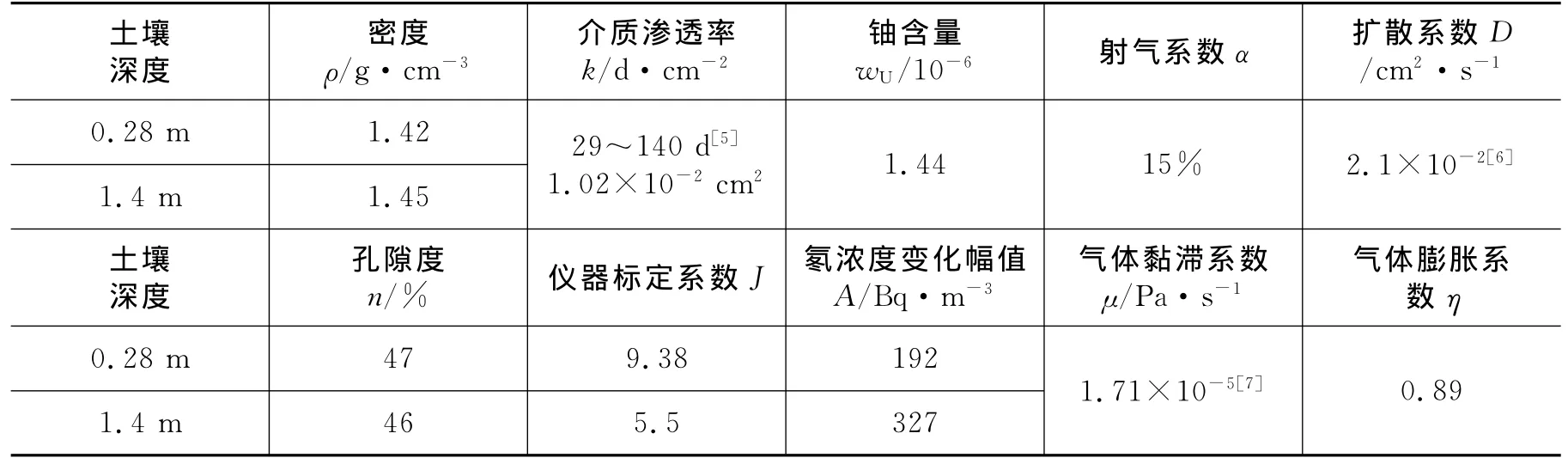
表1 壤中非稳态氡运移参数一览表Table 1 Related parameters of the radon migration in soils

图4 140cm深度氡浓度随时间变化曲线Fig.4 The curves of the concentration of radon in soils at 140cm depth vs times
4 结论
a.在扩散和对流作用下,考虑壤中氡浓度受到大气压力的影响因素,建立了非稳定条件下壤中氡运移的定解问题,确定了壤中氡浓度随时间和深度变化的数学表达式。
b.在镭-氡平衡条件下,非稳态壤中氡浓度随深度的变化可表述为2种变化规律的合成:(1)氡浓度随深度增加呈饱和指数曲线规律增长;(2)氡浓度随时间呈余弦规律振荡,其振幅为Ax,可表述为在x深度处某一段时间内氡浓度变化极差统计平均值之1/2。
c.经天然产状条件下壤中氡浓度的监测数据验证表明,在500h连续测量时间内,理论预测值与实验观测值的变化规律基本吻合,相关系数为0.62。
[1]成都地质学院三系.放射性方法勘查[M].北京:原子能出版社,1978:172-180.
[2]НещеткинОБ.氡迁移的机制问题[J].国外铀矿地质,1987(2):42.
[3]Holford D J,Schery S D,Wilson J L,et al.Modeling radon transport in dry cracked soil[J].Journal of Geophysical Research,1993,98(B1):567-580.
[4]Owczarski P C,Holford D J,Freeman H D,et al.Effects of changing water content and atmospheric pressure on radon flux from surfaces of five types[J].Geophysical Research Letters,1990,17(6):817-820.
[5]刘菁华.活断层上覆盖层中氡迁移的数值模拟及反演拟合[D].长春:吉林大学档案馆,2006.
[6]刘庆成,程业勋,章晔.环境中氡运移理论与计算方法研究[J].物探与化探,1998,22(2):149-152.
[7]Chen C,Thomas D M,Green R E J.Modeling of radon transport in unsaturated soil[J].Geophys Res,1995,100(B8):15517-15525.
[8]J.贝尔.多孔介质流体动力学[M].北京:中国建筑工业出版社,1983.
[9]贾文懿,方方,周蓉生,等.氡及其子体向上运移的内因团簇现象[J].成都理工学院学报,1999,26(2):171-175.
[10]乐仁昌,贾文懿,吴允平,等.氡运移实验研究与氡团簇运移机理[J].辐射防护,2002,22(3):175-181.
