基于改进神经网络的少齿差行星齿轮参数优化设计

2012-07-06吕俊峰陈小安赵孟娜

重庆理工大学学报(自然科学) 2012年2期

吕俊峰，陈小安，赵孟娜

(1.重庆大学机械传动国家重点实验室，重庆 4 00044;2.重庆理工大学重庆汽车学院，重庆 4 00054)

自20世纪20年代末德国出现渐开线少齿差行星传动以来，至今已有半个世纪。早期世界上许多著名学者对一齿差能否实现持否定态度，直到1949年前苏联H.A.斯克沃尔佐夫［1］在博士论文中从理论上解决了齿廓重迭干涉等难题并制成了实物后，才在全世界范围内开始了少齿差传动的研究制造。如今，少齿差行星齿轮传动以结构紧凑、体积小、质量轻、传动比范围大、效率较高等优点，被广泛应用于重工业及军事方面，但关于此类传动的优化设计方法仍然是学术界的研究热点和难点。传统的优化设计方法没有考虑各设计参数的模糊性和随机性，且存在局部最优现象，因此这种传统的优化设计方法的结果常常与实际情况存在一定出入。近年来广泛应用的BP神经网络优化方法能做到并行运算，具有一定的泛化能力和较好的容错性，但却存在着局部最小值域。本文所运用的算法结合了BP神经网络和模拟退火各自的优点，相比传统的单一神经网络，提出了一种较为合理的寻找最优解的少齿差行星齿轮传动可靠性优化设计方法。

1 优化设计少齿差行星传动数学模型

N形少齿差行星传动的简图如图1所示。其中1和2分别表示行星轮与中心轮，行星齿轮为外齿轮，中心轮为内齿轮，它们之间的齿数差通常为1～4个。

当这种少齿差行星齿轮传动用于减速时，是以系杆H为主动件。由于行星轮相对中心轮有偏差，故在传动时，行星轮1不仅要作公转还要作自传，因此，就需要1个能够传递两平行轴之间旋转运动的联轴器，即偏心输出机构V，以便把行星轮的自转输送出来。由于这种行星轮系是由1个中心齿轮K，1个系杆H和1个偏心输出机构V所构成的，故通常成为K－H－V型行星机构，简称N型行星机构。

与常规优化设计一样，目标函数、约束条件和设计变量是模糊优化设计数学模型的三要素。

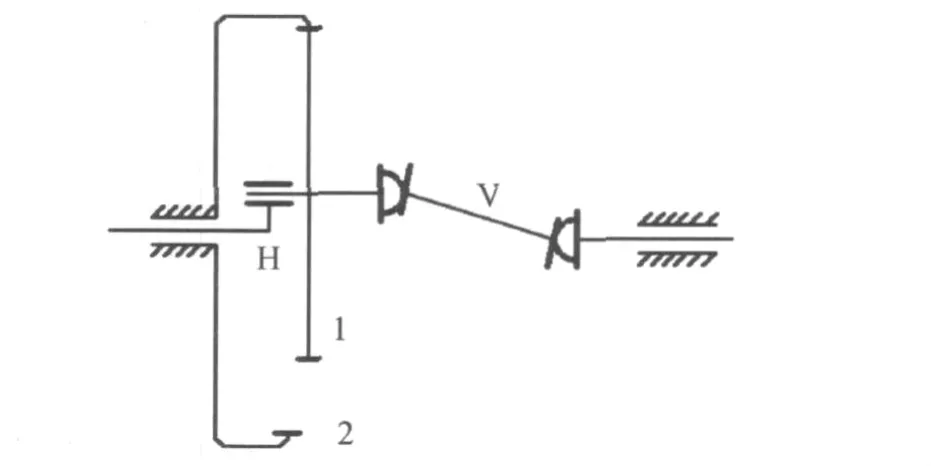
图1 N形少齿差行星传动简图

1.1 确定目标函数

为满足工业上对少齿差传动装置体积小、质量轻、传动效率高和工作寿命长的要求，通常取内齿轮和行星轮体积之和最小为目标函数，即

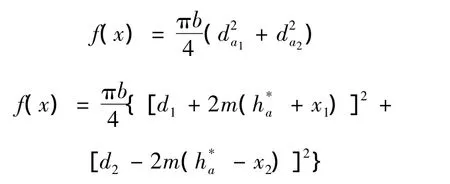
简化可得

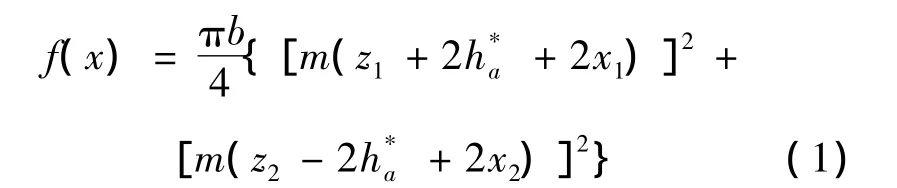
式中:b为齿宽;m为模数;z1和z2分别为行星轮和内齿的齿数为齿顶高系数;x1和x2是变位系数。

1.2 确定设计变量

由式(1)可知，设计少齿差行星齿轮传动需要确定的参数包括 b、m、z1、z2、、x1、x2。对于特定的某一N型齿行星齿轮传动，传动比i是给定的，因此只需选择参数z1、z2中的1个。故可以确定设计变量为

1.3 约束性能

1.3.1 强度约束

渐开线少齿差行星齿轮传动中内齿轮与行星轮曲率半径接近，接触面积大，接触应力小。一般来说，其齿面接触强度安全裕度远高于齿根弯曲强度裕度，主要的失效形式为轮齿折断。又因为齿轮传动从完全许用到完全不许用有一定的过度，即弯曲强度有一定的模糊性，因此具有一定的隶属函数，弯曲强度的模糊可靠度为

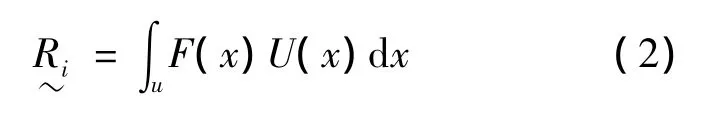
其中:U(x)是隶属函数;F(x)是概率密度函数。

U(x)许用弯曲应力模糊隶属函数为降半阶梯形分布其中a1、a2为许用应力。

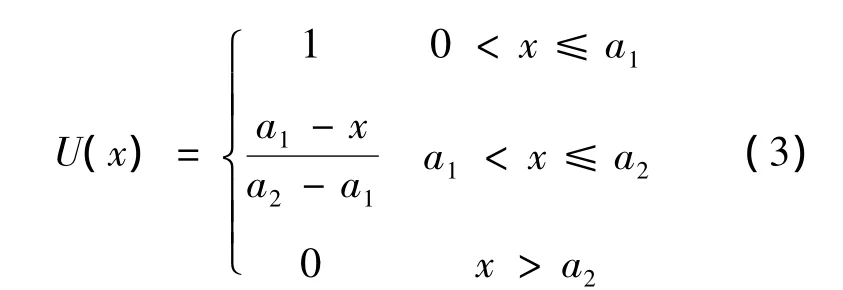
在K－H－V少齿差行星传动中，齿轮副弯曲应力近似于对数正态分布，其概率函数密度为

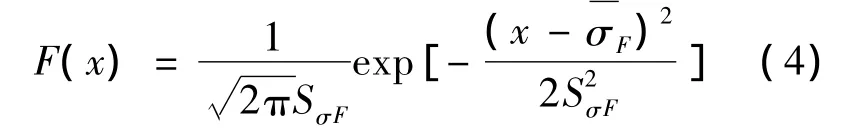
对N型少齿差行星齿轮，齿根弯曲应力计算式为

其中:K为载荷系数;YFa为齿形系数;YSa为应力修正系数;Yδ为重合度系数;Ft为圆周力;ψd为齿宽系数;m为模数，z为齿数。

因为轮齿齿根弯曲应力服从正态分布，根据式(5)，用变异系数法求弯曲应力的均值、变异系数和标准差:

取内齿轮、行星轮强度的要求可靠度R0=0.995，所以弯曲强度模糊可靠性约束条件为:

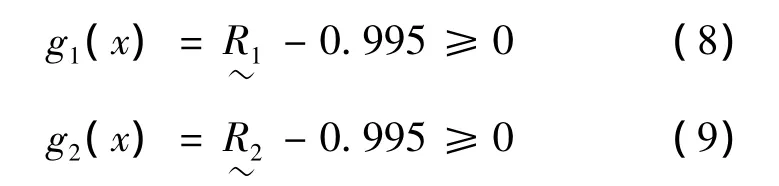
通过式(2)～(9)，即可得R1和R2。

1.3.2 性能约束

1)为保证连续传动平稳无冲击，齿轮副的重合度εa＞1，即应该满足不等式

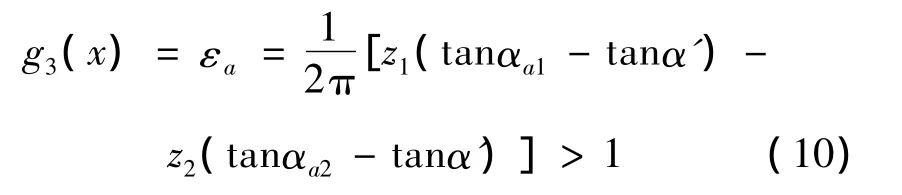
其中:αa1、αa2分别为行星轮和内齿轮顶圆压力角;α'是啮合角。

2)应保证不产生齿廓干涉，即应该满足不等式

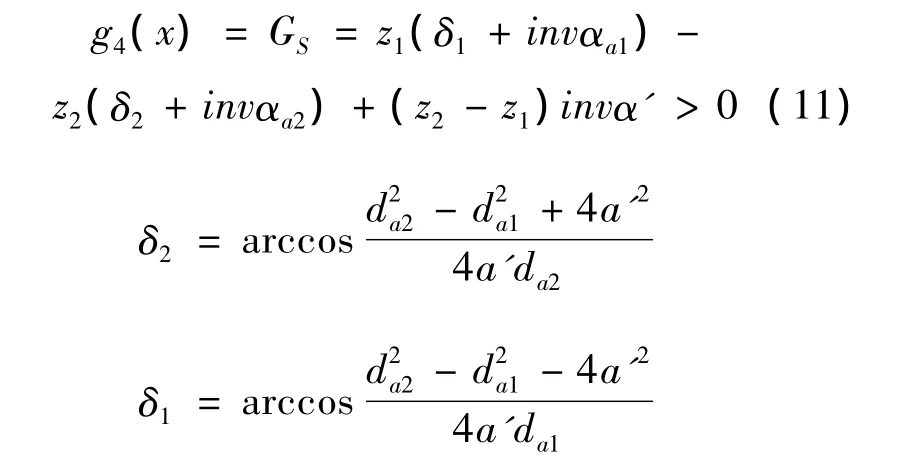
其中a'为齿轮副啮合中心距。

3)顶隙的约束条件为

式(12)中:ra1为行星轮齿顶圆半径;rf2为内齿轮齿根圆半径;c*为顶隙系数。

1.3.3 几何约束

为了避免切制内齿轮时产生范成顶切和避免过渡曲线干涉，作为选择齿轮加工刀具参数的约束条件，对设计变量确定模糊取值范围:

ai，共有 12 个约束函数

2 基于模拟退火的改进神经网络模型

在求解参数优化设计方面，人工神经网络中的前馈型BP网络，即误差逆传播网络是最流行、最常用的。它具有简单、易行、计算量小、并行性强的优点，但是它的显著缺点是学习算法的收敛速度慢、易陷入局部极值。而模拟退火算法在求解组合优化问题时引入了统计热力学的一些思想和概念，模拟其达到的最低能量状态为系统目标函数的解，并且可以通过“温度”和“能量”的设置使网络进行全局训练，但由于反复设置调整量，会使网络的学习速度很慢。因此提出一种新型的将模拟退火算法和BP网络结合起来的改进网络，可以保证在不降低网络学习速度的情况下找到全局极小点。

2.1 BP神经网络模型

BP神经网络结构如图2所示，共包括输入层、隐藏层、输出层。可设输入向量为n维，输出向量为m维，隐藏层有h个神经元。输入(隐藏)层的权矩阵为vij，表示输入层中的第i个神经元与隐藏层中的第j个神经元之间的权值，i=1，2，…，n，j=1，2，…，h。输出层的权矩阵为 wij，表示隐藏层中第i个神经元与输出层中的第j个神经元之间的权值，i=1，2，…，h，j=1，2，…，m。

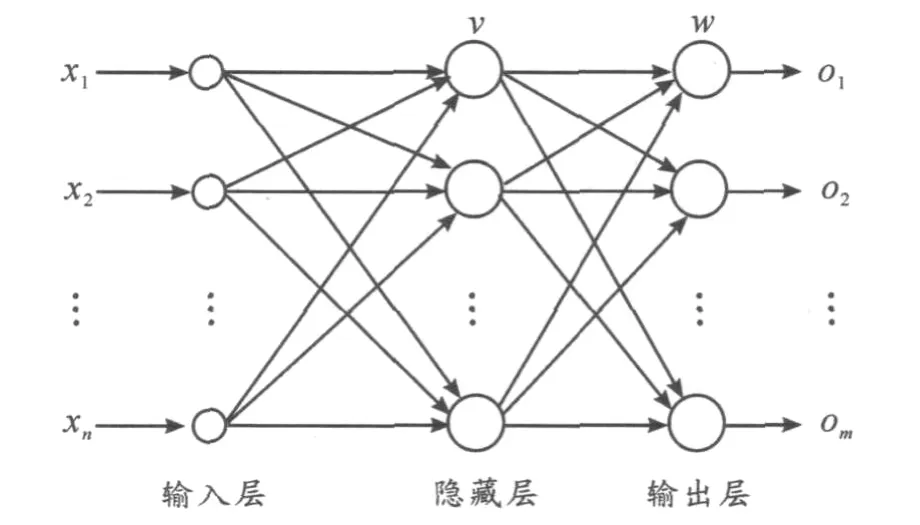
图2 BP神经网络结构

(X，Y)为样本集的一个样本，其中 X=(x1，x2，…，xn)，Y=(y1，y2，…，ym)。激励函数为

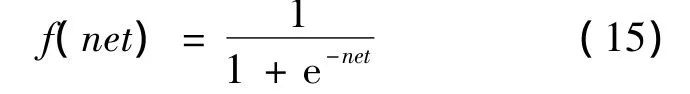
该样本对应的实际输出为 O=(o1，o2，…，om)，隐藏层的输出为 O'=(o'1，o'2，…，o'm)，其中

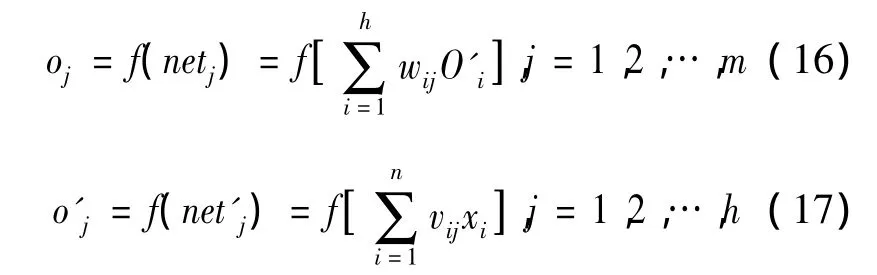
每个样本的误差测度为

整个样本集的误差测度为∑E。

根据负梯度方向下降法，输出层权值wij的调整量

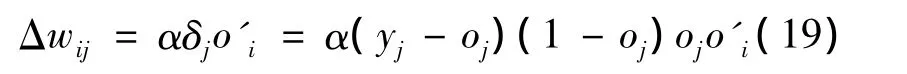
式中α为学习效率。

隐藏层连接权值vij的调整量

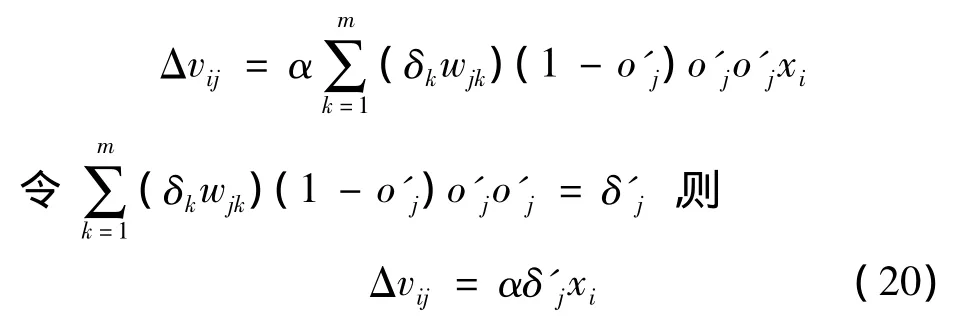
2.2 模拟退火算法改进BP神经网络

模拟退火算法最早的思想是由Metropolis在1953年提出的，1983年被Kirkpatrick等成功地引入了优化领域，其基本思想是模拟高温物体退火过程的方法来寻求优化问题的全局最优解。温度更新函数可按照给定的温度更新法则，利用如下冷却方程对系统降温:

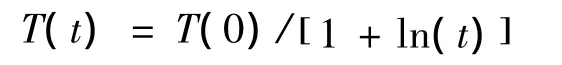
其中:T(0)为初始温度;t迭代步数。

结合这2种算法的优缺点，可将模拟退火算法引入BP网络，生成一种新的算法，描述如下:

1)设定初始温度T(0)，迭代次数t=0，M为循环次数。

2)输入训练样本，给定学习效率α，初始化各层权矩阵V和W。当t＜M时，循环执行t=t+1。选择一个样本，计算当前能量E。

3)若E1＜E，则接受该修改。

4)若 E1≥E，并且 p=exp(－ΔE/T)＞random(0，1)，则接受这次修改，否则进入下一次迭代计算。

5)若接受Δij，按式(21)进行变换。

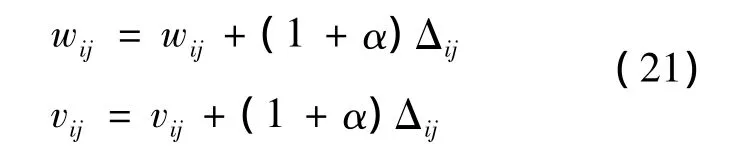
若不接受，则不重新生成调整量，按照式(19)和(20)得出的调整量作为本次权值的调整量，所有的样本按上述方法进行计算。同时按照给定的冷却方程对系统进行降温，直到冷却至给定的终止温度。

由上述算法可以看出，在模拟算法得出的调整量不被接受时，可以按单纯BP网络得出的调整量来调整权值，这样就避免了反复计算调整量，提高了学习速度，可更加迅速地找到全局最小点。

3 实验结果分析

本实验分析的是某挖掘机渐开线少齿差行星减速器，它的传动比 iz=60，输入轴转速 n1=1 200 r/min，输入功率 P=4 000 W，每天工作8 h，工作平稳。

该可靠模糊优化设计属于非对称模糊优化设计问题，因神经网络中的约束条件要求是常规约束条件，所以要采用最优化水平截集法求解，将模糊约束条件转化为常规约束条件，就可以使用常规的优化设计方法求解。现在根据二级模糊综合评判法，考虑设计水平、制造水平、材质好坏、使用条件、维修费用，确定最优截集水平λ*=0.80。

将训练样本输入网络结构进行训练，模拟退火参数及网络学习参数选择:初始温度为60℃，终止温度为1℃，循环次数为10 000，系统最大误差为0.01，单个样本最大误差为 0.001。运行Matlab进行计算，达到迭代次数或达到终止温度时迭代停止。可以得到优化参数，并根据得到的优化参数计算齿轮体积。为了便于比较，将传统设计结果、BP算法设计结果、改进的模拟退火人工神经网络结果设计分别进行了对比，如表1所示。