不同类型风电场对电网暂态稳定性的影响
2012-07-06田秀俊
李 伟,田秀俊,管 健
(吉林省电力勘测设计院,吉林 长春 130022)
近年来,随着风力发电技术的成熟和国家政策对可再生绿色能源的重视及支持,我国风电建设进入了一个快速发展时期。在东北、西北和东部沿海地区建设大容量并网型风力发电场成为大规模利用风能的主流方式。大规模风电场具有装机容量大、并网电压高的特点,该特点对电网的稳定运行带来较大的负面影响[1-2]。主要原因为:①适合大规模开发风电的地区一般处于电网末端,网架结构相对薄弱,风电大规模接入后可能出现电网电压水平下降、线路传输功率超出热极限、短路容量增加等现象;②风电机组采用不同于常规同步发电机的发电技术,在故障时其暂态特性与传统同步电机有很大不同。
大型风电场广泛采用异步风力发电机组,主要是笼式异步发电机组和双馈式异步发电机组。风电大规模开发初期,笼式机组因具有结构简单、运行可靠、价格低廉等特点成为风电场的主要发电机型。后期随着双馈感应电机 (DFIG)技术的成熟,该机型也被广泛采用。
目前,许多研究工作[1-6]都是单独分析笼式机或DFIG对系统稳定性影响,并未涉及二者之间的对比及区别。本文分别建立风力笼式机和DFIG机组的详细模型,对暂态稳定机理进行理论分析后,针对东北地区某一接入大量风电的实际系统,利用PSASP程序对不同风力机组模型在短路故障情况下的暂态行为进行仿真,得到不同模型下机组的临界切除时间 (CCT),研究比较笼式机和DFIG模型对电网稳定性的影响,以期对规划和运行有所指导,提高电网安全稳定运行水平。
1 风力发电机组动态模型
风力发电系统主要由风力机、传动箱、异步发电机、控制系统和机端并联电容器等组成。其中风力机叶片捕获风能并将其转换为机械能,通过传动设备驱动发电机将机械能转换为电能,控制系统实现对风力发电机组输出功率的调节和控制,以减小风电功率的波动。并网型风力发电场结构如图1所示。
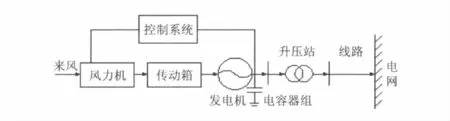
图1 风电机组结构示意图
1.1 风力机输出特性模型
风力机叶片从来风中捕获的风能Pw为[3-4]

式中:ρ为空气密度;R为风机叶片半径;Vw为风速;Vin和Vout分别表示风机的切入风速和切出风速;Vr为风电机组的额定风速;Pr为风电机组的额定有功出力;Cp为风能利用系数,是桨距角β和叶尖速率比 λ(λ=ωmR/Vw,ωm为风力机角速度)的函数,即Cp=f(β,λ)。
风电机组有功功率取决于风速的大小,不同结构及原理的风机有功功率不同。以变桨距风电机为例,稳态情况下,风速和输出功率之间的关系如图2所示。

图2 风机功率特性曲线
叶片机械转矩Mw为

式中:pl为发电机极对数。
叶片和轴系为非刚体连接,所以风能转矩从叶片传递到风力机轴系,类似于汽轮机的中间再热过程,具有一定的时滞效应,可用一阶惯性环节来表示:

式中:Th为时滞效应时间常数;p为微分算子,p=d/dt;Mm为风力机机械转矩。
1.2 机械传动轴系模型
根据研究问题性质和目的的不同,风力机轴系建模方法很多。在不需要分析应力分布和机械强度设计的情况下,可采用等效集中质量法[5]。
将风力机传动轴和发电机转子等效为一个质量块模型时,其运动方程的数学模型为

式中:Tj为机组惯性时间常数;Me为异步发电机的电磁转矩;Dm为机组转子阻尼系数。
考虑风力机轴系柔性的影响时,将风力机轴系和发电机转子各自等效为一个质量块,可建立两个质量块的同力机组轴系模型,其运动方程的数学模型为
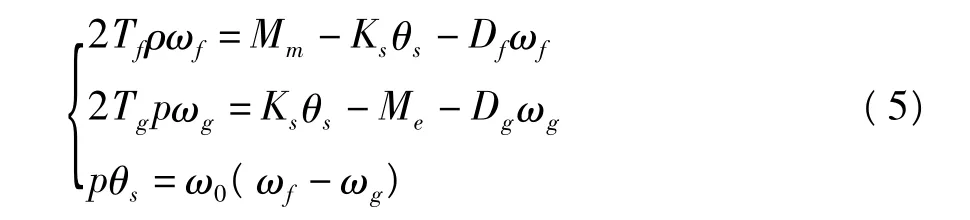
式中:Tf和Tg分别为风力机和发电机惯性时间常数;ωf和ωg分别为风力机和发电机角速度;Ks为轴系刚性系数,一般可通过轴系扭振频率估算;θs为风力机和发电机之间的扭转角;Df和Dg分别为风力机和发电机的阻尼系数;ω0为同步转速。
1.3 发电机模型
忽略定子电磁暂态过程,消去转子电流,利用暂态电抗后电势表示的异步电机的相量形式数学模型为

DFIG是在绕线式异步电机的基础上外加了连接转子滑环与定子的变流器及其控制系统,属于交流励磁异步化同步电机的一种[6]。DFIG为异步运行状态,通过变流器改变转子交流励磁电源的频率,使转速变化的转子产生的旋转磁场转速保持恒定并同步于定子磁场,把传统发电机机械与电气之间的刚性连接变为柔性连接。DFIG的相量形式数学模型为

2 异步机组暂态稳定机理分析
笼式机和DFIG理论上都属于异步机,在发电状态下可以不同转速运行,不存在同步发电机组的同步功角稳定问题。
正常运行时笼式机组需要系统无功功率励磁,故障期间加大了对无功功率的需求,稳定问题表现为系统电压的降低甚至崩溃;对机组自身而言,故障时转速上升以便存储由于系统故障而未能送出的风力机有功功率,当升高的转速与降低的电压超过临界点时,系统失去稳定。所以笼式机组稳定能力取决于临界电压和转速升高所决定的风机剩余有功功率。
DFIG通过恒功率因数控制,其稳态运行时功率因数为1,并不从系统吸收无功功率。并且由于交流励磁的存在,转子旋转磁场随时保持同步运行状态,放松了对转子转速的限制,使机组与电网的连接柔性化,为系统故障期间暂存风机的有功功率创造了条件,减少了风电机组对电网的冲击,有利于提高系统的暂态稳定性。
3 算例与分析
3.1 电网模型
以东北地区某实际电网为例,分析大容量风电场以不同模型接入系统后暂态稳定性对比及变化的情况。系统接线情况如图3所示。其中节点11为500 kV等值电网 (平衡点),节点3为风电接入点,节点1为已建成风电场,节点2为规划中的风电场,且节点1和2均接入电网末端。

图3 算例电网示意图
热电厂同步机组包含原动机、调速系统、励磁部分,发电机采用6阶模型;风电场采用第一节给出的式(1)、(2)、(3)、(4)和(6)组成笼式机组模型和(1)、(2)、(3)、(5)和(7)组成 DFIG 机组模型。负荷采用50%恒阻抗和50%感应电动机模型。
3.2 算例分析
基础运行方式:负荷930 MW,功率因数0.95,热电机组出力500 MW,两个风电场装机容量相等。
算例对两个风电场采用不同机组模型对电网暂态稳定性变化情况进行研究,包括2个方案。
3.2.1 方案A
计算条件包括运行方式、故障情况及风场模型3种,具体如下。
a. 运行方式:基础运行方式;
b. 故障分为2种,故障1:线路3-4单回发生三相短路;故障2:线路4-6单回发生三相短路;
c. 风电场类型分为3种。类型1:风电场1为笼式机组,风电场2为笼式机组;类型2:风电场1为笼式机组,风电场2为DFIG机组;类型3:风电场1为DFIG机组,风电场2为DFIG机组。
通过以上3种条件的组合,共对6个算例进行计算,其中故障1对应的故障CCT如表1所示。

表1 方案A中故障1对应的CCT结果
由表1可见,风机没有功率输出时,3种类型的故障CCT都为0.338 s,表明了风机接入前该系统在此运行方式下的稳定程度。当风机输出功率逐渐增大时,风场都选择笼式异步发电机时,系统故障CCT逐渐减小至0.193 s,说明笼式机的接入使系统的稳定性程度降低。风机是DFIG类型时,系统稳定程度反而随风机出力的增加而增加,直至出力到一定程度时才又减小,表明DFIG机组可以某种程度上提高系统的稳定性。风机为类型2时,系统稳定程度随出力增加而减小,但明显少于类型1,系统的稳定性介于类型1和类型3之间。由上可见,笼式风机不利于系统的稳定性,而DFIG风机有利于系统的稳定性,这一结论与前文的稳定机理的理论分析是一致的。
故障2对应的故障CCT如表2所示。

表2 方案A中故障2对应的CCT结果
由表2可见,当故障点发生变化时,笼式机组仍然减少系统的稳定程度,随风机出力增加,故障CCT逐渐减小到0.184 s。风机是DFIG类型时,故障CCT首先增加到0.345 s,随后减少到0.322 s,已经低于风机无出力时的0.338 s。对比表2与表1有:随着故障点的变化,笼式机不利于系统稳定性的程度加剧;故障1时DFIG机在出力400 MW时才进入到不利于系统稳定性的区间,而故障2时DFIG机在出力300 MW时就已进入到不利于系统稳定的区间,表明DFIG机有利于系统稳定性的程度减弱。
3.2.2 方案B
此方案运行方式是在基础方式的基础上将线路6-9双回线断开,其余计算条件和内容均与方案A相同,也是6个算例。故障1对应的故障CCT如表3所示。

表3 方案B中故障1对应的CCT结果
由表3可见,风机无出力时CCT为0.295 s,表明由于线路的退出,方案B的系统在风场接入前的稳定性比方案A要差。在此基础上接入风电场,当风场出力增加时,风场类型1、2和3都不利于系统的稳定性,但是程度不同,类型1的不利程度强些,类型3的不利程度相对弱些。
故障2对应的故障CCT如表4所示。
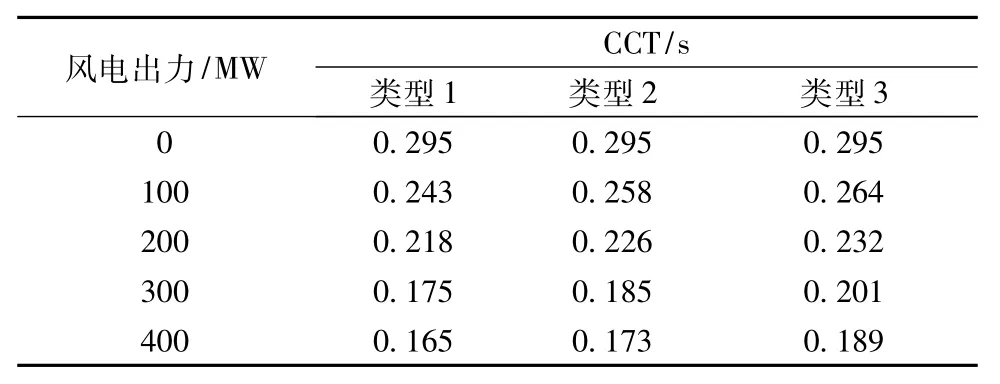
表4 方案B中故障2对应的CCT结果
当故障点发生变化时,表4与表3的区别在于类型1、2和3的风电场不利于系统稳定性的程度加剧,即使类型3不利于系统稳定性的程度稍弱,与表2与表1的对比相似。
4 结论
本文分析了采用笼式和DFIG异步发电机的大规模风电场接入系统时对系统暂态稳定性的影响,通过理论分析和对某一实际系统的仿真计算,得到以下结论。
a. 笼式机和DFIG都为异步发电机,不存在同步发电机组的同步功角稳定问题。
b. 笼式机组需要系统励磁,稳定问题表现为系统电压的降低甚至崩溃,笼式机组稳定能力取决于临界电压和转速升高所决定的风机剩余有功功率,不利于系统的稳定。DFIG通过交流励磁及控制,转子旋转磁场随时保持同步运行状态,使机组与电网的连接柔性化,理论上有利于系统的暂态稳定性。
c. 实际工作中确定DFIG机组风场的接入是否有利于系统的稳定性取决于风电接入点、电网结构、运行方式、故障类型等多种因素,必须经具体的仿真计算才能确定。推荐新接入风电场采用DFIG机组;如果接入点电网较为坚强,考虑经济性的前提下可以考虑笼式机组。
d. 今后研究重点是对大规模风电接入从电压和频率的波动角度分析风场极限穿透功率。
[1] 吴学光,张学成,印永华.异步风力发电系统动态稳定性分析的数学模型及其应用[J].电网技术,1998,22(6):68-72.
[2] 申 洪,梁 军,戴慧珠.基于电力系统暂态稳定分析的风电场穿透功率极限计算[J].电网技术,2002,26(8):8-11.
[3] 林 莉,孙才新,王永平,等.大容量风电场接入后电网电压稳定性的计算分析与控制策略[J].电网技术,2008,32(3):41-46.
[4] 田春笋,李琼林,宋晓凯.风电场建模及其对接入电网稳定性的影响分析 [J].电力系统保护与控制,2009,37(19):46-50.
[5] 李 辉,韩 力,赵 斌,等.风力机等效模型对机组暂态稳定性分析结果的影响 [J].电机工程学报,2008,28(17):105-111.
[6] 迟永宁,王伟胜,刘燕华,等.大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006,30(15):10-13.
