浅析金属丝编织层的重量计算

廖水平， 陈志榕

(广州广日电气设备有限公司，广东广州511447)

0 引言

金属丝编织层重量的计算，在《电线电缆手册》里提供了两个计算公式，这两个公式的计算结果存在着一定的偏差，本文就这两个公式的计算结果偏差所产生的原因进行了分析讨论，提出了解决的方法。

1 计算公式

《电线电缆手册》里提供了两个金属丝编织重量W的计算公式，分别如下:

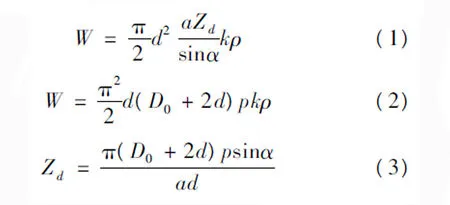
式中，p为每组金属丝的单向覆盖率(%);d为金属丝的直径(mm);α为编织角;a为编织总锭数的二分之一;k为编织的交叉系数;ρ为金属丝的材料密度;D0为编织前电线电缆外径(mm);Zd为每个锭子的金属丝根数。

2 计算结果与实际测量的比较

在计算一些编织屏蔽用的铜丝消耗时，与实际验证的数据不一样，利用式(1)的计算结果偏大，式(2)的偏小，偏差大小不一。例如在计算双绞屏蔽对称射频电缆的铜丝消耗时，按要求编织密度为85%，采用16锭编织机，取编织角为60°，按式(3)计算，每锭铜线为6根，根据《电线电缆手册》表7-5-3取单向覆盖率0.612 7，计算结果与实际测量的数据见表1。

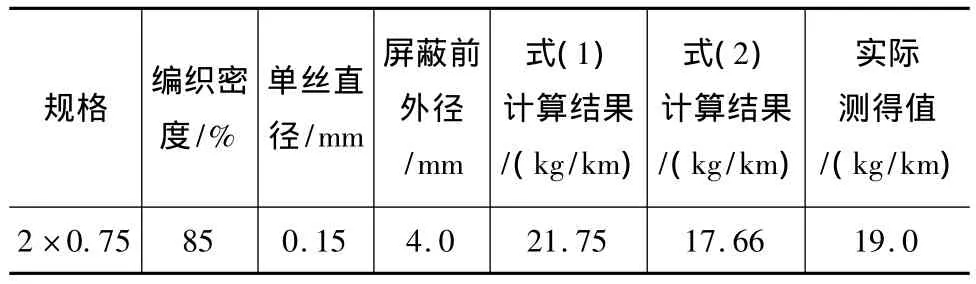
表1 双绞屏蔽对称射频电缆2×0.75的编织铜丝消耗与实测对照表

从表1可以看出，两个公式的计算结果相差了近4.1 kg/km，与实际测量值都有偏差，其中式(1)的计算结果偏大2.7 kg/km，式(2)偏小1.4 kg/km。

在表2中，也列出了不同屏蔽前外径按80%的编织密度、不同的编织角的要求进行计算的结果，每锭根数的计算按四舍五入取整。

从表2可以看出，两个公式对同一外径按相同的编织密度进行计算，其结果偏差大小不一。相同的编织密度根据不同的编织角计算结果的偏差也不一样，如表2中的第4项和第8项，而第4项是正偏差，偏差超过4%，第8项是负偏差，偏差不到2%。

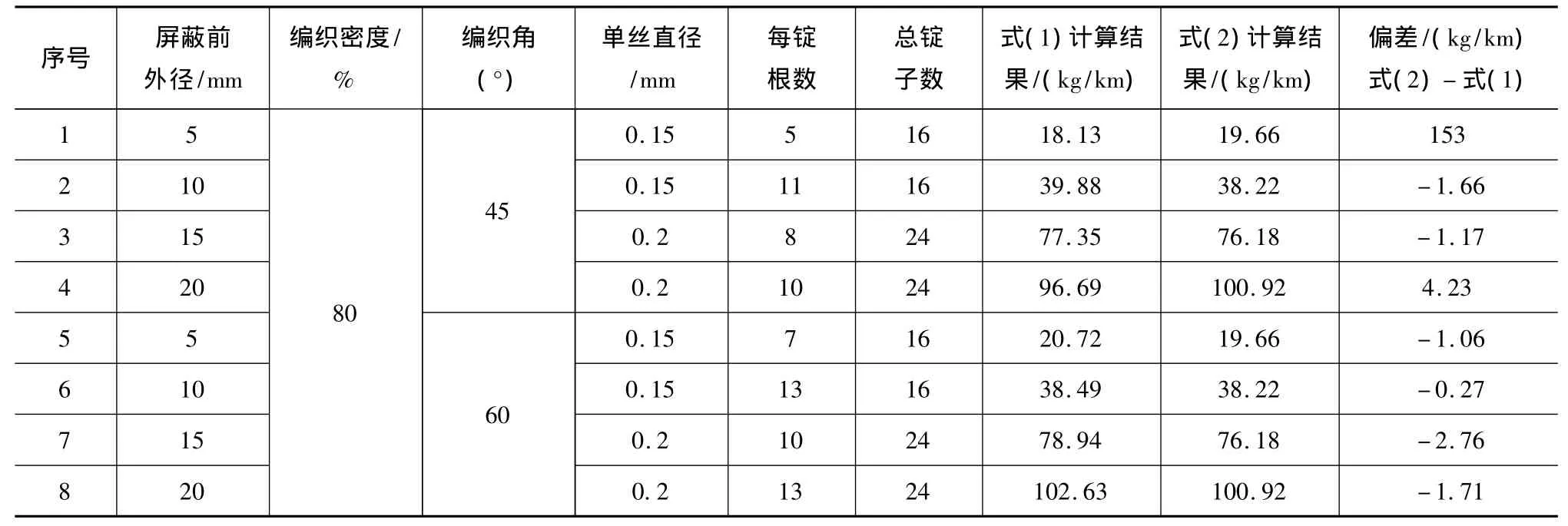
表2 不同屏蔽前直径的编织重量计算比较

另外，不同的编织密度，按相同的编织角进行计算的结果，两个公式的计算结果的偏差也不一样，有兴趣的读者可以自行计算验证。

3 原因分析

经分析，式(1)产生偏差的原因是在计算时，存在两个方面的不确定性:一是编织角是假定的，而非实际的或者说不准确的，比如假定的编织角45°，但实际的编织角会比45°大或者小，导致利用式(1)计算时计算结果出现偏差;二是在计算每锭金属丝根数Zd时，并不一定刚好是整数，在对Zd取整时，每个人可能都不一样，有的四舍五入，有的直接舍去小数点取整，有的是小数点进位取整，这也导致利用式(1)计算的结果出现偏差。例如在表2中，第4项按公式计算的单线根数为10.44，四舍五入后为10，比实际的计算值小，这时利用式(1)计算得到的编织重量比式(2)计算的结果小。偏差的大小与每锭根数的计算值取整后的整数之间的偏差有关，偏差越大，两个公式计算的结果的偏差也越大。当然，第二点原因与第一点原因在计算时可能会消除部分偏差，但也可能会扩大偏差。按照式(1)进行计算时，采用假定编织角为60°的计算结果与45°的计算结果存在偏差，也是由于在计算每锭根数时取整的值与实际值的偏差造成的。

式(2)实际上是将Zd的计算公式，代入式(1)的结果。式(2)出现偏差，其原因是单向覆盖率的问题。根据式(3)，计算确定Zd之后，由于取值的差异，见上段分析，实际单向覆盖率可能会偏大或偏小，式(2)的单向覆盖率只能说是为了计算确定每锭根数Zd的假定单向覆盖率，而不是实际的。

4 解决方法

为解决式(1)的计算问题，先根据式(3)确定每锭的金属丝根数后，再根据编织前的外径、锭子数、金属丝单线直径，按式(4)重新计算编织角正弦，将计算得到的结果代入式(1)进行铜线计算:

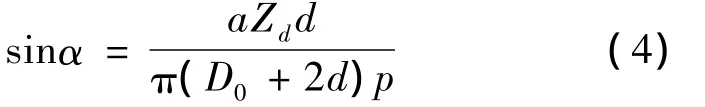
由式(4)计算出的正弦值才是实际编织角的正弦值，根据此值再计算编织角正切、编织节距、单向覆盖率及编织密度。此时计算得到的单向覆盖率与假定的覆盖率是不一致的，是实际的单向覆盖率，由此单向覆盖率计算出来的编织密度才是实际的编织密度，但与工艺要求的编织密度可能不一致。因此为了保证编织密度符合工艺要求，在锭子数确定、铜丝直径和假定编织角不变的情况下，通过不断调整假定单向覆盖率，来计算每锭根数、编织角正弦、编织角正切、编织节距、单向覆盖率及编织密度，直到计算结果的编织密度符合要求为止。此时计算得到的编织层重量与实际的是一致的，并利用计算的值确定生产工艺。在利用式(2)计算时，公式里的单向覆盖率应是调整到编织密度符合要求为止的假定单向覆盖率。此时，利用两个公式计算的结果才是一致的。单向覆盖率和编织密度的计算按GB/T 9330.1—2008第7.4条给定的公式。

5 计算验证

针对以上的分析，我们对双绞屏蔽对称射频电缆重新进行计算，锭子总数仍为16锭，假定的编织角为60°。经过反复计算，当编织密度达到85.02%时，假定的单向覆盖率为0.656，每锭铜丝根数为6，编织角为54.34°，节距为20.13 mm。将编织角为54.34°代入式(1)，单向覆盖率为0.656代入式(2)，计算结果及实际称重见表3。实际生产的节距为20.3 mm，测得的编织重量值略小于理论计算值，是因为编织前的双绞缆芯的间隙填充略小，不饱满、不充分，使外径略小于理论值所致。

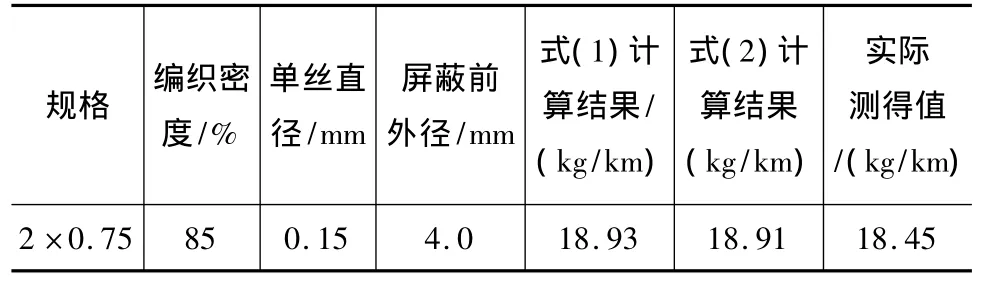
表3 调整后双绞屏蔽电缆2×0.75的铜丝消耗与实测对照表

表4为表2按原因分析后改进的计算方法计算的结果。

从表3和表4计算的结果看，两个公式计算的结果是一致的，而且不论采用多大的假定编织角，只要最后的编织密度相同，最后计算的编织层重量总是相同的。另外需要说明的是，表4中的式(2)的计算结果是依据假定单向覆盖率计算的结果，实际的单向覆盖率不能作为式(2)的计算依据。

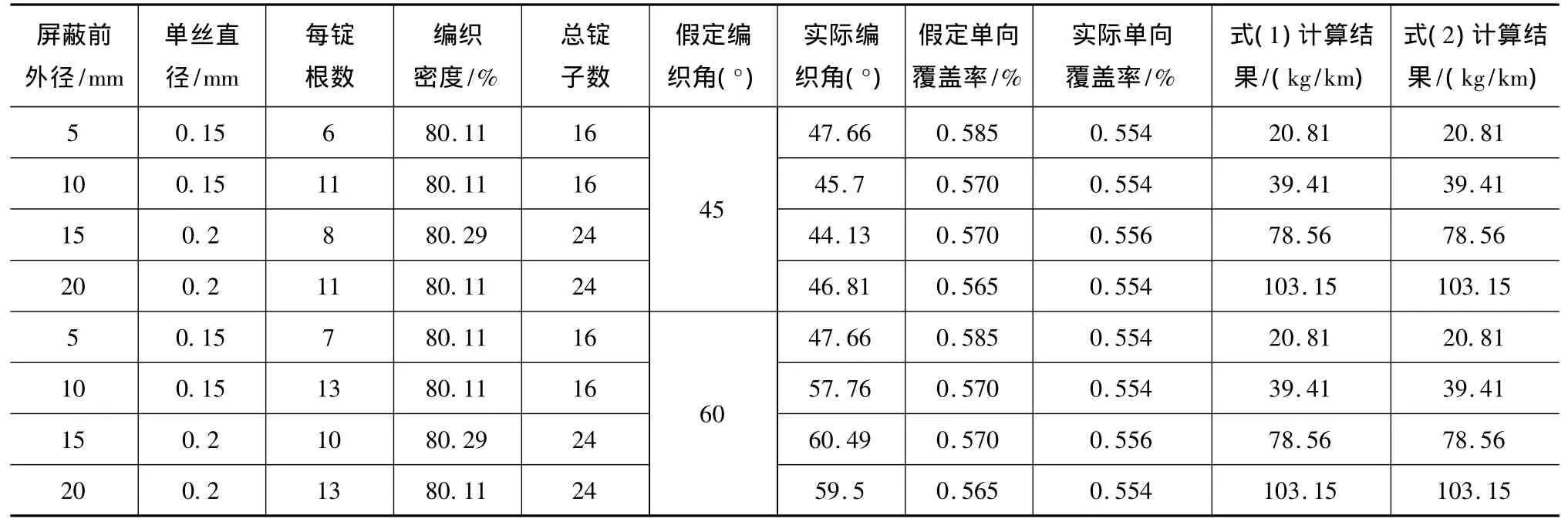
表4 调整后不同屏蔽前直径的编织重量计算比较

6 编织计算程序

要通过不断调整假定单向覆盖率或编织角来确定为满足编织密度所需的各项工艺参数，是一件比较烦琐的工作。而通过编写小程序来完成，既快捷又准确方便。下面介绍本人利用Visual Basic编写的一个小程序，供参考。界面如图1所示。

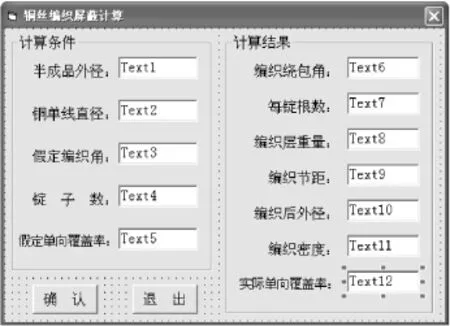
图1 程序操作界面

程序代码如下:

Private Sub Command1_Click()

Dim tg’定义正切

Dim a’定义编织角

Dim Sin定义正弦

Dim Cos’定义余弦

Dim K’定义单向覆盖率

Dim X

Dim Y

Text10.Text=Val(Text1.Text)+4*Text2.T’计算成品外径

a=Text3.Text*2*3.141 59/360’转化角度为弧度

tg=Tan(a)’计算假定编织角的正切

tg=Sqr(tg^2/(1+tg^2))’计算假定编织角的正切

Y=3.141 6*(Val(Text1.Text)+2*Val(Text2.Text))*Val(Text5.Text)*tg

X=(Val(Text4.Text)*Val(Text2.Text))

Text7.Text=Round(Y/X，0)’计算每锭根数

Sin=Text7.Text*Text4.Text*Text2.Text/(3.141 6*(Text1.Text+2*Text2.Text)*Text5.Text)’计算正弦值

Cos=Sqr(1－Sin^2)’计算余弦值

Text6.Text=Round(Atn(Sin/Cos)*360/2/3.141 6，2)’计算编织角

Text8.Text=Round(0.5*3.141 6*Text2.Text^2*Text4.Text*Text7.Text*1.02*8.89/Sin，2)’计算编织层重量

Text9.Text=Round(Text10.Text*(Sin/Cos)*3.14，2)’计算节距

K=Round(Text4.Text*Text7.Text*Text2.Text*Sqr(1+(3.141 6*Text10.Text/Text9.Text)^2)/(3.141 6*Text10.Text)，3)’

计算单向覆盖率

Text11.Text=Round((2*K －K^2)*100，3)’计算编织密度

Text12.Text=Round(K，2)

End Sub

在本程序中，只要输入半成品直径、铜单线直径、假定编织角、锭子数和假定单向覆盖率，点击确认按钮，即可得出计算结果。在计算条件里的锭子数是总锭子数的一半。

7 结束语

普通的电线电缆目前的利润是微薄的，在进行材料的定额计算时必须斤斤计较，尤其外径比较小的屏蔽电缆，每公里相差一两千克铜的话，对市场竞争力和经济效益都会产生巨大的影响，因此对计算的结果有必要进行比较、验证，对不妥的地方进行分析改进，以精确计算定额消耗。

［1］王春江主编.电线电缆手册(第一册)［M］.北京:机械工业出版社，2001.

［2］GB/T 9330.1—2008塑料绝缘控制电缆 第一部分:一般规定［S］.