雷电屏蔽模型在线路雷击分析中的应用

温 生，马 勇，周志成

（1.南京供电公司 江苏南京210041；2.江苏省电力公司电力科学研究院 江苏南京211103）

据统计，220 kV及以上输电线路雷电绕击跳闸次数占雷击跳闸总数的90%以上，雷电绕击是输电线路雷击跳闸的主要原因。输电线路发生雷电绕击跳闸主要是因雷电屏蔽失效造成的。雷电屏蔽是指通过设置避雷针、避雷线或者其他接闪装置，避免地面建筑物或者其他接地物体遭受直击雷的危害。利用雷电屏蔽分析模型可针对某一个具体的保护对象，确定该对象最佳的接闪装置配置方案，对其屏蔽系统可能存在的屏蔽失效率进行评估[1-3]。目前，雷电屏蔽分析模型主要分为三大类：几何法、电气几何模型法、物理模型法。

1 几何法

几何法是通过模拟试验结合运行经验建立起来的一种划分避雷针和避雷线保护范围的分析方法。由于雷云放电受很多偶然因素的影响，通常几何法确定的避雷针和避雷线保护范围是指具有0.1%雷击概率的空间范围[1，4]。

单支避雷针的保护范围如图1（a）所示，在高度为hx的水平面上，其保护半径rx为：

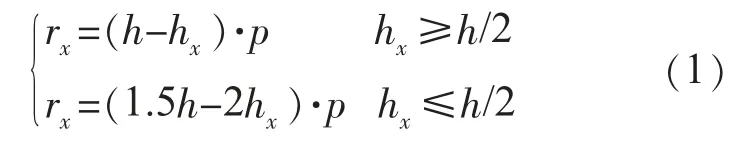
式中：h为避雷针的高度，m；hx为被保护物体的高度，m；p为高度影响系数（hx≤30 m时，p=1；30＜h≤120 m时，p=5.5/）。

对于单根避雷线，其保护范围如图1（b）所示，在高度为hx的水平面上，其保护区域rx为：

图1 几何法确定避雷针和避雷线的保护范围

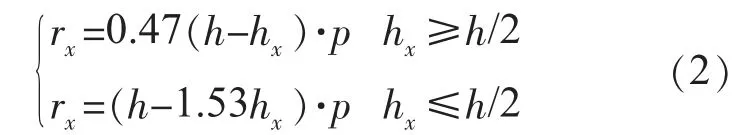
式中：h为避雷线的高度，m；hx为被保护物体的高度，m；p为高度影响系数。

由于几何法是在实验室条件下小模型试验得出的结果，与雷击真实的物理背景存在一定差异，可作为工程中的屏蔽设计方法。

2 电气几何模型法

电气几何模型利用击距概念使雷电屏蔽成为几何参数和电气参数相结合的分析模型，其将地闪放电特性与被保护物体的结构尺寸联系起来。该模型主要基于2个基本假设：（1）由雷云向地面发展的先导放电通道头部到达被击物体的临界击穿距离——击距以前，击中点是不确定的。（2）击距的大小与先导头部电位有关，因而与先导通道的电荷密度有关，根据理论研究和实验，击距与雷电流幅值有如下关系[4，5]：

式中：rx为击距，m；I为雷电流幅值，kA；a，b，c为系数。

自电气几何模型提出以来，Gold，Whitehead，Armstrong，Brown和Mousa等人为击距公式的修正开展了大量的工作，不断完善了击距公式，其主要结论如表1所示[4-6]。

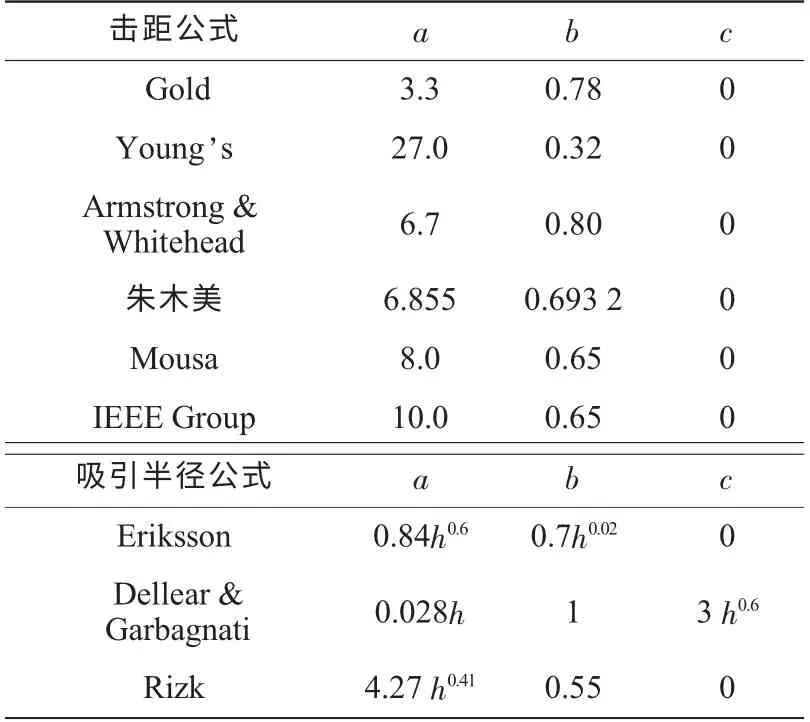
表1 不同学者和组织提出的击距和吸引半径公式

避雷针屏蔽示意图如图2（a）所示。避雷针是基于避雷针屏蔽模型（如图2（b）所示）建立的。220 kV输电一般都架设有避雷线，其雷电绕击的电器几何模型示意图如图2（c）所示。电器几何模型确定线路绕击暴露空间的基本思想：雷电下行先导头部自雷云向地面发展，在其未达到目的物临界击穿距离（击距）之前，其击中点是不确定的，若雷电下行先导先落入某地面物体击距范围内，即向该物体放电最终击中该物体。若假设雷电流幅值为Ii的下行先导，其可能的定位点为图2（c）中曲线CiBiAiDi，弧段和分别为以避雷线和导线为圆心，以击距r为半径的圆弧；直线AiDi为平行于大地、高度为击距r的直线。则若先导定位于弧段将击中避雷线，定位于弧段将击中导线，定位于直线段AiDi将击中大地，则弧段被称为导线暴露弧段，Dc被称为导线暴露距离。若线路处于良好屏蔽，则导线暴露弧和暴露距离长度将随着雷电流幅值的增加而减少；当暴露弧或者暴露距离减小至0时，对应此时的雷电流幅值为最大绕击电流Im，雷电流幅值大于此值的下行先导将不再绕击导线[5，6]。

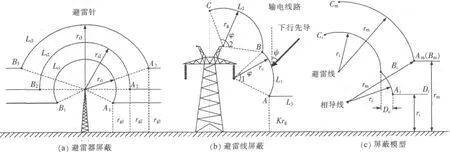
图2 电气几何模型分析示意图

电气几何模型不同于单纯的几何法，其是在现场观测的基础上结合理论研究建立的分析模型，通过线路几何结构、保护角和地形等参数分析线路绕击特性。引入击距的概念简化了雷击选择的最后过程，但击距的定义和取值依赖于现场观测数据的支撑和修正，故电气几何模型具有很强的工程应用性。

3 物理模型法

20世纪50年代以来，随着雷电观测、长间隙放电研究的进展以及放电击中点选择性影响因素的试验研究，下行地闪发展的基本物理过程已逐渐被认识。地闪是一种超长空气间隙放电，其空气间隙击穿过程主要包括：电极先导起始和发展、接地体上迎面先导的起始和发展、上下行先导间的相对运动和最后跃变过程。

物理模型在雷电观测数据的基础上，通过合理的假设和物理抽象，建立数学模型模拟下行地闪发展和最后击中点选择的整个物理过程。在雷击地面物体过程中，地面目的物上行先导的起始以及随后上下行先导间的相对运动在决定物体的引雷能力或吸引半径中发挥重要的作用。物理仿真模型包括：下行先导模型、迎面先导起始判据、迎面先导和下行先导的相对发展模型以及最后击穿判据等部分[6-8]。

3.1 Eriksson模型

Eriksson根据Gold提出的25 kA雷电流对应约1 C通道电荷量，并根据其在南非所开展的雷电观测结果，建立模型：

式中：I为回击电流峰值，kA；Q为地闪通道的电荷量，C。

假设雷云高度为5 km，Eriksson建立了下行先导模型，采用临界电晕半径法作为迎面先导的起始判据。与电气几何模型不同的是，Eriksson认为即使下行先导落入击距范围内，地面物体也不一定会成为雷击目的物，只有地面物体产生迎面先导后，与下行先导相遇，地闪最后击中该物体，否则地闪击中大地[6，7]。

通过引入下行先导速度vdown和上行先导速度vupward之比Kv，可以得到如图3中实线所示的不同相对运动速度比下的迎面先导拦截范围的曲线，该曲线与击距曲面交点确定的范围即为该物体的吸引半径Ra。

图3 Eriksson模型示意图

3.2 Dellear&Garbagnati模型

下行先导中总电荷量与雷电流幅值相关，电荷均匀分布。考虑下行先导有分支现象，地面目的物的上行先导起始主要受邻近一条先导分支通道影响，取下行先导头部几十米的通道电荷密度100μC/m；下行先导头部前方流注扩展范围为空间场强大于300 kV/m区域，下行先导沿最大场强方向传播[7，8]。

上行先导起始条件为具有临界电晕半径的电极的电晕起始条件，对于线形物，临界电晕半径为10 cm；对于棒型物，临界电晕半径为35 cm；上行先导通道线电荷密度为100μC/m，上行先导前方流注扩展的范围为空间场强大于500 kV/m的区域，上行先导沿最大场强方向传播[7，8]。

下行先导与上行先导相对发展速度之比在1～4之间变化，当上行先导刚起始时，vdescend/vupward=4.0；当达到最后跃变条件时，vdescend/vupward=1.0；最后跃变条件为：当上下行先导前方流注相遇或者下行先导前方流注抵达地面物体[7，8]。

3.3 Rizk模型

Rizk针对目的物上行先导起始判据这一问题，通过大量的实验，提出适于复杂间隙结构的先导起始判据，对于棒型物其先导起始判据为：

式中：Ui为下行先导在棒头部处感应电位，kV；h为棒型物的高度，m。对线性物其先导起始判据为[7，8]：

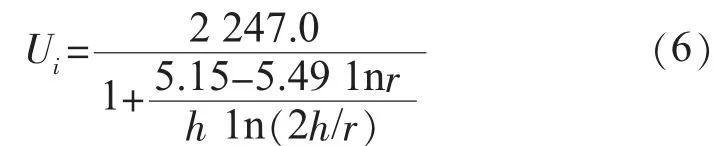
式中：Ui为下行先导在导线处感应电位，kV；h为线形物的高度，m。

假设下行先导始终垂直发展，从地面目的物上产生的上行先导始终朝向下行先导的头部发展；当下行先导头部高度低于上行先导仍未发生最后跃变时，判定下行先导将不会与此条上行先导相遇；上下行先导间的速度比取为1.0；当上下行先导间或者下行先导头部与地面物体表面间平均场强达到500 kV/m时，发生最后跃变。基于上述观点，Rizk首先建立了单导线的仿真模型，如图4（a）所示，仿真模型包括：下行先导、迎面先导起始和发展以及最后跃变等几个阶段[7，8]。根据单导线仿真结果提出导线吸引半径Da（I，h）的概念，其为导线高度和雷电流幅值的函数。如图4（b）所示，对于输电线路可分别计算得出避雷线吸引半径Dg（I，hg）和导线吸引半径Dc（I，hc），则导线的暴露距离为：

图4 Rizk模型示意图

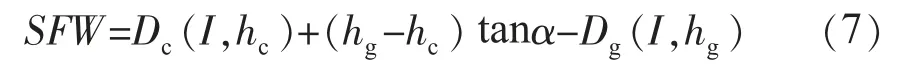
式中：SFW为暴露距离，m；α为保护角，（°）；hg为避雷线高度；hc为地线高度。

4 案例分析

近年来，江苏某些220 kV输电线路每年都发生雷电绕击故障，属于雷电易击线路。据统计数据可知，线路塔型主要采用鼓形塔FTSS1和猫头塔ZT2，如图5所示。按照几何法计算，三相导线均在避雷线的保护范围之内（即发生绕击的概率为0.1%）。采用几何模型、电气几何模型和物理模型分别计算杆塔的绕击性能，如表（2—4）所示，其中电气几何模型分别选用了Armstrong&Whitehead和IEEE Group推荐的击距公式，物理模型采用了Rizk模型的先导判据。

图5 220 kV交流线路典型杆塔示意图

由计算结果可知：

（1）几何法所得结果，各相导线均在避雷线保护范围，因为该方法来源于小模型试验，其保护范围是相对的，对实际工程指导作用有限；

（2）电气几何模型法计算结果主要取决于导线和避雷线的空间位置以及选用的击距公式，公式参数虽有差异，但结果差别不大；

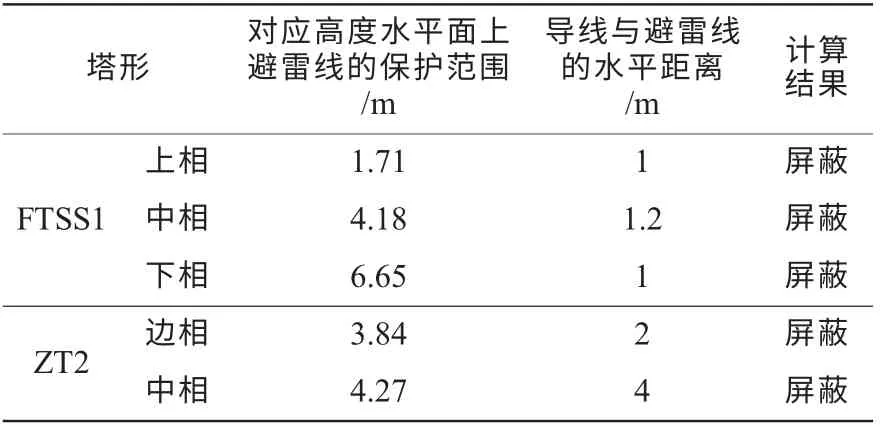
表2 几何模型法计算导线各相绕击性能结果

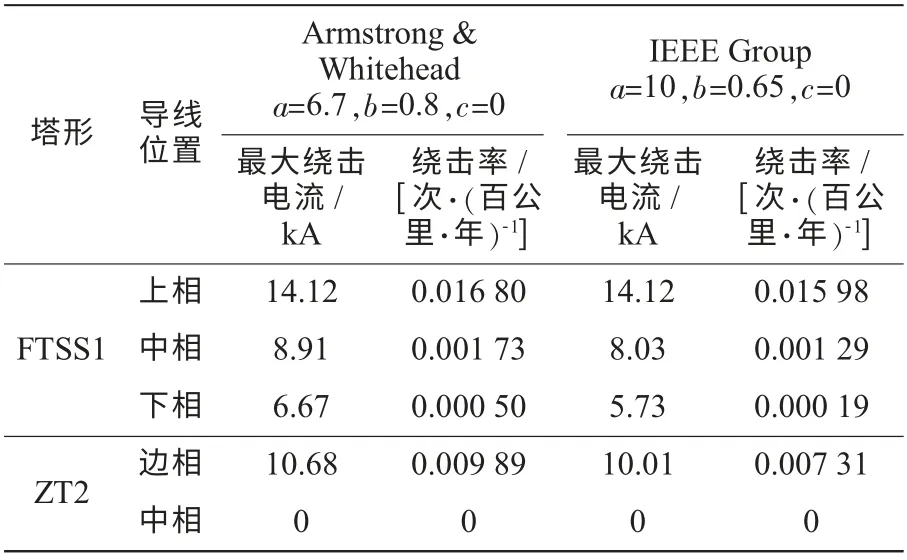
表3 电气几何模型法计算导线各相绕击性能结果

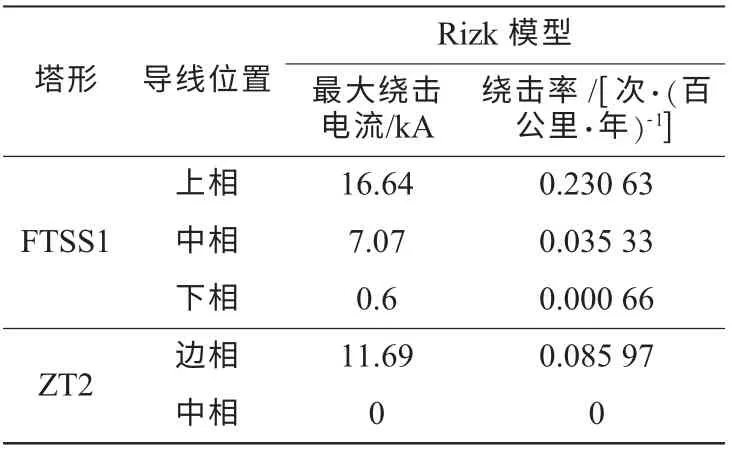
表4 物理模型Rizk先导判据计算导线各相绕击性能结果

（3）物理模型法考虑了雷电发展的过程，计算结果稍偏保守，建模与计算较复杂，但结果基本与电气几何模型相似；

（4）电气几何模型法和物理模型法的计算结果都表明鼓形塔的上相保护角最大，绕击概率最大，下相则相对较小，猫头塔中相不会绕击，所得基本规律一致。

5 结束语

（1）电气几何模型是将地闪放电特性与被保护物体的结构尺寸联系起来的雷电屏蔽模型，并得到大量的长距离间隙放电试验验证，各模型参数都具有较强的工程应用性；

（2）物理模型是在雷电观测数据的基础上，通过合理假设和物理抽象，建立数学模型模拟下行地闪发展和最后击中点选择的整个物理过程，较为真实反映了雷击过程，也能应用于线路雷击故障分析；

（3）电气几何模型和物理模型都较好分析了线路雷击故障原因。电气几何模型成功的重要原因之一是建立的雷电屏蔽分析模型基本符合工程实际。现有的物理仿真模型在数学上过于复杂，应适当简化仿真模型，并将物理仿真模型的计算结果不断修正电气几何模型，建立适用性更为广泛的雷电屏蔽分析模型。

[1]CURRIE J R,CHOY L A,DARVENIZA M.Monte Carlo Determination of the Frequency of Lightning Strokes and Shielding Failures[J].IEEE Transactions Power Apparatus Systems,1971,90：2305-2312.

[2]ERIKSSON A J.An Improved Electrogeometric Model for Transmission Line Shielding Analysis[J].IEEE Transactions on Power Delivery.1987(2)：871-886.

[3]GOLD R H,LEE W R.Death by Lightning[J].Proc IEE,1976,123：1163-1180.

[4]MOUSA,A M,SRIVASTAVA,K D.The Lightning Performance of Unshielded Steel-structure Transmission lines[J].IEEETransaction on Power Delivery,1989,4(1)：437-445.

[5]RIZK,F A M.Modeling of Transmission Line Exposure to Direct Lightning Strokes[J].IEEE Transactions on Power Delivery,1990,5(4)：1983-1997

[6]DELLEARL,GARBAGNATIE.Lightning Stroke Simulation by Means of the Leader Progression Model[J].IEEE Transactionson Power Delivery,1997,06(1)：2009-2022.

[7]ARMSTRONGH R,WHITEHEAD,ER.Field and Analytical Studies of Transmission Line Shielding[J].IEEETransactions Power Apparatus Systems,1968(1)：270-281.

[8]TAKATOSHI Shindo,ISAMU Kishizima,TOSHIO Suzuki.Flashover Characteristics of Air Gaps Under Partly Chopped Waves[J].IEEE Transactions on Power Delivery,1988,3(4)：1887-1891.