非线性机械系统PID控制渐近稳定性分析

马唯一

1.上海市采埃孚转向系统有限公司，上海 200062

2.上海交通大学自动化系，上海 200240

虽然当前控制理论与技术实现了持续的发展和进步，同时人们也提出了不同的非线性比例的积分和微分方程，有效改善了传统线性PID品质，但大多数的实际机械控制系统依旧采用传统的线性PID进行控制。而PID控制的非线性机械系统的稳定性分析一直是研究中的难点。

Arimoto提出了不确定的非线性机械系统PID局部控制趋向稳定性，而Kelly则提出根据饱和函数在实践中的引入明确了非线性不确定机械系统控制的全局渐进稳定性。相应的专家还了解到自适应饱和P加D控制过程中所呈现的机械系统全局稳定性特点。根据近期的文献研究了解到，专业的研究者所提出的新型的饱和函数，有效证明了P加D饱和同步误差的非线性控制机器人系统的全局渐进稳定特点。

1 机械系统动力学模型与特性

n自由度的自由度旋转关节非线性机械系统动力学模型描述如下：

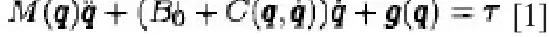
上述公式中，q为关节位置， 为速度矢量， 为加速度矢量，M（q）为对称正定惯性矩阵，而B0为关节线性阻尼摩擦力矩阵，C(q，)为哥氏力以及离心力矩阵，而g（q）是重力向量，U(q)是由于重力而形成的势能，而则是力矩控制矢量。

非线性机械系统一般具有一下所示的结构特性：

1）当B0，实际上也是线性阻尼矩阵为对角正定矩阵，惯性矩阵保持对称正定且并非无限，是有界的，其范围满足如下关系式：

其中的λm（M）以及λm(M)表示的是在M（q）矩阵中的最小特征值和最大特征值。

2）对于特定的qd以及任意的q以及α＞0，有一个恒定的对角正定矩阵保证下列关系式成立：

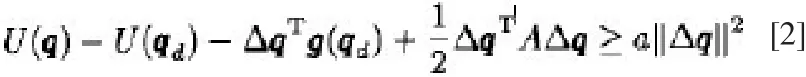
上述公式中Δq= q- qd为关节误差，而qd与q分别为期望以及实际的位置。

在实际的分析过程中，也就是公式中，对于任意的qd，也就的任意给定的期望位置，设计出线性PID控制器，通过综合的考量能与任何的模型信息适用，同时实现了非线性机械系统渐进稳定性位置的控制，从而致使非线性机械系统从初始的位置渐进稳定达到目标状态。

2 非线性机械系统PID控制渐进稳定性分析

2.1 传统线性控制半全局渐近稳定性

传统PID线性控制:

公式中的Kp+Ki为恒定对角正比例，而Kd为微分增益矩阵；Ki为积分增益矩阵。

将上述两个公式带入非线性机械系统的动力学模型后，可得出闭环系统的方程如下：

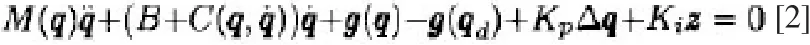
其中B=B0+Kd，通过上述公式，可得知ΔqT TzT为相应系统中唯一静态平衡点。

根据对传统线性PID控制的非线性机械系统的分析，可得出相应的定理：

根据非线性机械系统模型定义，传统线性PID控制系统的应用过程中，通过传统控制器的比例与微分增益参数适宜的不等式方程的设定和完善，那么系统的位置误差处于半全局的渐进收敛状态。也就的存在稳定的吸引域保证

由于公式所表示的Lyapunov函数V保持正定的。并且函数V的值将顺着闭环系统实现了时间倒数在平衡点附近内部吸引域的半负定。同时实际上值为零实际上也是Δq的值为零以及q•的值为零。根据LaSalle的不变性原理可了解到，吸引域D的值使处于其吸引域内部的初始值都将渐进稳定实现平衡位置的收敛。这似乎达到了局部渐进稳定的结果，然而实际上影响吸引域大小的常数值没有出现在非机械系统的控制器中，这个影响的正常数值大小可随意自定。同时也是吸引域的大小为整体的状态空间体系，由此，根据相关学者的相似讨论可推算出闭环系统的半全局渐进的稳定性特点。

2.2 改进后的非线性PID控制的全局渐近稳定性

根据相应的仿真模拟实验可知，改善完成之后的NPI-D控制器当中，控制系统中的等价比例的控制参数小于或者等于线性PID的控制参数，非线性机械系统控制器的位置和误差可根据仿真试验的结果看出，在通过了初始控制值的误差暂时状态过渡完成后，机器人系统位置控制误差逐渐接近零。同时实现改善后的非线性机械控制系统，也就是NPI-D系统，与传统的PID控制系统相比具有更快的反应速度。根据推算的理论体系和结论明确到，本论文提出的非线性机械系统NPI-D控制器的改进措施引入了较新的且将小误差放大的饱和函数，从而明确了在较小的控制增益状况下依旧能实现较快的过渡过程。为了保证非线性机械系统全局区域稳定性而采取的，通常所用的双曲余切函数无法放大误差，为了实现满意的系统过渡，机械系统中的比例以及积分的增益都相对大一些。

首先通过相类似的势能函数，实现对相应系统稳定性特点的推导：

针对近似的势能函数求导可得出非线性的饱和函数如下所示：

通过简单的运算可证明上述引理的成立。

应用势能函数针对x求导得出的非线性饱和函数，相应的非线性PI加D的控制器可表述为如下公式：

其中的Kp、Kd、Ki的值未恒定对角正定增益矩阵，可是实现如下矢量的定义：

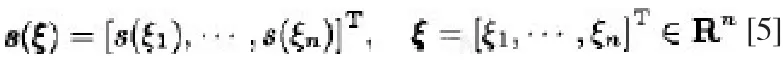
同时引入一定的矢量值：

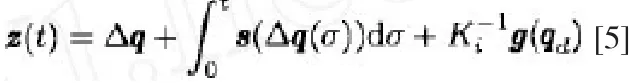
将上述公式代入近似势能函数可得出闭环的系统方程为：

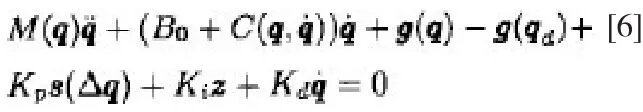
对于公式中所控制的闭环系统，可推出如下定理：

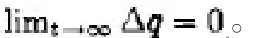
3 结论

通过对相应线性控制的非线性机械系统渐进稳定的分析，清晰明确地回答了这一开放性问题。虽然并没有对线性控制全局的渐进稳定性进行阐述，但实际证明了实际机械系统中的半全局的渐进稳定性，同时在传统的线性PID控制半全局渐进稳定性的分析基础之上，提出了改进的NPI-D控制体系，通过相应专业理论的应用证明了闭环系统呈现全局渐进稳定性，通过实际的实例进一步表明了理论分析结果的正确和有效。

[1]苏玉鑫，郑春红，Peter C.Müller.非线性机械系统PID控制渐近稳定性分析[J].自动化学报，2008(12).

[2]苏玉鑫，段宝岩.一种新型非线性PID控制器[J].控制与决策，2003(1).

[3]赵国生，魏志纲.基于非线性PID控制的三相有源滤波器[J].郑州大学学报(工学版)，2005(2).

[4]尚宏，陈志敏，任永平.一种新型非线性PID控制器及其参数设计[J].控制理论与应用，2009(4) .

[5]任廷志，吴忠强.非线性机械系统的模糊保代价控制[J].中国机械工程， 2003(19).

[6]李祖欣，蒋云良.一种新型模糊非线性PID控制器[J].信息与控制，2004(5).