基于ARMA的高精度GPS多普勒估计

杨晓波

（石家庄职业技术学院电子工程系 河北 石家庄 050081）

0 引言

GPS接收机在冷启动的情况下，对于接收机要进行码相位和载波多普勒的二维搜索，当对于卫星轨道没有任何先验知识的情况下，这个搜索范围是很大的，例如，对于地面静止的GPS接收机，不确定的多普勒范围是±5kHz[1]，对于积分时间为1ms的传统接收机，多普勒分为21个500Hz的频率单元，500Hz对于PLL带宽来说多普勒估计太过粗糙[2]，在一些接收机中，以FLL辅助PLL，先以带宽较大的FLL将载波频率估计锁定到PLL的捕捉频率范围，然后由FLL传递到PLL跟踪，但是由于FLL带宽较大，达到锁定状态需要40ms到50ms，为了改善这一情况，文献[2]提出对解扩后的信号利用FFT来估计载波多普勒，由于FFT分辨率受到信号长度的限制，也不能取得很好的效果。例如，在5MHz的采样率下，1ms数据采样点为5000个，只能达到1kHz的分辨率，要达到100Hz的分辨率需要10ms数据，50000个采样点，这样不但计算量增大同时需要大的存储空间。文献[3]提出提高多普勒频率估计的分辨率的方法，将多普勒搜索单元设窄一些如250Hz、125Hz，但该方法会加大搜索空间，并且非常耗时。

本文在研究GPS信号特点的基础上，提出利用谐波恢复的ARMA建模法[4]对载波多普勒进行估计，仿真结果表明该方法可以得到非常稳定和精确的多普勒频率估计。高分辨率的多普勒估计不但可以缩短从捕获到稳定跟踪的时间，同时可将跟踪环路的带宽设计的较窄以达到较好的抗干扰的目的。

1 GPS信号模型

接收机接收到的信号模型为：

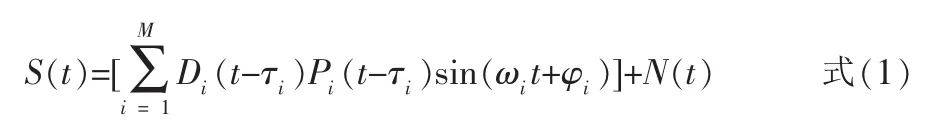
其中

M：可见卫星个数

Di：电文

Pi：伪随机码

ωi：GPS信号载波频率加多普勒频率

τi：信号延迟

φi：载波初始相位

N（t）：加性高斯白噪声

如果第j个信号被捕获，则解扩后的信号模型为：

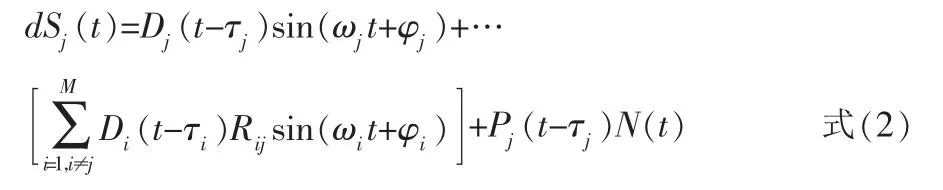
上式等号右边第二项中Rij为第j个伪随机码和第i个伪随机码的互相关，研究表明互相关部分最大可能功率为-21dB[5]，第三项为伪随机码和加性白噪声的相关。这两部分可以看作高斯白噪声，第一项为载波部分，其中载波相位φj是[-π，π]之间均匀分布的随机数。所以，解扩后的信号可以认为是平稳谐波过程与高斯白噪声的和，这样的观测信号，可以利用谐波恢复的ARMA建模法对载波的多普勒频率进行高分辨率的估计[6]。

当谐波信号在加性白噪声中被观测时，观测过程是一个特殊的随机过程，它的AR参数和MA参数完全相同，这一特殊的ARMA过程所服从的法方程为：

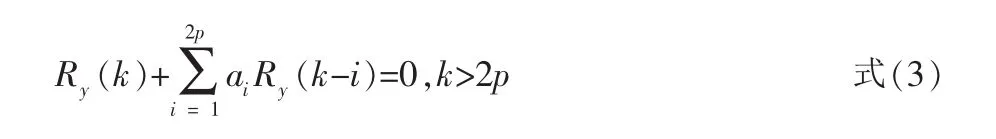
与修正的Yule-Walker方程类似，该方程可以构造超定的方程组，并使用SVD-TLS[6]算法求解。

具体算法：

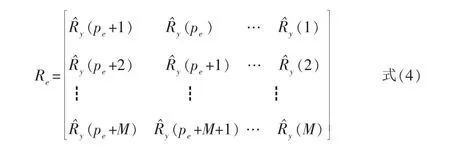
式中 pe＞2p，并且 M>>p；

步骤2 将矩阵Re当作增广矩阵，利用算法SVD-TLS确定AR的阶数2p和系数向量a的总体最小二乘估计；

步骤3 计算特征多项式

的共轭根 (zi，)，其中 i=1，…，p；

步骤 4 利用 fi＝arctan[Im（zi）/Re（zi）]/2π 计算载波的频率。

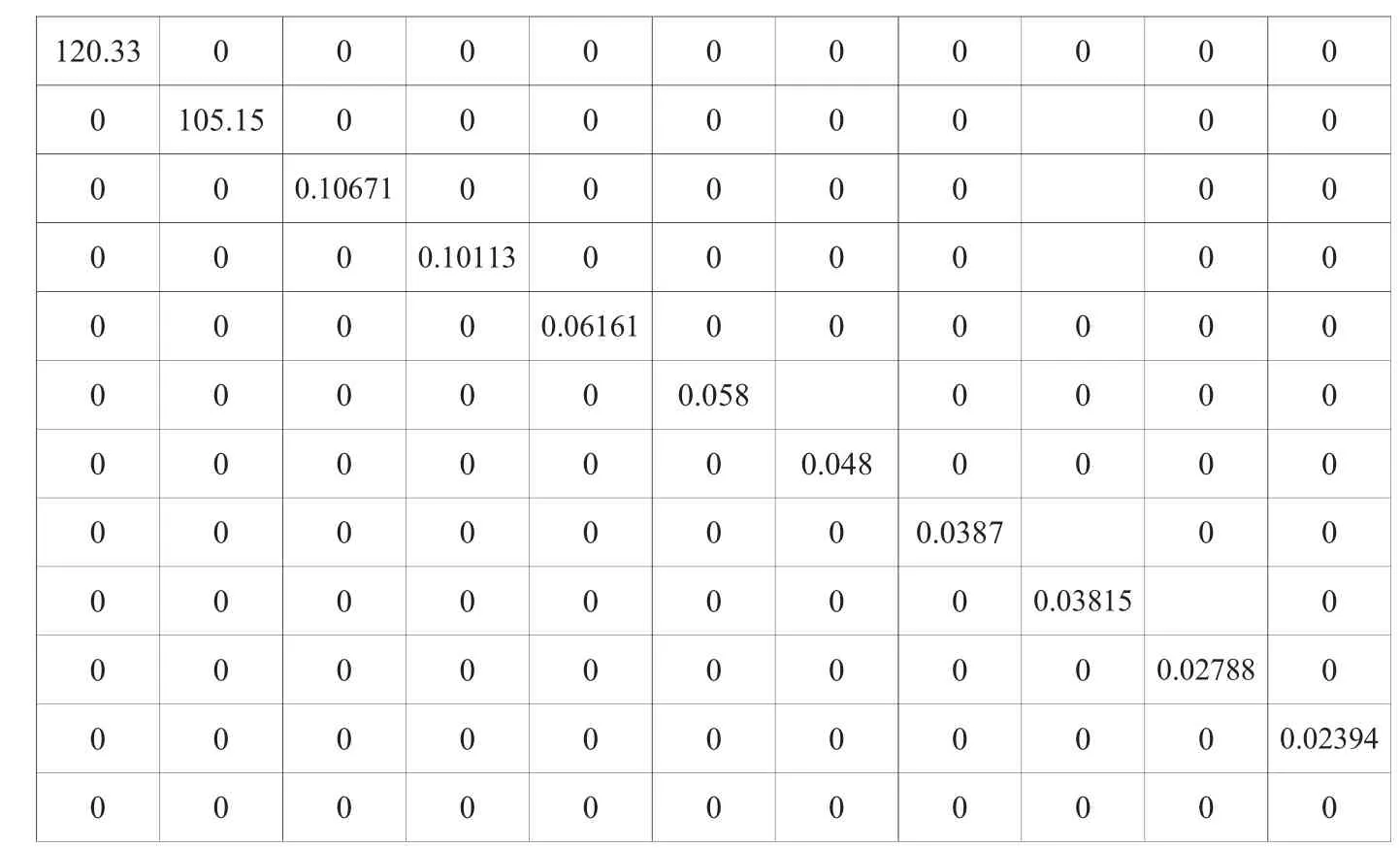
表1 本文采用的算法中奇异值分解特征值矩阵

2 谐波恢复的ARMA建模法

谐波恢复ARMA建模法由于使用了奇异值分解和总体最小二乘方法，整个计算具有好的数值稳定性，而且AR阶数和参数估计具有非常高的精确度。

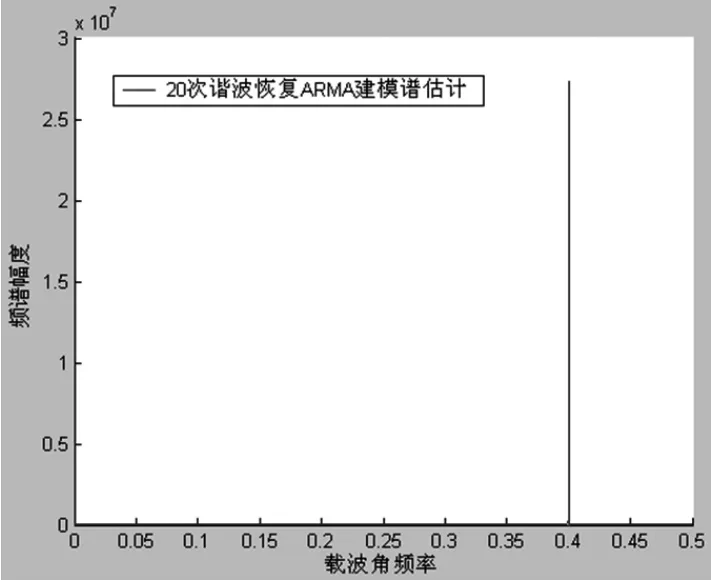
图1 本文方法估计载波多普勒仿真图

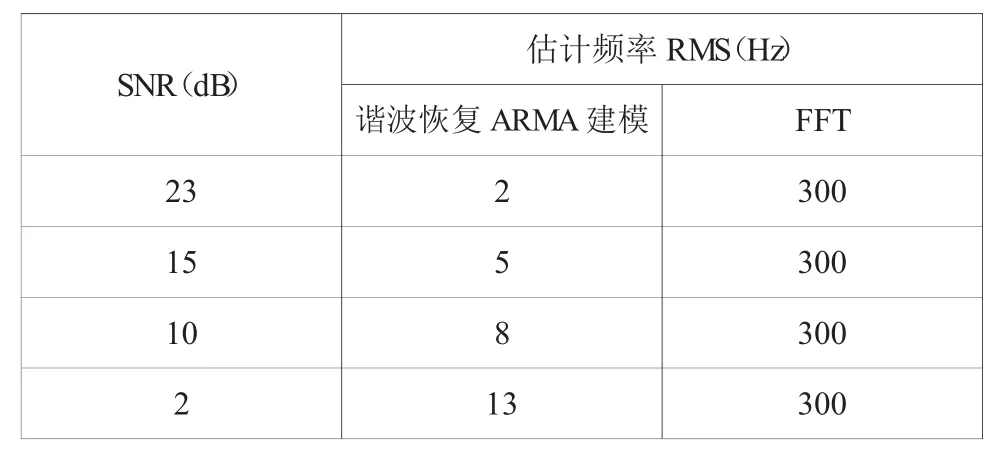
表2 频率估计RMS

3 仿真结果

本文利用MATLAB仿真，载波多普勒频率设为200.3kHz，仿真数据1ms，采样频率5MHz，由于估计的谐波频率只有 1个，所以 p=1，取 M=12，pe=10，当然也可以取其它值，只要满足扩展阶自相关矩阵的要求即可。表1为信噪比23dB时的奇异值分解特征矩阵，可以看出主要特征值2个，所以需要确定的AR阶数为2，谐波的个数即为1。

图1为20次仿真的谱估计图，可以看出每次的估计结果非常稳定，精确。

表2为仿真进行50次的频率均方误差和FFT的比较，由于FFT的频率分辨率对于1kHz的数据长度为1ms，其输出频率为1kHz的整数倍，所以其误差不随信噪比变化，为 300Hz。

另外，研究表明在MATLAB仿真环境下，对于1ms的积分时间，21个500Hz频率单元，需要125 e6次浮点运算，FLL若50ms达到稳定（频率牵引到20Hz内）需要40 e6次浮点运算，而本文采用的频谱估计方法学要20 e6次浮点运算，可见，采用高分辨率的载波多普勒估计可以大大减少从捕获到跟踪的时间。

4 结论

以上研究表明，对于解扩后的GPS信号，视为平稳随机过程和高斯白噪声的和，通过谐波恢复的ARMA模型法，对GPS多普勒进行高分辨率估计是完全可行的，可以取得非常满意的精度，以及稳定的结果，而且计算量也相对小得多，这对于减少GPS接收机从捕获到跟踪的时间，同时降低跟踪环路带宽以提高GPS接收机抗干扰能力是非常有意义的。

［1］Kaplan,E.Understanding GPS:Principles and Applications,Artech House,1996.

［2］Tsui,J.Fundamentals of Global Positioning System Receivers:A Software Approach.Wiley Inter-Science,2000.

［3］Lin,D.,Tsui,J.Comparison of Acquisition Methodes for Software GPS Receiver.Proceedings of ION:2385-2391,September,2000.

［4］Zhang X D,Takeda H.An approach to time series analysis and ARMA spectralestimation.IEEE Trans.Acoust.,Speech,Signal Processing,1987,35:1303-1313.

［5］Parkinson,B.,et al.(editors).Global Poisitioning System.Volume Ⅰ.American Institute of Astronautics and Aeronautics,1996.

［6］张贤达.现代信号处理[M].2版.北京:清华大学出版社,2003.