渐开线斜齿轮精确参数化建模关键问题研究

郭 利，陈 科

(1.安徽国防科技职业学院机械工程系，安徽 六安 237011;2.合肥工业大学机械与汽车工程学院，合肥 230009)

0 引言

利用优越的Pro/E软件对斜齿轮进行参数化实体建模，然后导入有限元分析软件ANSYS中进行应力应变等结构分析，是常用的斜齿轮优化设计手段之一。因此，对斜齿轮进行科学的分析和精确的参数化建模是十分关键的。通过仔细查阅关于利用Pro/E软件进行渐开线斜齿轮参数化建模的大量文献，如文献［1～6］，发现了几个被忽视的问题，使得渐开线斜齿轮精确参数化建模存在一定的不足，进而针对存在的几个问题提出了详细的解决办法。

1 精确参数化建模关键问题分析

1.1 基圆半径与齿根圆半径大小问题

由斜齿轮各参数关系式可知，齿轮齿数多少不同或齿轮正负变位的影响，都会造成齿根圆半径和基圆半径大小的不同，而齿根圆半径与基圆半径的大小直接关系到理论齿廓曲线的形状。如图1所示的齿廓曲线形状比较，a图中齿根圆半径小于基圆半径，理论齿廓曲线由渐开线和过渡曲线组成;b图中齿根圆半径大于基圆半径，理论齿廓曲线完全是始于基圆的渐开线;因此，在斜齿轮自动精确参数化建模过程中，必须考虑理论齿廓曲线的形状，否则，自动参数化建模会失败。

图1 齿廓曲线形状比较

program是Pro/E的二次开发工具之一，它用来记录模型创建的整个过程，并以一段带参数的简单程序来表示。通过修改程序，就可以方便地实现设计意图的变更与设计的自动化。因此，通过program的程序文件编辑功能来控制特征的生成与否和特征的个数及尺寸等操作来解决上述问题是可行的，添加的关系控制语句如下:

1.2 齿根过渡曲线问题

由上述分析可知，若齿根圆半径小于基圆半径，理论齿廓曲线由渐开线和过渡曲线组成。虽然齿轮工作时过渡曲线不参与啮合，但是过渡曲线却对齿轮根部的弯曲应力影响很大。所以，要进行精确地有限元分析，必须精确地绘制齿轮根部过渡曲线。

在齿轮实际生产中，由于采用的切齿加工刀具以及刀具齿顶圆弧形状不同，切出的齿根过渡曲线形状也不同，常见的有5种，不同加工工艺方法和刀具齿顶形状生成不同的过渡曲线，以刀具齿廓的顶部具有两个圆角的齿条型刀具加工齿轮为例，进行过渡曲线构造，图2为齿条型刀具齿廓简图。

图2 齿条型刀具齿廓简图

如图2所示，ρ为刀顶圆角半径，O为圆心，h为齿顶高系数，c为顶隙系数，m为齿轮模数，刀顶圆角圆心O距中线的距离设为a;刀顶圆角圆心O距刀具齿槽中心线的距离设为b。由参数关系可知:

用上述刀具加工齿轮生成的过渡曲线为延伸的渐开线等距曲线，如图3所示。

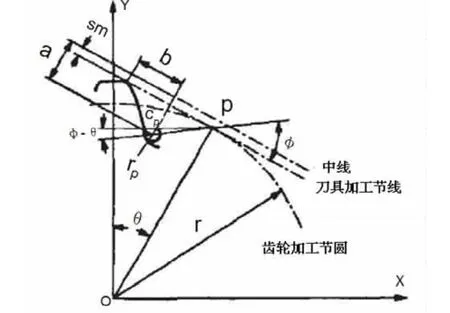
图3 延伸渐开线等距曲线简图

其过渡曲线参数方程如下:

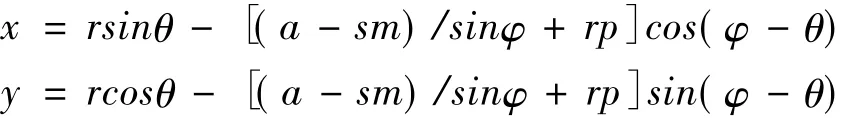
式中 θ= ［(a+sm)cotφ +b］/r，s为变位系数，φ角是变参数，在0～90°范围内变化。按照渐开线方程生成渐开线，按照上述参数方程生成齿根过渡曲线，如图4所示。

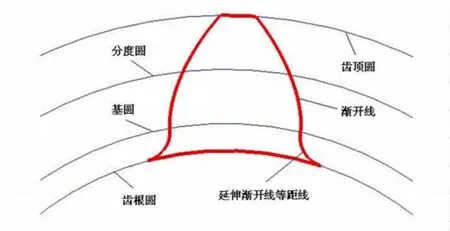
图4 齿廓曲线的实际形状

1.3 螺旋轨迹线问题

在斜齿轮建模时，需要绘制螺旋轨迹线。许多文献和教程用投影法得到螺旋轨迹线。经分析，这种方法实现的螺旋轨迹线是存在误差的，而且，螺旋角越大，其误差也越大。因此，斜齿轮建模也不够精确。

斜齿轮的螺旋线的变化是较复杂的，随着齿厚、压力角等参数的变化而不同。图5所示是由分度圆柱展开面剖切得到的螺旋轨迹线OP。图中，d为分度圆直径，L为螺旋线的导程，β为螺旋角，b为齿宽。由几何关系推导可知，螺旋轨迹线OP的方程如下:

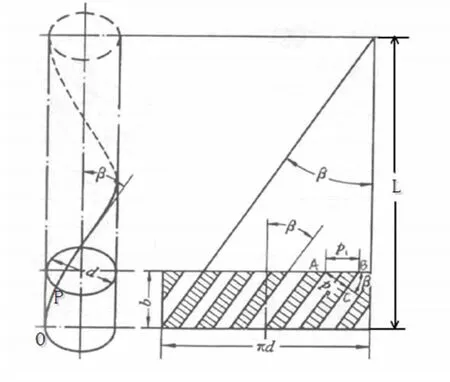
图5 在分度圆上的螺旋线展开图

其中，t是Pro/E中方程控制变量参数，在0～l之间变化。由上述参数方程生成的螺旋轨迹线才是最精确的螺旋线，建模时应当由参数方程驱动创建螺旋轨迹线。

2 结束语

渐开线斜齿轮精确参数化建模是导入ANSYS有限元分析软件进行各种结构分析的基础。通过对斜齿轮精确参数化建模中容易忽视的三大关键问题进行分析和研究，并给出解决方法，能更好地满足实际工程分析和优化设计的需要。

［1］刁立峰，黄阳，代明.基于Pro/E二次开发技术的齿轮参数化造型［J］.机电产品开发与创新，2006(5):88－89.

［2］张文丽.VB二次开发Pro/ENGINEER建立齿轮参数化模型系统［J］.机械传动，2010，34(9):50－52.

［3］罗善暖，王建.渐开线斜齿轮的参数化建模方法与虚拟装配技术［J］.机械传动，2006(19):26－27.

［4］幸保，高英武，汤楚宙.齿轮的参数化设计与三维建模的方法研究［J］.机械设计与制造，2010(8):30－32.

［5］贾吉林.基于Pro/E斜齿圆柱齿轮参数化设计及运动仿真［J］.煤矿机械，2010，31(7):230－232.

［6］张海军，张广川，任乃飞.Pro/E WildfIRE3.0中标准渐开线斜齿圆柱齿轮参数化设计［J］.现代制造工程，2007(4):97－99.

［7］吴继泽，王统.齿根过渡曲线与齿根应力［M］.北京:国防工业出版社，1989.

［8］贺云花.斜齿轮强度的三维参数化有限元分析［D］.济南:山东大学，2007.