基于ARIMA模型的全球跨国快递业务量预测
2012-07-05张仲斐赵一飞
张仲斐,赵一飞
(1.上海交通大学中美物流研究院,上海200030;2.上海交通大学安泰经济与管理学院,上海200030)
快递也称之为速递,是交通运输行业中的新兴子行业,通常国际上将快递市场定义为CEP(Courier,Express and Parcel)市场,是指快递公司通过铁路、公路、海运和空运等方式,对客户的货物进行投递。目前全球性快递公司主要有UPS(联合包裹服务公司)、FedEx(联邦快递)、DHL和TNT快递,这四家被称之为全球快递行业的四巨头。
在国际快递公司提供的服务产品中,跨国快递是最高效快捷和最高端的产品。跨国快递(transnational express)通常是指收件地和派件地分处两个国家,采取空运方式派送的快件。进入这一市场需要有较大的网络规模和较强的运营能力,形成了其特殊的进入壁垒,因此目前在这一市场上处于多寡头垄断局面,上述四家占据全球跨国快递产品市场上约80%的市场份额。自从上世纪80年代出现跨国快递以来,该项业务发展迅猛,全球跨国快递业务量具有周期趋势和季节波动趋势。如果能够准确预测未来一段时间的业务量,将会为我国快递企业进入国际市场提供指导意见,在国际竞争中占据一席之地。
我国学者对于国际快递的研究,主要局限于快递企业的发展和战略上,王增樑(2008)[1]对国际快递业的发展进行了分析,方琳和王迎军(2008)[2]研究了国际快递的品牌优势,苏旻昱和赵一飞(2008)[3]分析了工业工程技术在国外以快递为代表的物流行业中的应用,不过国内尚未有针对跨国快递业务量做预测的研究。
为了填补这一块研究的空白,本文试图从动态角度观察跨国快递业务量,利用对其历史数据的分析得到其规律性,并用以预测其未来值。考虑到跨国快递业务需求量序列为非平稳时间序列,而传统的时间序列模型只能描述平稳时间序列的变化规律,因此选择统计学家Box和Jenkins[4-5]提出的ARIMA模型(autoregressive integrated moving average model),又被称为B-J模型,用于非平稳时间序列预测。
ARIMA模型中使用自回归项(AR项)、单整项(I项)和移动平均项(MA项)3种形式对扰动项进行建模分析,使模型同时综合考虑了预测变量的过去值、当前值和误差值,从而有效地提高了模型的预测精度。因此,最终选择ARIMA模型对全球跨国快递业务量进行分析和预测。
1ARIMA模型和建模步骤
1.1 平稳时间序列ARIMA模型
所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程[6]。
自回归模型AR(p)满足下面的方程

其中:参数c为常数;ϕ1,ϕ2,…,ϕp是自回归模型系数;p为自回归模型阶数;εt是均值为0,方差为σ2的白噪声序列;T为系数最大项。
移动平均模型MA(q)满足下面的方程

其中:参数μ为常数;θ1,θ2,…,θp是q阶移动平均模型的系数;εt是均值为0,方差为σ2的白噪声序列。
ARMA(p,q)模型
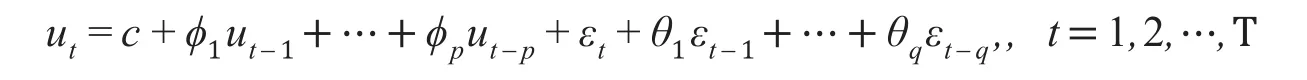
实质上是自回归模型AR(p)和移动平均模型MA(q)的组合形式,称为混合模型,常记做AMRA(p,q)。
而ARIMA(p,d,q)模型,既ARMA(p,q)模型加上I,I为差分,d为使时间序列成为平稳时间序列的差分次数。
1.2 ARIMA模型的建立步骤
1)模型的平稳性检验。在对经济时间序列进行分析前,可以考虑对原始序列做对数处理,消除异方差。然后对对数序列进行检验,通常是采用ADF单位根检验法,根据ADF检验值,若其大于单位根检验的临界值,则认定该时间序列为非平稳时间序列,需要对其进行差分处理,直至得到一个平稳的序列。对于经济时间序列,差分次数d通常只取0,l或2。
2)模型参数的识别。根据时间序列模型的识别规则,建立相应的模型,若平稳的时间序列的自相关函数和偏自相关函数都是拖尾,则此序列适合ARIMA(p,d,q)模型。通过序列的自相关函数、偏相关函数表现的特征,进行初步的模型识别,并且坚持保守原则,尽量选择小的(p,q),并根据AIC准则验证完成最终参数的确定。
3)模型诊断和检验。模型诊断与检验有两个方法:一是根据模型的残差序列是否为白噪声序列来判断模型是否为适应性模型;二是通过计算ARIMA(p,d,q)模型的特征根来检验其平衡性,通过AIC信息值和SC信息值等进行判断。
4)预测和评价。运用确定的ARIMA(p,d,q)模型对数据进行预测。首先预测出样本时间区间末尾的数据,并和原始序列对比得出预测误差,如果预测误差较小,表示可以考虑接受该模型,并运用该模型对未来的数据进行预测。
2 全球跨国快递业务量建模实例研究
本文使用Eviews5.1对数据序列进行处理和预测[7]。
本文所采用的全球跨国快递业务量的季度数据的样本区间为2001年第1季度至2010年第4季度。数据来源为四大快递公司的季度跨国快递包裹量总和,单位为千件/每天。之所以采取四大公司的跨国快递包裹量作为研究数据序列,是因为其占据全球跨国快递市场上约80%的市场份额,认为其可以代表跨国快递的业务量。
经过原始数据处理后,设原序列为Xt,其中t=1,2,…,T
从图1中可以看出,原序列有明显的增长趋势,并带有强烈的季节特性,对原始序列进行ADF检验结果如表1所示。

图1 原序列Xt线性图Fig.1 Line graph of primitive sequenceXt
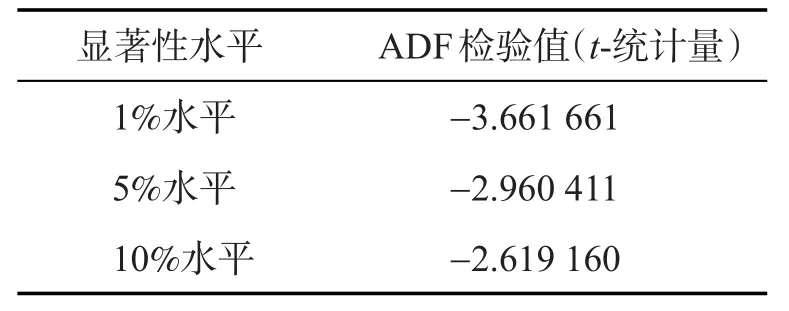
表1 原始序列ADF检验Tab.1 ADF test of primitive sequences
可见,ADF检验统计量为-1.649,显然大于10%显著水平的临界值,说明原时间序列是非稳定的。因此要对原序列进行对数和差分处理。经过处理后的序列如下

如上面的式子所示,{Yt}是对{Xt}取对数所得到的系列;{Zt}为{Yt}的一阶差分;{St}是对{Zt}进行季节差分,以消除季节因素的影响。最终3个序列的ADF检验结果如表2所示。
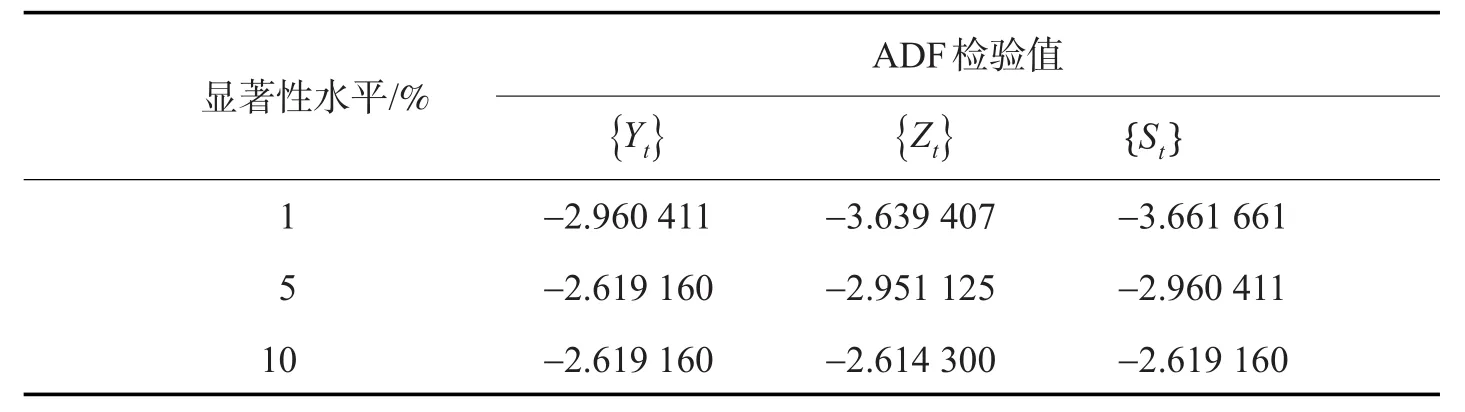
表2 处理后序列ADF检验结果Tab.2 ADF test results of processed sequence
序列{St}的ADF检验统计量为-5.335 464,小于1%显著性水平,因而在99%置信水平下通过ADF单位根检验,为平稳时间序列。因此在ARIMA模型中,参数d设置为1。
通过图2可以清楚看到,经过取对数、一阶差分和季节差分的处理之后,序列{St}的增长趋势已经基本被消除,季节性变动的因素也已经消除,基本符合平稳时间序列的性质。
从St自相关函数图和偏相关函数图我们可以看到,他们都是拖尾的,因此可以设定为ARMA过程。St的自相关函数前4阶都是较为显著的,从第5阶开始表现不明显,不过第2,3,4阶表现得并非十分显著,因此q可以考虑取1或者4。

表3 各模型检验结果Tab.3 Test results of each model

图2 序列St线性图Fig.2 Line graph of sequenceSt
St的偏相关函数第1阶和第5阶表现显著,因此p可以考虑1或者5。
根据模型检验结果,模型(1,1,1)的AIC和SC检验参数最为理想,因此最终确定模型为ARIMA(1,1,1)(1,1,1)4,原序列名称为volume,在EVIEW中按下式建模:

其中:sar(4)和sma(4)分别表示季节自回归部分和季节移动平均部分的变量。
根据序列{St}的模型,对其进行回归拟合,得到相应的拟合值和残插图。从图3中可以看出模型拟合得较为理想,实际值和拟合值的较为一致。

图3 序列St自相关函数图和偏相关函数图Fig.3 Autocorrelation and partial correlation graph of sequenceSt

图4 拟合实际值对比图Fig.4 Comparison graph of actual and fitted value
同时观察残差序列(见图4),相对平稳,没有明显的趋势性,可以判断残差为白噪声过程,整个模型的拟合效果较好。
该模型的参数检验结果如表4,检验参数AIC信息值为-4.207 959,SC信息值为-4.021 133,均较小表明模型较优,通过检验。
因此最终可以选择ARIMA(1,1,1)(1,1,1)4作为模型,根据该模型进行预测和结果对比。
模型检验参数结果如表5,检验参数AIC信息值为-4.207 959,SC信息值为-4.021 133,均较小表明模型较优,通过检验。因此最终可以选择ARIMA(1,1,1)(1,1,1)4作为模型,根据该模型进行预测和结果对比。
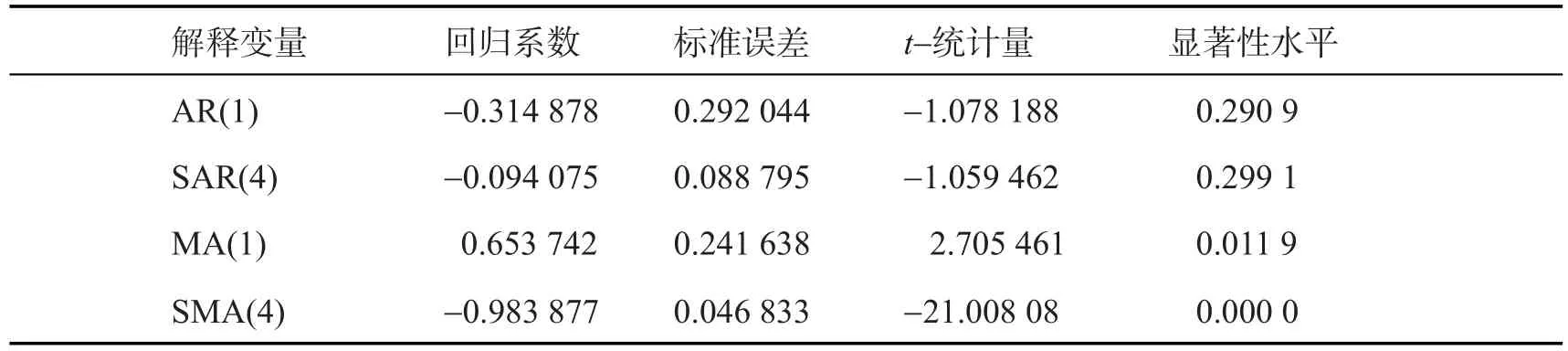
表4 ARIMA(1,1,1)模型的估计结果Tab.4 Estimation ofARIMA(1,1,1)

表5 ARIMA(1,1,1)模型的估计结果Tab.5 Estimation and results ofARIMA(1,1,1)
3 预测结果与结论
因此,根据dynamic预测方式对序列末尾(时间区间:2010年第1季度至2011年第2季度)进行预测,并将得到的预测值与原始序列实际值做对比,结果参见表6。

表6 实际数据与预测数据比较Tab.6 Comparison of actual data and forecasting data
观察ARIMA模型的短期预测结果,发现效果良好。从表4后两行可以看出,预测值与实际值的差异较小,说明模型预测的效果良好。由预测值对实际值的偏离除以实际值,得到误差的相对比例,在0.99%~6.87%之间波动,6期数据平均误差在3.96%。
上述对2010年第1季度至2011年第2季度的预测结果对比表示,因此,ARIMA(1,1,1)(1,1,1)4模型可以用于对于国际快递业务需求量的预测。

图5 残差序列图Fig.5 Graph of residual sequences

图6 预测业务量走势图Fig.6 Chart of forecasting business volume
ARIMA模型在短期内预测比较准确,随着预测的延长,预测误差会逐渐增大,这是ARIMA模型的缺陷。但是与其他的预测方法相比,其预测的准确度还是比较高的,尤其在短期预测方面。并且模型在经过加入季节变量调整之后,对于季节趋势的预测表现得更为优秀,能够为公司制定战略和发展方向提供参考。
因此用该模型对未来两年的数据做预测,结果如表7。
为了反映预测模型对序列整体趋势的描述,将原始序列实际值和预测值合并到一张图上,见图6。
根据模型的预测,对季节趋势的判断还是较令人满意的,基本符合之前历史序列中,每年第4季度出现旺季小高峰的趋势。在长期趋势方面,未来两年之内的全球跨国快递业务量仍将保持高速增长,并在2013年4季度达到2 082.95千件·d-1的高峰,在度过2008至2009的全球金融危机之后,又将迎来一波新的业务量增长。

表7 对未来全球跨国快递业务量预测值Tab.7 Forecasting value of future global transnational express volume
[1]王增樑.国际快递业发展现状分析及对策[J].中国高新技术企业,2008(6):13-18.
[2]方琳,王迎军.国际快递企业的品牌优势分析及启示——护佑理论的视角[J].物流技术,2008,27(8):236-238.
[3]苏旻昱,赵一飞.工业工程在我国物流行业中的应用[J].物流科技,2008,31(4):91-94.
[4]BOX G,JENKINS G.Time series analysis,forecasting,and control[M].San Francisco:Holden Day Press,1970:1-15.
[5]BOX G,JENKINS G,MACGREGOR J.Some recent advances in forecasting and control,part two[J].Statist,1974(4):158-179.
[6]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2006:126-168.
[7]易丹辉.数据分析与Eviews应用数据[M].北京:中国统计出版社,2002:106-134.
[8]靳庭良.计量经济学[M].成都:西南财经大学出版社,2011:20-38.
