基于多孔介质理论的冻土水热迁移耦合模型推导
2012-07-04李杨
李 杨
(1.福建工程学院 土木工程系福建 福州350014;2.吉林大学建设工程学院吉林长春130026)
土体是一种多孔介质,土体中水分的迁移流动属于多孔介质流体流动[1-2]。1957 年,Philip和de Vries基于多孔介质中液态水粘性流动及热平衡原理,提出了水热耦合迁移模型,开创了土中水热耦合研究的先河[3]。作为一种特殊的土体,非饱和冻土的固相由固体颗粒和冰共同组成,Aboustit[4],Gatmiri等[5]相继对冻土中水热迁移耦合模型进行了研究。国内对冻土水热耦合迁移问题的研究起步较晚,当前主要集中在研究正冻土尤其是饱和正冻土中水热迁移问题等方面[6],而对非饱和季节冻土的水热迁移耦合问题的研究目前仍存在一些不足,如不能很好的模拟自然界边界条件、水分迁移的机制不确定及水分迁移过程的数值模拟与模型计算过于简单等。本文利用质量平衡原理、能量平衡原理、热工原理,考虑温度变化过程中冻土中水分相变和温度、质量变化之间的相互影响,同时考虑扩散和对流,建立了非饱和冻土系统水分迁移和热量迁移的耦合数学模型。
1 建模基本假设和基础理论
1.1 建模基本假设
(1)土体为非饱和土,冻融过程中土体孔隙中水分迁移存在多种状态。冻前:液态水、气态水;冻结或融化过程:液态水、气态水、固态冰;融化后:液态水、气态水。
(2)假设孔隙中水的相变在一次温度变化过程中存在单向非可逆性。
(3)假设水分迁移过程中无溶质迁移。
(4)假设水分迁移符合非线性达西定律。(5)假设土体各向同性。
1.2 基础理论
非饱和土体由固相、液相和气相三相组成,冻结过程中存在水、汽、冰共存的状态。为了更好地模拟土体冻结过程,本模型同时考虑了水的相变以及体系中液态水、气态水、固态水(冰)、土体密度、温度及变形速度之间的耦合情况。土体冻结过程中将发生水分的迁移,水分迁移存在两种方式:扩散迁移和对流迁移。扩散迁移包括扩散传质和扩散传热,其动力是温度差ΔΤ、浓度差Δu;对流迁移包括对流传质和对流传热,其动力是土水势差Δψ。部分土体冻结过程中将发生冻胀,使土颗粒发生位移,孔隙体积发生变化,从而导致土体密度发生变化。
2 水分迁移方程
2.1 达西流动方程
水分迁移的最基本方程即为达西流动方程。本文即以最基本的达西流动方程为基础,推导出无相变的水分迁移方程以及考虑相变的水分迁移方程。
从土中取出微小土体单元Δn,设单元体的边长分别为Δx,Δy,Δz(图 1),则达西流动方程可表示如下:

式中:ωjx,ωjy,ωjz(j=l,g)- 液态水、气态水在x,y,z三个方向的迁移速度;Kωjx,KωjY,KωjZ(j=l,g)-土体中液态水、气态水在x,y,z三个方向渗透系数;μj(j=l,g)-土体中液态水、气态水迁移时所受的粘阻力。
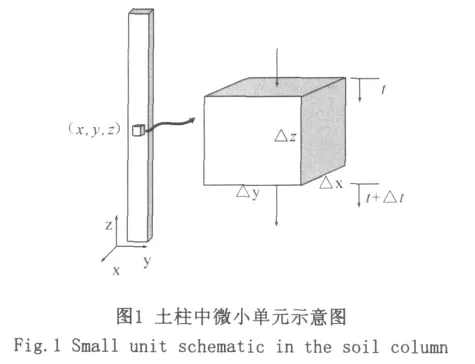
由于冰质量的变化仅是来于相变,并没有外界的流入,所以冰流动速度ωjx=ωiy-ωiz=0。
2.2 无相变的水分迁移方程
如前所述,在Δt时间内经各方向流入单元体的液态水的速度为ω,单位时间流入单元体积的液态水质量通量相等,假设不考虑相变和土颗粒的位移,则各界面的面孔隙比相等且不变,根据一级近似,可有:

式中:θj-土中各水分相的质量百分含量;e-孔隙比;ρd-土粒干密度;Dj-各水分相扩散系数;Lsj-各水分相soret效应系数;ρs-土粒密度;ρj-土中各水分相的质量密度,ρj=ρsθj;Tj-各水分相温度。
则结合式(1)、式(2)可得无相变时的液态水、气态水迁移方程
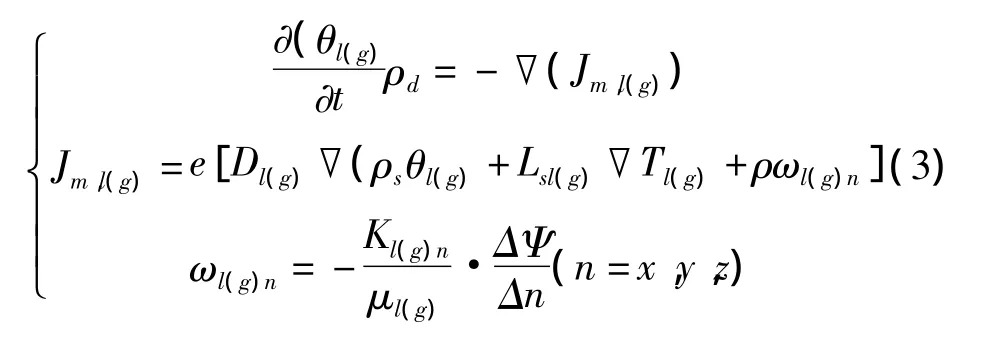
2.3 考虑相变的水分迁移方程
相变本身由温度产生,但质量的传递也会影响温度传递,所以综合来看相变是由质量梯度和温度梯度共同决定[7]。平衡状态下有 Γg,l= -Γl,g,Γl,g为液态水蒸发变化量,Γg,l为水汽凝结变化量;Γl,i= - Γi,l,Γi,l为冰融解变化量,Γl,i为液态水冻结变化量;Γg,i= - Γi,g,Γi,g为冰升华变化量,Γg,i为水汽凝华变化量。
记总含水率为
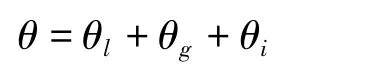
式中:θl,θg,θi- 液态含水率,气态含水率以及含冰率。
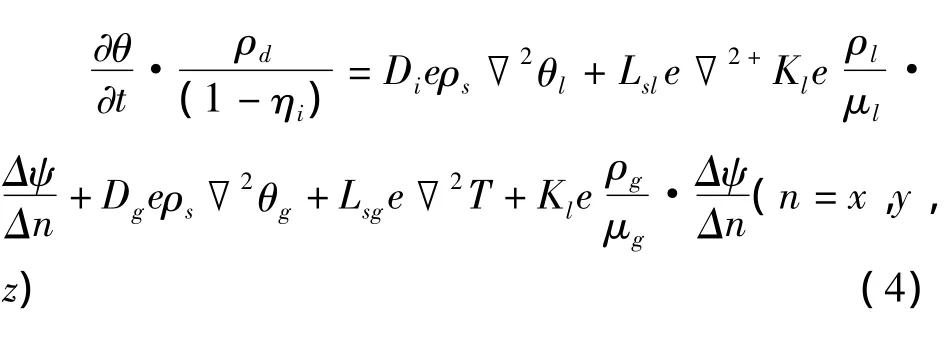
2.4 土体传热过程
土体冻结过程中土体中热量亦产生传递变化[8],因此根据能量守恒定律,系统热量的变化是由密度梯度和温度梯度引起的导热量的变化、渗透作用引起的热量对流产生的热量变化和相变引起的热量变化共同决定。土体传热方程见式(5)。
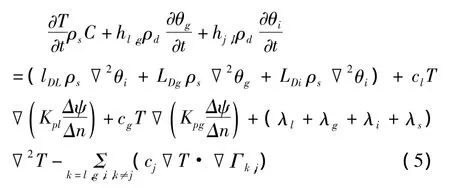
2.5 骨架质量密度变化方程
1骨架质量密度变化方程
根据孔隙比定义可得

式中:ωs-骨架变形速度。
2骨架传热方程
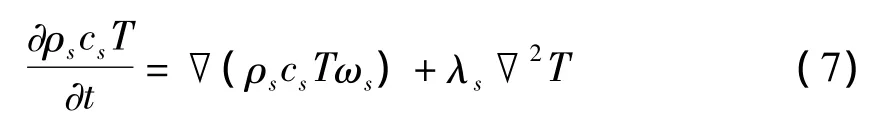
式中:Cs-骨架热容;λs-骨架导热系数。
3骨架变形速度方程
在水分迁移过程中,部分孔隙被外界水补充,部分液态水会相变成冰,使孔隙体积发生变化。假设Δt时间内,流进骨架孔隙的水分别变成为液态水、气态水和冰,则骨架变形速度为
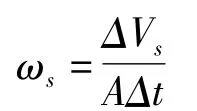
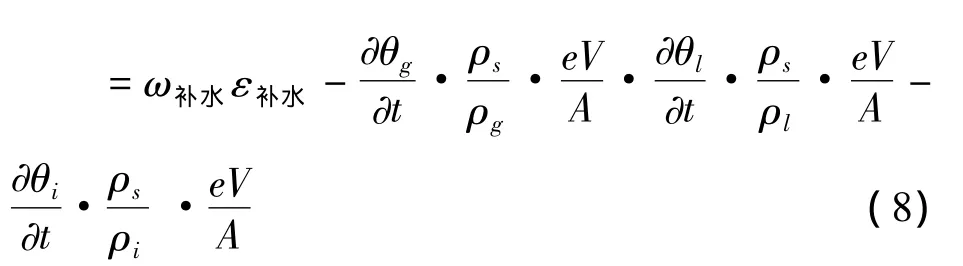
式中:ε补水-面孔隙率(比);e-体孔隙比;V-土柱体积;A-土柱截面面积。
2.6 水热迁移耦合模型
式(4 -8)中,未知变量为θl,θg,θi,ρg,ρs,ωs,合计6个。引入未冻含水率与温度的关系

至此方程达到6个,模型可解。该模型方程属于非线性偏微分方程,无法得出解析解,必须采用数值解法。
3 其他模型参数的确定
3.1 分子质量扩散系数
(1)液态水的扩散系数 Dl,根据实验结果拟合。

式中:Dg-土中空气质量传导常数;Mg-空气分子质量;R-气体常数;T-绝对温度;Sr-土的饱和度。
3.2 Soret效应系数(Lsl,Lsg)和 Dufour效应系数(LDl,LDg)
由于温度梯度ΔT存在,打破了Fick系统质量分布平衡,称之为Soret效应,则Soret效应系数
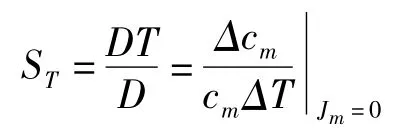
由于密度梯度ΔCm的存在,打破了傅立叶系统热量分布平衡,即 Dufour效应,则 Dufour效应系数
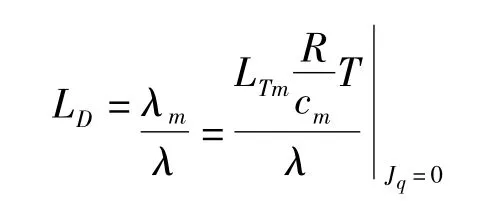
3.3 质量渗透系数
(1)液态水的质量渗透系数Kpl。

式中:e-土的孔隙比;μ-水的动力粘滞系数,Pa·s;ρl-水的密度,g/cm3;C-与土的颗粒形状等有关的系数;Ss-土颗粒的比表面积,cm-1。
(2)水汽的质量渗透系数Kpg。

3.4 运动粘度系数
液态水和气体的运动粘度系数μl与温度有关,经过拟合得
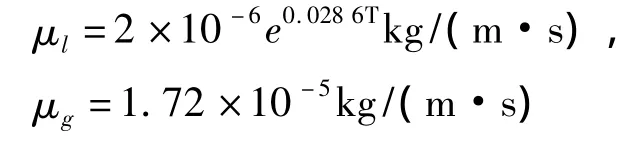
3.5 导热系数
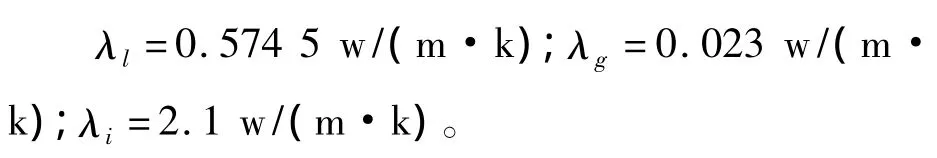
土体的导热系数λs根据实测的数据由拟合得出。
3.6 比热
水的比热cl(15℃)=1.002 J/(kg·℃);水汽定压比热cg=0.445 J/(kg·℃);冰的比热 ci=0.505J/(kg·℃);土的比热根据实际土样测量得到。
3.7 相变比焓
水的蒸发(或水汽凝结)潜热 Lg=597.4×4.186×1 000 J/kg;水的冻结(或冰融解)潜热Lf=79.72 ×4.186 ×1 000 J/kg;冰升华(或水汽凝华)潜热 Ls=677.12×4.186 ×1 000 J/kg。
3.8 各相体积比
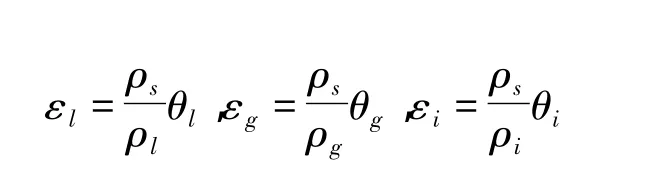
3.9 密度
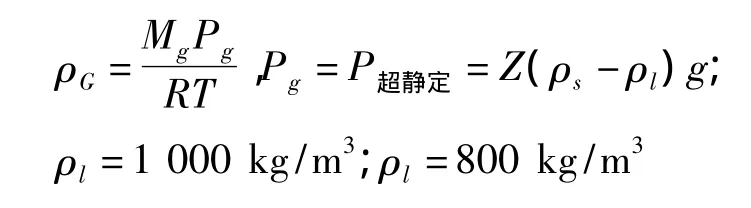
4 结语
本文以多孔介质理论为基础,建立了非饱和土冻土系统水分迁移和热量迁移的耦合数学模型,同时给出了模型参数的确定方法,通过对模型求解(数值法),即可求得非饱和土体冻结过程中温度、含水率(包括未动含水率,总含水率)的迁移变化过程。模型中不仅考虑了冻土温度变化过程中水分相变和温度、质量变化之间的相互影响,同时亦考虑了扩散和对流,因此模型可以较好地模拟自然边界条件,使模型的计算结果更加接近实际情况。其结果可为研究实际土体的水分迁移过程提供理论参考,并可为季冻区防治冻胀提供理论指导。
[1]陈飞熊,李宁,徐 彬.非饱和正冻土的三场耦合理论框架[J].力学学报,2005,37(2):204-214.
[2] BEAR J,BECHMAT Y.Introduction to modeling of transport phenomena in porous media[M].Netherlands:Kluwer Academic Publishers,1991.
[3]PHILIP J R,DE VERIES D A.Moisture movement in porous material under temperature gradient[J].Trans Am Geophys Union,1957,38:222-232.
[4]ABOUSTIT B L,ADVANI S H,LEE J K,et al.Finite element evaluation of thermo-elastic consolidation[C]//Society of Mining Engineers of AIME.Proceedings US Symp Rock Mech.Berkeley,California:American Rock Mechanics Association,1982:587-595.
[5]FREMOND M,MIKKOLA M.Thermo-mechanical of freezing soil[C]//Black P B.Proceedings of the sixth International Symposium on Ground Freezing.Rottendam,Netherlands:A.A.Balkema,1991:17-24.
[6]陈飞熊,李宁,程国栋.饱和正冻土多孔多相介质的理论构架[J].岩土工程学报,2002,24(2):213-217
[7]叶尔绍夫.工程冻土学[M].莫斯科:莫斯科国立大学出版社,1999.
[8]赵进,王景刚,杜梅霞,等.地源热泵土壤热物性测试与分析[J].河北工程大学学报:自然科学版,2010,27(1):45-48.
[9]卢廷浩.高等土力学[M].北京:机械工业出版社,2006.
