双目标纯方位定位数据处理分析
2012-07-04唐扬刘承禹胡科强
唐扬 刘承禹 胡科强
(1. 海军工程大学兵器工程系,武汉430033;2. 二炮研究院,北京100085)
0 引言
单个矢量水听器无法直接测得水下目标的距离增加了量测的不确定性[1~4],失去观测站本身所具有的定位跟踪能力。不借助其他传感器,观测站只能转换到被动。被动工作方式所获得的定位跟踪目标的定位精度,要低于没有干扰的情况。测角误差对定位跟踪精度的影响一般要大于测距误差,所以研究有效的被动传感器定位跟踪数据关联算法具有较高的理论价值和现实意义。
本文利用时空关联迭代找到目标同一时刻散射的水声信号在两方位序列中的位置,采用航真状态转移和平滑窗相结合以减小数据波动和实现航真管理实现双目标的有效跟踪,并对跟踪性能进行了仿真实验。
1 纯方位定位解算原理

P的坐标为:

考察两个浮标的关联问题,浮标i保留原方位序列,即根据真真真值点的直角坐标,直接换算成该浮标的方位数据。取k时刻及k+1时刻的真真真值点,作线性插值,可产生浮标 j的方位序列,需确定相对延迟点数Δk及时延修正量δi:

式中: R ound[·]表示四舍五入,c为声速,T为数据采样率。于是, β2(k +Δk )与β1(k)建立了基本的时空关联。其次,对该式[·]内的量值取小数部分,赋予δi,再基于k时刻真真真值点坐标,以v⋅ T⋅δi(v为目标航速)步长向k+1时刻真值点方向插值,换算成方位数据,添入 β2(k + Δk )即可。若 δi>0.5,则上述过程中的δi以1-δi代之,且基于 k +1时刻真真点向k时刻真真点反向插值。至此,生成了用于仿真的方位数据序列。此时,若利用同时刻的β1(k)与β2(k)进行跟踪,将产生偏量,称做无关联解算。实际解算,需利用文献[6]的迭代算法进行关联。

图1 双基阵纯方位定位解算原理图
2 卡尔曼滤波器用于纯方位TMA
卡尔曼滤波的基本出发点是建立恰当的数学模型,即描述动态过程的状态方程和量测方程。
取状态矢量为:
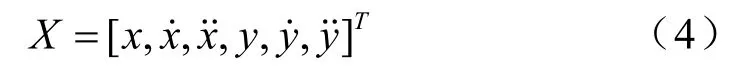
观测矢量为:

则相应的状态方程和测量方程分别为:
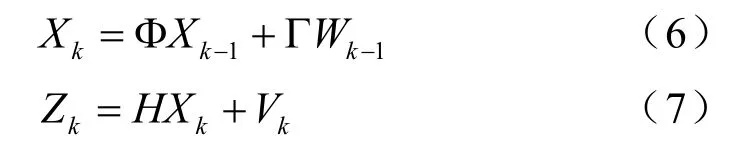
其中,Φ是状态转移矩阵,Γ是随机扰动加速度状态转移矩阵,H是测量矩阵,它们分别满足:

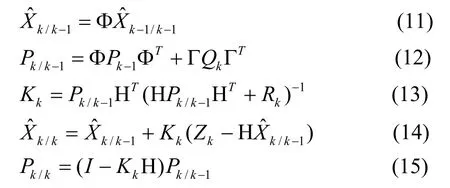
采用三点法得到初值,用限定下限法抑制滤波器发散[7]。
3 航真状态转移处理
利用门限鉴别法判别“野值”,即每个测量点真都与滤波器的预测点真进行比较,若其间距超过预设门限 D(取值与上节所述相同),则暂定为“野值”,作为试探航真 A[8]的初值加以保留,而滤波器仍以预测值代替测量值继续进行处理,在处理中使用三阶非线性拟合套以 26点滑动时间窗,然后进行卡尔曼滤波处理。如图2。
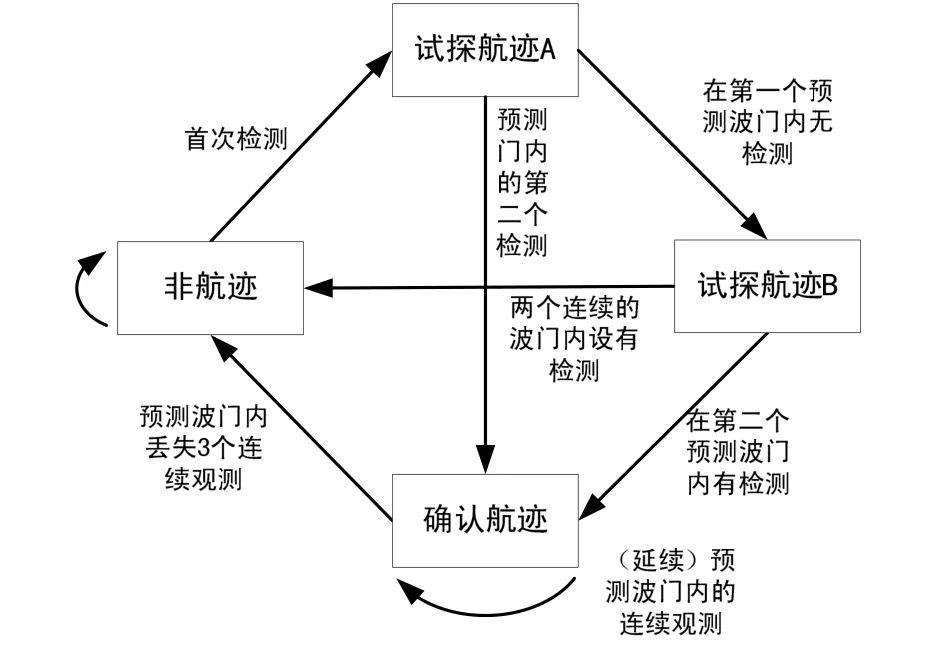
图2 航真状态转移图
基于航真状态转移的目标跟踪处理软件流程如图3所示。

图3 程序流程图
4 仿真实验与分析
我们对上面分析的双基阵纯方位 TMA方法进行了仿真计算。图4给出的是数据关联前后,卡尔曼滤波仿真的结果,图5、6给出了两种情况下的距离误差比较。从图可以看出,双基阵纯方位 TMA的目标估计是收敛的,且数据无关联解算表现为有偏测量,其解算结果与真实情况相比产生了很大的偏量,而数据关联后则基本消除了两浮标的时空差异所带来的影响。

图4 真真跟踪

图5 目标1误差比较图
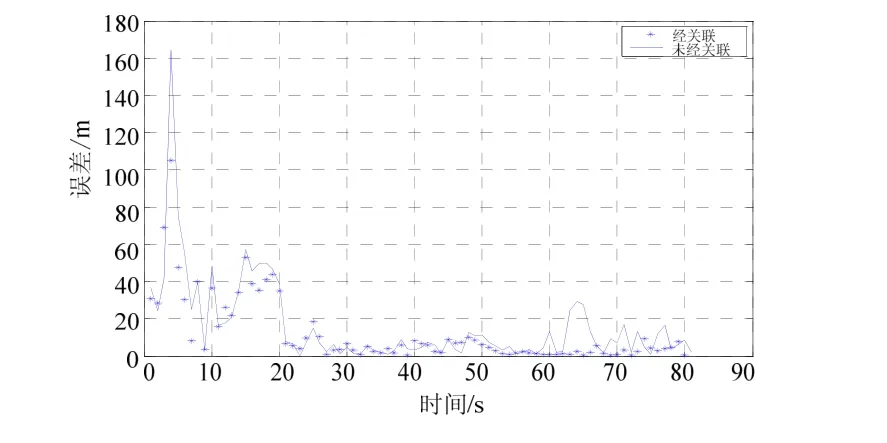
图6 目标2误差比较图
5 结论
本文对双基阵纯方位定位中数据时空校准,航真状态转移和航真管理进行了研究,分析了数据关联、航真状态转移、平滑滤波对卡尔曼滤波和实时目标跟踪的影响效果。通过仿真实验,数据关联有效消除了两浮标的时空差异所带来的影响,提高了算法的稳定性和全局收敛性;通过航真状态转移进行航真管理实现双目标的实时跟踪处理。
[1]MR. Garey and D.S .Johnson, Computer sand Intract ability: A Guide to the Theory of N-P Completeness.SanFrancisco, CA: Freeman,1979.
[2]C.H.Papa dimitriouand K. Steiglitz, Combinatorial Optimization: Algorithms and Complexity E nglewood Cliffs, N J:P rentice-Hall,1982 .
[3]Ljung L. Asymptotic behavior of extended kalman filter as a parrameter estimator for linear system[J].IEEETransonAutomatticControl,1979,24(1):36 -50.
[4]YANG Yuan-xi,GAO Wei-guang.A new learning statistic for adaptive filter based on predicted residuals [J].Progress in Natural Science, 2006, 16(8):833-837.
[5]孙仲康, 周一宇, 何黎星. 单多基地有源无源定位技术[M]. 北京: 国防工业出版社, 1996: 234-241.
[6]樊羚珂. 卡尔曼滤波在被动测距声纳中的应用[J].哈尔滨船舶工程学院学报, 1986, 59-66.
[7]王燕. 水下目标被动定位仿真研究[D]. 哈尔滨工程大学, 2000, 31-33.
[8]刘同明. 数据融合技术及其应用[M]. 北京: 国防工业出版社, 2000, 168-175.
