无刷双馈电机谐波铜耗与铁耗的分析与计算

韩力， 王华， 马南平， 刘航航

(1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044;2.中国煤炭科工集团重庆研究院，重庆400039)

0 引言

无刷双馈电机(brushless doubly－fed machine，BDFM)变频器容量小、转速和功率因数可调，取消了电刷和滑环，提高了系统的可靠性，并可在单馈异步和双馈同步、超同步和亚同步等多种不同方式下稳定运行，在电动机变频调速运行以及发电机变速恒频运行方面具有良好的应用前景［1－3］。但BDFM定子功率绕组、定子控制绕组与转子绕组的极数不等，通过转子的磁场调制作用实现机电能量转换。BDFM转子磁场转换效率不高，气隙中存在很多有害的谐波磁场，从而产生大量的谐波铜耗和铁耗，降低了电机的效率，影响了电机的性能。准确分析和计算BDFM的谐波损耗具有重要意义。

BDFM的结构比常规的异步电机和同步电机复杂，笼型转子采用多回路结构，其端部连接不规则，导致转子回路的电阻、电流计算难度增大;BDFM的转子频率变化范围大，转子的集肤效应和铁耗不能忽略。因此，BDFM损耗的计算方法不同于常规的交流电机，其计算难度要大得多。然而，目前尚未见到对BDFM谐波铜耗和铁耗进行全面分析的报道。文献［2］通过多回路模型计算发现，在亚同步运行状态下，当控制绕组电压增加时，转子电流增加很快，转子铜耗大幅增加，但没有给出转子铜耗的具体计算方法。文献［3］通过时步有限元分析，发现BDFM的磁场分布不规则，认为把传统异步电机中的铁耗计算方法移植BDFM上使用是牵强的。文献［4］采用有限元方法对轴向迭片磁阻转子BDFM不同转速下的损耗进行了分析和计算，结果表明该电机的转子涡流损耗比普通感应电机大很多，但也没有给出铜耗和铁耗的具体计算模型。文献［5－6］采用Bertotti分立铁耗模型计算了BDFM的铁耗，但该模型是基于铁心交变磁化得到的［7－9］，而没有考虑旋转磁化的影响。实际上铁心中存在交变磁化和旋转磁化两种方式，且旋转磁化产生的铁耗占总铁耗的比重较大，不可忽略［10－13］。

针对以上问题，本文提出了适用于BDFM定转子谐波铜耗和铁耗的数学模型，并针对一台带公共笼条的笼型转子BDFM进行了二维场路耦合时步有限元计算和和谐波分析，得到了不同控制绕组电压和负载转矩情况下BDFM电流和铁心磁密的变化规律，然后计算了该电机的定转子铜耗和铁耗，探讨了不同损耗计算模型和运行方式对BDFM铜耗和铁耗的影响。

1 样机结构及基本参数

笼型转子BDFM样机的结构图和转子绕组展开图分别如图1、图2所示。在同一转子巢(nest)中，设6个转子回路从内到外依次编号。样机的基本参数如表1所示。

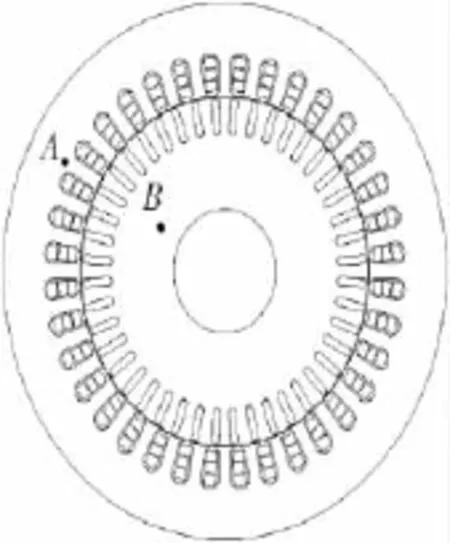
图1 笼型转子BDFM结构Fig.1 Structure of BDFM with cage rotor

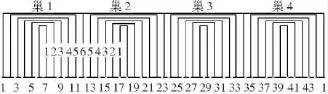
图2 笼型转子展开图Fig.2 Unfolded diagram of the cage rotor

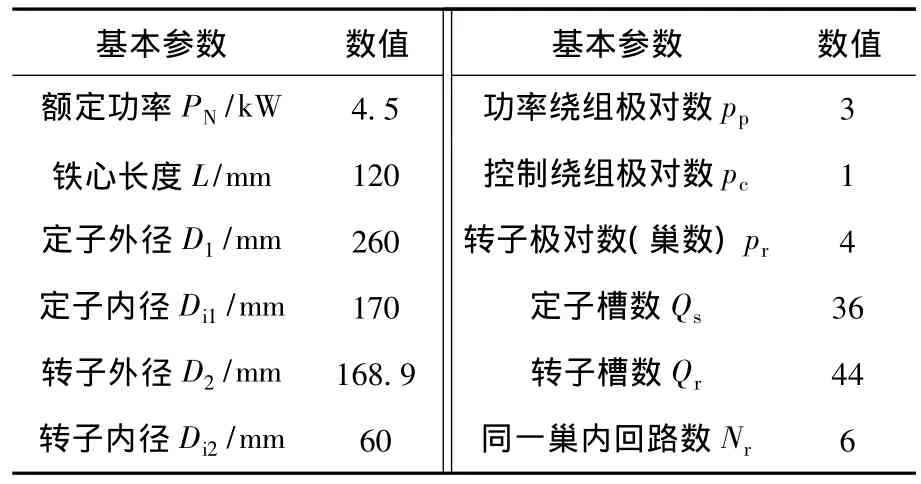
表1 BDFM样机基本参数Table 1 The basic parameters of BDFM prototype

根据文献［14］，定子功率绕组相电阻 Rp=2.032 Ω;定子控制绕组相电阻Rc=2.662 Ω;转子电阻为:每根导条直线部分电阻近似取Rb=0.204 mΩ，各回路端部电阻 Re1=1.63 μΩ、Re2=4.91 μΩ、Re3=8.17 μΩ、Re4=11.4 μΩ、Re5=14.7 μΩ、Re6=17.9 μΩ。

2 损耗计算模型

2.1 场路耦合时步有限元模型

考虑到铁磁材料的饱和问题，描述非线性时变运动电磁场的偏微分方程为［15］

式中:A为矢量磁位;J为电流密度;V为媒质的运动速度;v为媒质的磁阻率;σ为媒质的电导率。

由于BDFM磁场分布的不对称性，选取整个电机作为求解区域，如图1所示。假设电流密度和矢量磁位只有z轴分量，速度只有x轴分量，引入库仑规范。A=0，并加入边界条件，则BDFM二维非线性时变运动电磁场的边值问题为

式中:Az为矢量磁位的z轴分量;Jz为定子绕组电流密度的z轴分量;Vx为速度的x轴分量;Ω为求解区域;Γ为定子外表面和转子内表面，其上Az满足第一类齐次边界条件。

定子功率绕组和控制绕组的耦合电路如图3所示，其电压平衡方程为

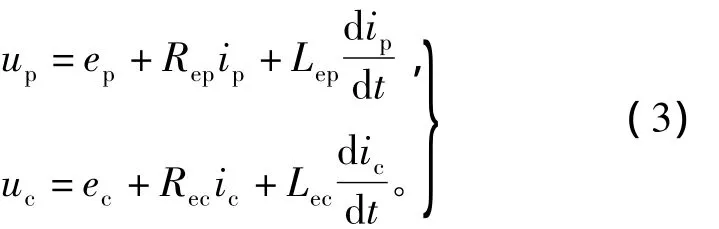
式中:ep、up、ip和 ec、uc、ic分别为功率绕组和控制绕组的感应电动势、电压、电流;Rep、Lep和 Rec、Lec分别为功率绕组和控制绕组的端部电阻和漏感。

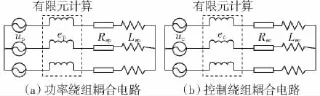
图3 定子绕组耦合电路Fig.3 Coupling circuits of stator windings

功率绕组和控制绕组的感应电动势是连接定子绕组区域和外电路的关键参数，可由定子绕组区域内各单元的平均矢量磁位求出［16］:

式中:Np、Nc分别为功率绕组和控制绕组每相串联导体数;L为铁心长度;Sp、Sc分别为功率绕组和控制绕组一相电流分布区域;Ep、Ec分别为功率绕组和控制绕组区域剖分单元总数;S+e和S－e分别为该相绕组电流流入和流出1个单元的区域;Ae为该单元矢量磁位的平均值。

在二维场中，转子导条中电流只有z轴分量，导条径向截面是一个等势面［3］。根据图4，除公共笼条外，转子内层各回路的电路方程为

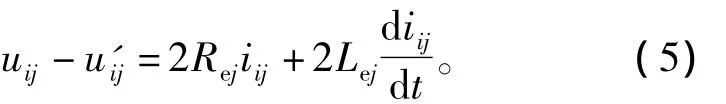
式中:i为转子巢编号，i=1，2，3，4;j为同一转子巢内的回路编号，j=1，2，3，4，5;uij和 u′ij分别为转子第i号巢内第j个回路左边和右边导条的电压降;Rej和Lej分别为第j个回路的端部电阻和漏感。

由于回路编号为6的公共笼条属于两个相邻的转子巢，因此其电路方程不同于内层回路。转子最外层回路的电路方程为

式中:ui6和u′i6分别为第i号巢内左侧和右侧公共笼条的电压降;iei、ie，i+1分别为相邻的第 i号和 i+1号巢的端部电流(当 i为4 时，i+1 轮回到 1)，ii+1，6为第i+1号巢左侧公共笼条的电流;Re6和Le6分别为最外层回路的端部电阻和漏感。

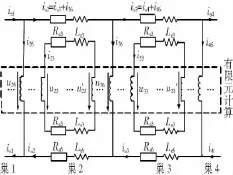
图4 转子绕组耦合电路Fig.4 Coupling circuit of rotor winding

转子导条的电流可通过矢量磁位求出

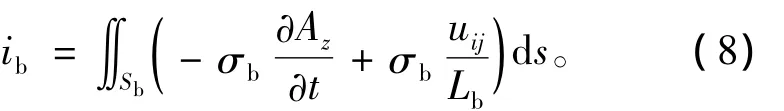
式中:σb为转子导条电阻率;Lb为转子导条直线部分长度;Sb为转子导条横截面积。

上述模型考虑了定转子绕组端部的影响，把二维非线性时变运动电磁场方程和外电路方程结合起来进行求解。采用时步有限元模型式(2)可求出矢量磁位，进而求出磁密，利用式(4)可求出定子功率绕组和控制绕组的感应电动势，利用式(8)可求出转子导条电流。设定子功率绕组和控制绕组分别施加三相对称正弦交流电压，利用式(3)可求出定子绕组的电流。

2.2 定子铜耗计算模型

由于BDFM定子功率绕组和控制绕组均为散嵌导线，线径小，可以忽略集肤效应，因此定子铜耗主要由绕组电流的大小决定。通过对定子绕组电流波形进行傅里叶分解，可得到各次谐波电流的有效值，从而计算出BDFM的谐波铜耗。由于功率绕组和控制绕组均采用三相对称绕组，因此功率绕组铜耗、控制绕组铜耗以及定子绕组的总铜耗可分别表示为

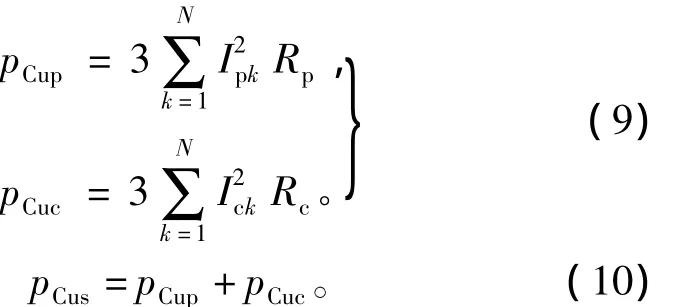
式中:Ipk、Ick分别为功率绕组和控制绕组第k次谐波相电流的有效值;N为谐波次数。

2.3 转子铜耗计算模型

为了便于对比，本文分别采用d－q轴坐标模型和多回路模型计算转子绕组的铜耗。

2.3.1 铜耗模型1

d－q轴坐标模型由精确数学模型变化推出，适用于BDFM转子铜耗的计算。这时，需要首先将三相坐标系模型下转子各回路的电阻变换到d－q轴坐标模型下。转子电阻变换后的参数为

式中:Rrj为同一个巢内第j个回路的转子电阻，Rrj=2(Rb+Rej)。

求出转子等效电阻后，可求出转子铜耗［14］，即

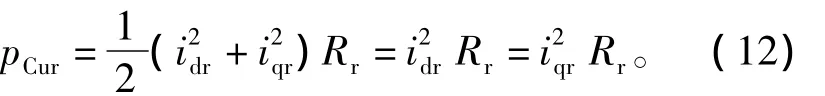
式中:idr、iqr分别为转子电流的d轴和q轴分量。

2.3.2 铜耗模型2

BDFM在正常运行范围内，由于转子频率可能较高，且转子绕组采用单匝导条，因此必须考虑集肤效应对转子电阻与铜耗的影响。

在考虑谐波作用的情况下，集肤效应导致转子导条交流电阻的增加系数为［17］

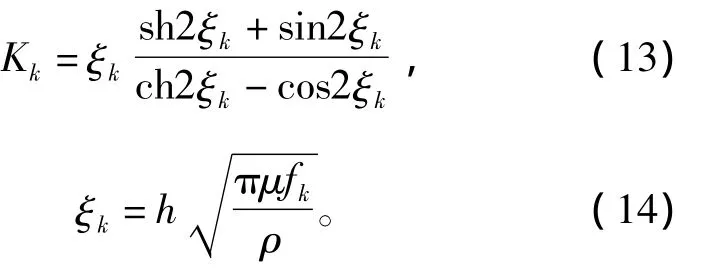
式中:fk为第k次谐波的频率;h为转子导条高度，取值13.2 mm;ρ为转子导条的电阻率，取值4.34×10－8Ω·m;μ为转子导条的磁导率，取值4π×10－7H/m。

下面将采用多回路模型来分析转子铜耗的计算方法。对于本样机，笼型转子总回路数为24，其中4个巢内除公共笼条外，内层共有4×5个独立回路，最外层带公共笼条的回路数为4。由于最外层的公共笼条分属两个相邻转子巢共用，因此其铜耗的计算不同于内层转子回路。在已知集肤效应电阻增加系数的情况下，转子总铜耗pCur可表示为

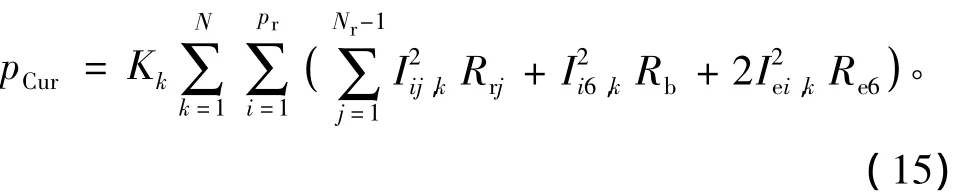
式中:pr为转子巢数;Nr为同一巢内的转子回路数;Iij，k和 Ii6，k分别为转子第 i个巢内第 j个回路和第 6个回路的第k次谐波电流有效值;Iei，k为第i个巢内最外层端环的第k次谐波电流有效值。

2.4 铁耗计算模型

为了准确计算BDFM的铁耗，需要掌握定转子铁心内各部分的磁场分布和变化规律。为了进一步分析谐波磁场对BDFM铁耗的影响，采用如下3种铁耗模型进行计算和对比分析。

表2 三种铁耗模型Table 2 Three models of iron losses

2.4.1 铁耗模型1

Bertotti分立铁耗计算模型仅考虑交变磁化影响，将铁心损耗分为涡流损耗pe、磁滞损耗ph和附加损耗 pa三部分［10－13］，即

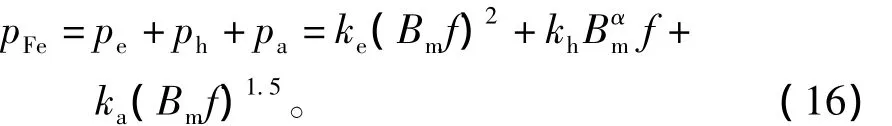
式中:f为基波频率;Bm为基波磁密的幅值;ke为涡流损耗系数;kh、α为磁滞损耗系数;ka附加损耗系数。

本样机定转子铁心采用厚度为0.5 mm的DW 465－50冷轧无取向硅钢片，各系数的取值为［10］:ke=5.6 × 10－5，kh=0.032 584，α =1.778 5，ka=1.191 9 ×10－7。

2.4.2 铁耗模型2

考虑到谐波磁密的影响，铁耗的计算式变为［8］

式中:fk为第k次谐波的频率;Bkm为第k次谐波磁密的幅值。

2.4.3 铁耗模型3

对于交流旋转电机，通常情况下旋转磁化产生的铁耗要比交变磁化产生的铁耗大很多［12－13］。为了进一步考虑旋转磁化的影响，将磁密分解为相互正交的径向分量Br和切向分量Bθ。对图1中定子轭部A点和转子轭部B点，其磁密波形及其频谱分析如图5所示。图6给出了1～5次谐波磁密形成的椭圆型磁场，其长轴磁密为Bkmax，短轴磁密为Bkmin。

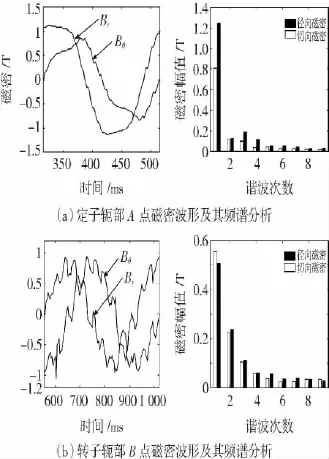
图5 定转子铁心中的磁密Fig.5 The flux densities of stator and rotor cores

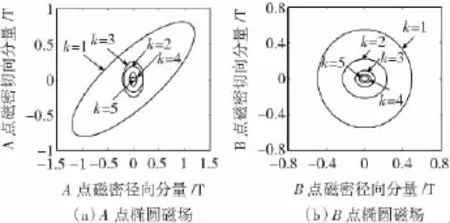
图6 定转子铁心中的椭圆形磁场Fig.6 The elliptical fields of stator and rotor cores

考虑旋转磁化影响时，铁心的涡流损耗、磁滞损耗和附加损耗计算式分别为［10－13］

通过时步有限元分析得到一个周期内每个单元的磁密波形，分别采用式(16)、式(17)或式(18)，可得到3种铁耗模型下该单元单位质量的铁耗。因此，定子铁耗pFes和转子铁耗pFer可分别表示为

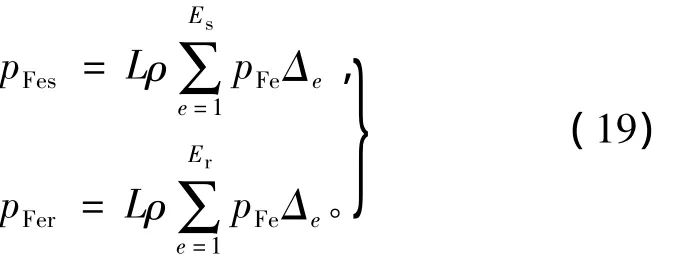
式中:ρ为铁心质量密度;Es、Er分别为定子和转子铁心剖分单元总数;Δe为第e个单元的面积。

最后，可得到定转子铁心的总损耗为

3 计算结果及分析

利用Ansoft/Maxwell软件，采用二维场路耦合时步有限元法，对图1所示的笼型转子BDFM样机进行分析。根据上述定转子铜耗和铁耗计算模型，对BDFM不同运行状态下的损耗进行计算。运行条件为:功率绕组相电压220 V，频率50 Hz，控制绕组和功率绕组相序相同，控制绕组频率13 Hz，BDFM处于超同步恒速运行状态。电机的稳定运行范围为:控制绕组相电压Uc=100～160 V，负载转矩TL=0～30 N·m。研究前提为:在BDFM稳定运行范围内，当TL=0时研究控制绕组电压Uc对损耗的影响，当Uc=130 V时研究负载转矩TL对损耗的影响。为了考虑谐波的影响，以下所有计算谐波次数统一取N=100。

3.1 定子铜耗变化规律

采用二维场路耦合时步有限元模型和谐波分析方法，可得到定子功率绕组和控制绕组的电流波形。在Uc=110 V、TL=0时，定子两套绕组的电流波形及其频谱分析如图7所示。可见，定子功率绕组和控制绕组电流中都存在很多高次谐波，其中控制电流波形畸变更为严重，这势必会增加谐波铜耗。

图8给出了定子绕组铜耗随控制绕组电压和负载转矩的变化曲线。可见，改变控制绕组电压或负载转矩的大小，对定子功率绕组和控制绕组的铜耗都有明显的影响。保持负载转矩TL=0不变，当控制绕组电压Uc升高时，计算表明功率绕组电流先减小后增加(呈V型曲线)、而控制绕组电流逐渐增加，因此功率绕组的铜耗也是先减小后增大，而控制绕组的铜耗逐渐增大。保持控制绕组电压Uc=130 V不变，随着负载转矩TL的增加，功率绕组和控制绕组的输入功率和电流逐渐增加，两套绕组的铜耗也随之增加。相比空载情况，TL=30 N·m时功率绕组的铜耗增加了107.5%，控制绕组的铜耗增加了92.6%，定子总铜耗增加了98.4%。本文所得定子铜耗的变化规律与文献［5］、［18］电流变化规律相同，从而间接验证了本文模型和计算方法的正确性。

图7 定子绕组电流Fig.7 The currents of stator windings

图8 定子铜耗曲线Fig.8 Curves of stator copper losses

3.2 转子铜耗变化规律

图9给出了一个巢内各转子回路电流有效值随控制绕组电压和负载转矩变化的曲线。可见，随着控制绕组电压的增加，各回路电流先减小后增加，其变化规律与文献［19］的实测结果一致;随着负载转矩的增加，各回路电流均随之增大。其中，最外层6号回路电流受控制绕组电压和负载转矩影响最显著，电流上升最快。

图10给出了转子铜耗随控制绕组电压和负载转矩的变化曲线。可见，当TL=0时，随着控制绕组电压的增加，转子铜耗先减小后增大;当Uc=130 V时，随着负载转矩的增加，转子铜耗也逐渐增加。另一方面，转子铜耗模型2的计算结果大于铜耗模型1的计算结果。与铜耗模型2相比，铜耗模型1平均偏差为33%。

图9 转子回路电流曲线Fig.9 Curves of rotor loop currents

图10 转子铜耗曲线Fig.10 Curves of rotor copper losses

3.3 定转子铁耗变化规律

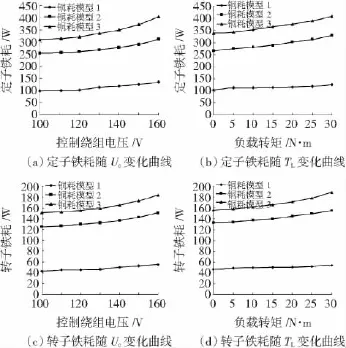
图11 定转子铁耗曲线Fig.11 Curves of stator and rotor iron losses

采用铁耗模型1、铁耗模型2和铁耗模型3，分别计算BDFM定转子铁耗，其变化规律如图11所示。从此可见，随着控制绕组电压和负载转矩的增加，定转子铁耗逐渐增加。对于普通异步电机，由于转差频率很小，因此常常忽略转子铁耗或把转子铁耗归于杂散损耗，然而由于BDFM中存在很多高次谐波磁场，且各次谐波磁场转差频率不同，因此BDFM的转子铁耗不可忽略。另一方面，铁耗模型1的计算结果明显小于铁耗模型2和铁耗模型3的计算结果，由此说明，计算BDFM铁耗时必须考虑谐波磁密和旋转磁化的影响。

3.4 损耗分布规律

表3给出了不同负载转矩下样机的铜耗、铁耗以及总损耗∑p。以Uc=130 V、TL=30 N·m时的运行状态为例进行分析，定转子铜耗占总损耗的76.3%，定转子铁耗占总损耗的23.7%，其中定子控制绕组铜耗占33.3%为最大，定子功率绕组铜耗占22.9%，转子绕组铜耗占20.1%，定子铁耗占16.1%，转子铁耗占7.5%为最小。此时BDFM铜耗与铁耗之和达到2 512.2W，即使忽略机械损耗和杂散损耗，电机的效率还不到56%。

表3 负载转矩对损耗的影响Table 3 The influence of control winding voltage on losses

3.5 实验验证

由于缺乏BDFM样机的实验数据，为了验证上述损耗模型与计算结果的正确性，本文选定一台与BDFM样机的额定容量、额定转速、结构尺寸、有效材料体积以及定转子槽数均接近的Y2－160M2－8异步电机进行对比，该电机的基本参数如表4所示，其铁心采用DR510－50热轧硅钢片，损耗系数ke=1.04 ×10－4，kh=0.041，α =1.892，ka=1.265 ×10－5。

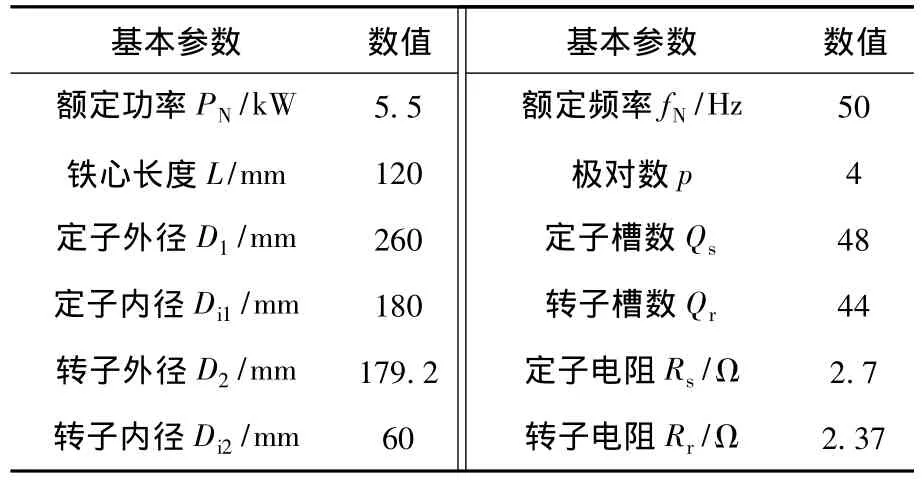
表4 Y2－160M2－8基本参数Table 4 Basic parameters of Y2－160M2－8

采用二维场路耦合时步有限元模型，对Y2－160 M2－8异步电机的转子铜耗和定子铁耗进行计算。表5给出了满载工况下上述模型与试验数据的对比结果，其中试验按照《GB/T1032－2005三相异步电动机试验方法》进行。由此可见，铜耗模型2和铁耗模型3的计算结果更接近实验数据，说明其考虑因素更全面、计算精确度更高。

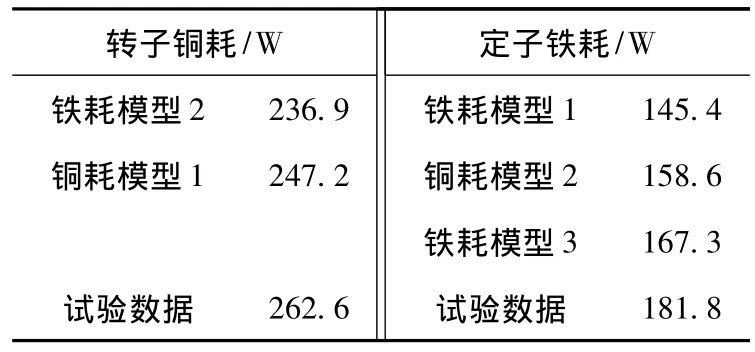
表5 损耗模型计算结果与实验数据对比Table 5 Comparison of the loss models with the experiment

应用转子铜耗模型2以及铁耗模型3对Y2－160M2－8异步电机满载工况进行计算，表6给出了本文模型计算结果与电磁设计数据以及试验数据的对比，其中偏差1、偏差2分别为电磁设计数据、本文模型计算结果与实验数据的比较。

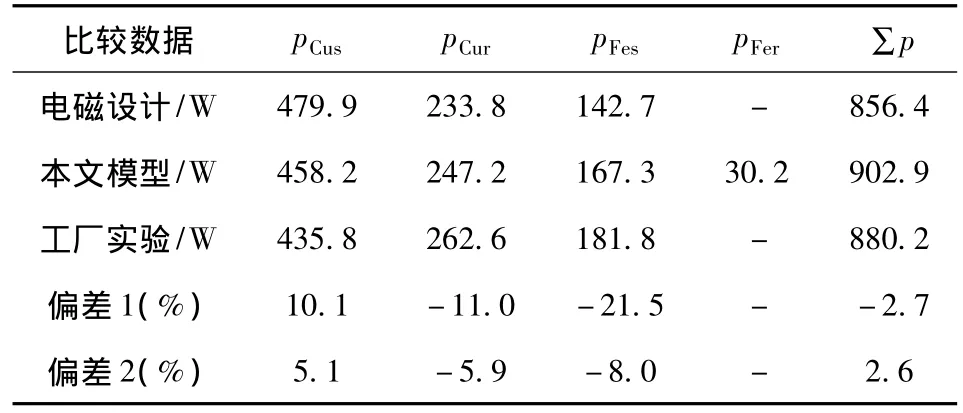
表6 Y2－160M2－8损耗数据对比Table 6 Comparison of Y2－160M2－8 losses data

由表6可见，与电磁设计数据相比，由本文模型计算得到的损耗数据更接近实验数据，从而进一步了验证了本文模型与计算结果的正确性。

4 结论

BDFM定子功率绕组、定子控制绕组与转子绕组的极数不等，通过转子的磁场调制作用实现机电能量转换。笼型转子BDFM结构复杂，谐波含量高，磁场分布不规则，转子集肤效应明显。以上因素均导致了准确计算笼型转子BDFM铜耗与铁耗的难度增大。

针对笼型转子BDFM谐波铜耗与铁耗计算的复杂性，建立了两种转子铜耗计算模型和3种铁耗计算模型，其中转子铜耗模型2同时考虑了谐波电流、集肤效应和转子端环的影响，铁耗模型3同时考虑了谐波磁密以及交变磁化和旋转磁化的影响。通过与相似的Y2系列异步电机损耗试验数据比较，验证了转子铜耗模型2和铁耗模型3具有更高的计算精确度。以上结果为笼型转子BDFM的谐波损耗计算以及下一步的发热分析奠定了理论基础。

在控制绕组频率不变、保持BDFM超同步恒速运行的情况下，随着控制绕组电压的增加，定转子铜耗先减小后增加，定转子铁耗持续增加;随着负载转矩的增加，定转子铜耗和铁耗均随之增加。

［1］ S Williamson，A C Ferreira，A K Wallace.Generalised theory of the brushless doubly-fed machine.Part1:Analysis［J］.IEE Proceedings Electric Power Applications，1997，144(2):111 －122.

［2］ 张爱玲，熊光煜，刘振富，等.无刷双馈电机能量传递关系和功率因数特性的实验研究［J］.中国电机工程学报，2011，31(6):92－97.

ZHANG Ailing，XIONG Guangyu，LIU Zhenfu，et al.Experimental study on energy transmission and power factor characteristics of brushless doubly-fed Machines［J］.Proceedings of the CSEE，2011，31(6):92－97.

［3］ 王爱龙，熊光煜.无刷双馈电机时步有限元分析［J］.中国电机工程学报，2008，28(21):123－127.

WANG Ailong，XIONG Guangyu.Analysis of brushless doublyfed machine by time stepping finite element method［J］.Proceedings of the CSEE，2008，28(21):123－127.

［4］ I Scian，D G Dorrell，Piotr J Holik.Assessment of losses in a brushless doubly-fed reluctance machine［J］.IEEE Transaction on Magnetics，2006，42(10):3425－3427.

［5］ A C Ferreira，S Williamson.Time-stepping finite-element analysis of brushless doubly fed machine taking iron loss and saturation into account［J］.IEEE Transaction on Magnetics，1999，35(3):583－588.

［6］ 杨向宇，励庆孚，郭灯塔.无刷双馈电机铁心损耗计算与饱和效应的分析研究［J］.电工电能新技术，2002，21(1):54－57，72.

YANG Xiangyu，LI Qingfu，GUO Dengta.Study on iron loss and saturation in brushless doubly-fed machines for adjustable speed drive［J］.Advanced Technology of Electrical Engineering and Energy，2002，21(1):54 －57，72.

［7］ 胡笳，罗应立，李志强，等.永磁电动机不同运行条件下的损耗研究［J］.电机与控制学报，2009，13(1):11－16.

HU Jia，LUO Yingli，LI Zhiqiang，et al.Investigation of losses in permanent magnet synchronous motor under different operation conditions［J］.Electric Machines and Control，2009，13(1):11－16.

［8］ 韩力，谢李丹，张桂娟.变频器参数对永磁同步发电机定子损耗的影响［J］.电机与控制学报，2010，14(12):75－81.

HAN Li，XIE Lidan，ZHANG Guijuan.Influence of converter parameters on stator losses of permanent magnet synchronous generator［J］.Electric Machines and Control，2010，14(12):75 －81.

［9］ LEE Jeong-Jong，KIM Young-Kyoun，NAM Hyuk.Loss distribution of three－phase induction motor fed by pulsewidth－modulated inverter［J］.IEEE Transactions on Magnetics，2004，40(2):762－765.

［10］ 余莉，胡虔生，易龙芳.高速永磁无刷直流电机铁耗的分析与计算［J］.电机控制与应用，2007，34(4):10－14，32.

YU Li，HU Qiansheng，YI Longfang，et al.Analysis and calculation of the iron losses of high speed permanent motors［J］，E-lectric Machine＆ Control Application 2007，34(4):10－14，32.

［11］ Zhu J G，Ramsden V S.Improved formulation for rotational core losses in rotating electrical machine［J］.IEEE Transactions on Magnetics，1998，34(4):2234－2242.

［12］ 张洪亮，邹继斌.考虑旋转磁通的PMSM铁心损耗数值计算［J］.电机与控制学报，2007，11(4):340－344，348.

ZHANG Hongliang，ZOU Jibin.Numerical calculation and analysis of stator iron losses due to rotational flux and magnet pole eddy-current loss in PMSM［J］.Electric Machines and Control，2007，11(4):340－344，348.

［13］ 孔晓光，王凤翔，徐云龙，等.高速永磁电机铁耗的分析和计算［J］.电机与控制学报，2010，14(9):26－30.

KONG Xiaoguang，WANG Fengxiang，XU Yunlong，et al.Analysis and calculation of iron losses of high-speed permanent magnet machines［J］.Electric Machines and Control，2010，14(9):26－30.

［14］ 刘航航.无刷双馈电机磁场调制机理与电磁设计研究［D］.重庆:重庆大学电气工程学院，2011:29－30，62.

［15］ 严登俊，刘瑞芳，胡敏强，等.处理电磁场有限元问题的新方法［J］.中国电机工程学报，2003，23(8):163－167.

YAN Denjun，LIU Ruifang，HU Minqiang，et al.A new method to deal with the motion problem in electromagnetic field finite element analysis［J］.Proceedings of the CSEE，2003，23(8):163－167.

［16］ 胡敏强，黄学良.电机运行性能数值计算方法及其应用［M］.南京:东南大学出版社，2003:173－175.

［17］ 陈世坤.电机设计.2版［M］.北京:机械工业出版社，1990:64－72.

［18］ 邓先明.无刷双馈电机的电磁分析与设计应用［M］.北京:机械工业出版社，2008:153－157.

［19］ Abdi-Jalebi E，McMahon R.Application of real-time rotor current measurements using bluetooth wireless technology in study of the brushless doubly-fed(induction)machine(BDFM)［C］//Industry Applications Conference，October 8 －12，2006，Tampa，FL，USA.2010，1557－1561.