全圆齿根设计及其应力特性研究
2012-07-03马贵叶张祖智杜万里
马贵叶,张祖智,杜万里,刘 越
(中国北方车辆研究所车辆传动重点实验室,北京 100072)
齿轮是车辆传动系统动力传递的关键基础件,车辆的直驶、转向和制动等功能均通过齿轮传递来实现.断齿、偏载点蚀等是传动系统中齿轮疲劳损坏的主要形式,是导致车辆动力传递中断,车辆丧失战斗力的典型故障.轮齿根部是抗弯强度的危险部位[1],如果齿轮根部圆角小,就容易产生应力集中,承载能力就降低.因此,为了提高齿轮的抗疲劳损坏,减轻硬齿面齿轮根部应力集中,有必要讨论轮齿根部采用全圆弧槽形对轮齿弯曲强度的影响,并给出合理的齿根全圆弧半径等参数,以便该技术在工程中推广应用.
1 全圆齿根参数确立
1.1 齿根过渡曲线介绍
如图1和图2所示,由齿轮啮合原理和展成运动可知[2-3],齿轮的渐开线齿面CD,是由刀具腰线部分EF在切齿中包络形成的,而齿轮齿根过渡曲线BC,则是由齿条刀具齿顶的圆弧部分FG在切齿中包络形成的,这一部分刀刃加工出来的齿廓不是渐开线,不能参与啮合.但是齿根过渡曲线的曲率半径大小与齿轮弯曲强度关系非常密切.齿根过渡曲线曲率半径越大,越有利于提高齿轮弯曲强度.
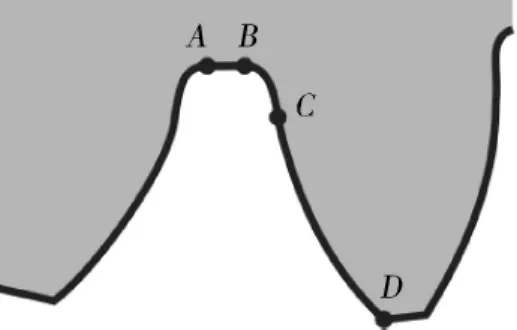
图1 渐开线齿形

图2 齿条刀具
对于模数m≥1 mm的渐开线圆柱齿轮,其基本齿廓一般采用现行的GB1356—87《渐开线圆柱齿轮基本齿廓》,其中齿根圆角半径为0.38m.在这种情况下,齿根过渡曲线曲率半径较小.通过增加刀具圆角半径,可增大齿根过渡曲线曲率半径.全圆滚刀的顶部为全圆弧,加工得到的全圆弧槽形齿根齿轮,其齿根过渡曲线曲率半径大、强度高.因此,在考虑全圆滚刀刀具加工的基础上,通过求解渐开线起始圆半径,反推出加工全圆弧槽形齿根齿轮的合理的全圆滚刀刀具参数.
1.2 渐开线起始圆半径求解
渐开线起始圆半径就是相啮合的渐开线的终止点 (齿顶圆与渐开线的交点,如图3所示的点K)与本齿轮渐开线的根部啮合点的位置半径.
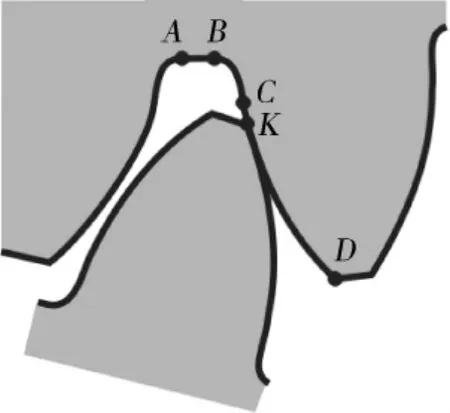
图3 齿根过渡曲线较小
如图4所示,O1、O2是两个相啮合的渐开线齿轮的中心.M1M2是啮合线.A、B分别是小轮、大轮齿顶圆与啮合线M1M2的交点.则由啮合原理可知,O1A、O2B分别为小轮、大轮的渐开线起始圆半径.如图4所示,啮合线M1M2的长度为:

图4 渐开线起始圆最大半径
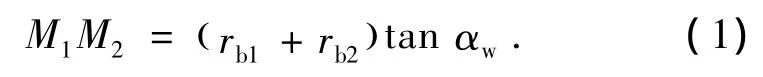
式中:rb1为小轮基圆半径;rb2为大轮基圆半径;αw为啮合角.
在直角三角形O2AM2中,有:
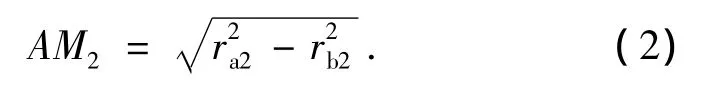
式中:ra2为大轮齿顶圆半径.
因此,有:
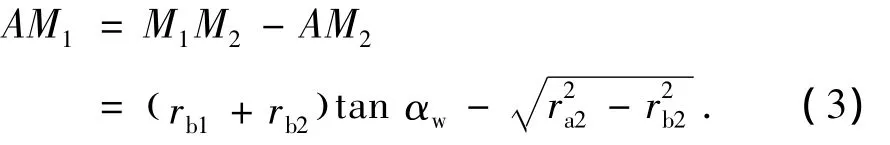
在直角三角形O1AM1中,有:
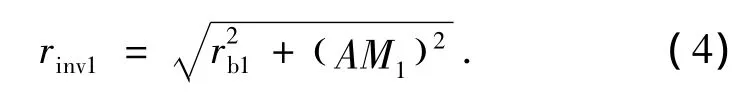
式中:rinv1为小轮的渐开线起始圆半径.
体育彩票自1994年发行以来,在推进全民健身活动、奥运战略及社会公益事业等方面发挥着重要作用,同时为促进我国体育事业发展产生着积极影响。通过文献梳理可知,对于体育彩票领域的研究较多是体育彩票产业现状、社会效应、政策解读等方面的质性研究。量化研究更多的是从彩票购买者角度为出发点的实证研究。李凌(2015)等初步探讨了消费者购买竞猜型体育彩票的影响因素[1],通过结构方程模型验证了消费者购买竞猜型体育彩票的偏好路径[2],最后通过定性与定量结合的方法探讨体育赛事观赏与竞猜型体育彩票的影响效果[3]。
将式(3)代入式(4)中,得到小轮的渐开线起始圆半径求解公式为:

式中:ra2为大轮齿顶圆半径.
同理,大轮的渐开线起始圆半径求解公式为:
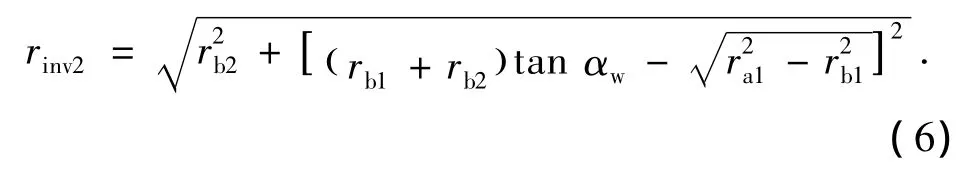
式中:ra1为小轮齿顶圆半径.
1.3 全圆滚刀形状及其参数
求出大轮、小轮的渐开线起始圆半径后,就可以绘制出全圆滚刀形状,如图5所示.为求解其圆角半径及圆心位置,以加工小轮的全圆滚刀为例,有:

式中:rO1为加工小轮的全圆滚刀圆角半径;hO1为小轮全圆滚刀圆角的圆心位置;rp1为小轮节圆半径;rinv1为小轮渐开线起始圆半径;s为节圆弧齿厚;α为齿形角或压力角.
同理,也可得到加工大轮的全圆滚刀圆角半径rO2及其圆心位置hO2,在此不再赘述.
如果考虑齿根挖根量uFP,则全圆滚刀形状如图6所示.
为求解其圆角半径,以加工小轮的全圆滚刀为例.在三角形VC'G中,有:
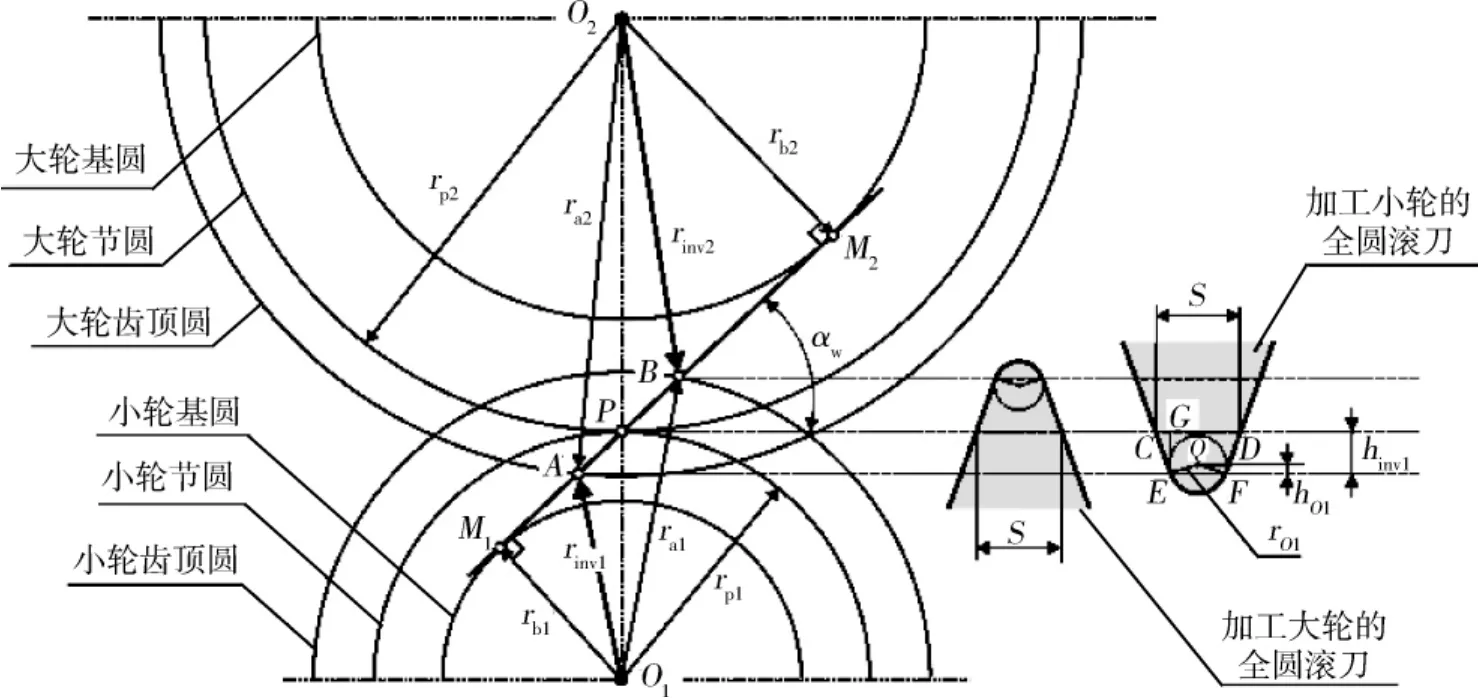
图5 全圆滚刀参数几何图

图6 考虑挖根量的全圆滚刀几何形状

在三角形VEQ中,有:

式中:rFP1为考虑挖根量的小轮全圆滚刀圆角半径;hFP1为小轮全圆滚刀圆角的圆心位置;hinv1求解见式(8).
在三角形JKQ中,有:
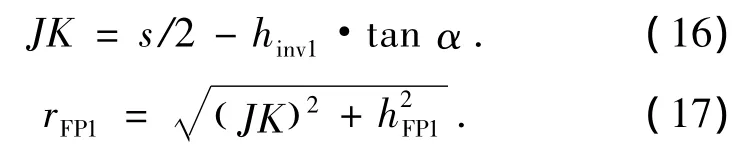
由式(15)、式(17),可得关于hFP1的一元二次方程:

由式(18)可求解出hFP1.根据式(17)求出rFP1.同理,也可得到加工大轮的全圆滚刀圆角半径rFP2及其圆心位置hFP2,在此不再赘述.
在实际的工程应用中,选用的全圆滚刀刀尖圆角半径为:
(1)小轮:rO1~rFP1之间;
(2)大轮:rO2~rFP2之间.
2 齿根应力分析
以表1所示参数的齿轮为例,通过仿真渐开线齿轮的切齿过程,采用0.38m大小圆角的刀具和全圆滚刀,分别建立了不同齿根圆角过渡曲线的齿轮三维仿真模型.

表1 齿轮参数

图7 齿根应力对比分析
在Ansys有限元软件中进行受载仿真,作用同样的载荷,考查齿根应力状况,如图7所示.其中,0.38m圆角小轮受载齿根应力最大值为946.034 MPa,大轮为842.742 MPa;全圆齿根小轮受载齿根应力最大值为629.709 MPa,大轮为809.764 MPa.小轮齿根应力降低33%,大轮齿根应力降低4%.
由疲劳理论可知[4],疲劳失效以前经历的应力循环次数N和应力水平α有如下关系:

式中:m和C为与材料有关的常数.
由式(19)可知,应力水平α越大、应力循环次数N越小.由于小轮转速高,在相同时间内应力循环次数明显多于大轮,因此一般来说小轮是一对啮合齿轮中使用寿命较短的一方.因此,降低小轮的齿根应力,可以提高小轮的应力循环次数,有助于提高啮合副的整体的使用寿命.
从仿真分析结果来看,小轮齿根应力得到大幅削减,大轮齿根应力也得到了削减.因此,全圆滚刀展成的齿轮的齿根过渡曲线可以减小齿根应力,降低齿根峰值应力,从而提高轮齿承载能力和使用寿命.
3 结论
利用齿轮生成范成法,推导出了全圆滚刀参数的求解公式;建立了全圆弧过渡曲线轮齿和通用过渡曲线轮齿 (0.38m齿根过渡曲线)三维仿真模型,并采用有限元方法对其进行应力分析和比较,结果表明:小轮齿根应力降低33%,大轮齿根应力降低4%.因此,采用全圆弧过渡曲线的轮齿齿根可提高轮齿弯曲强度.
[1]郁明山.齿轮手册 (下册)[M].北京:机械工业出版社,2007.
[2]曾 韬.螺旋锥齿轮设计与加工 [M].黑龙江:哈尔滨工业大学出版社,1989.
[3]吴序堂.齿轮啮合原理[M].西安:西安交通大学出版社,2009.
[4]赵少卞.王忠保[M].抗疲劳设计——方法与数据[M].北京:机械工业出版社,1997.
