LTE-A系统中球形译码检测算法研究*

陈发堂，梁涛涛，李小文

（重庆邮电大学 通信与信息工程学院，重庆400065）

LTE-A是一个后向兼容LTE的演进技术。主要的关键技术有多频段协同与载波聚合，并且上行支持多天线技术，下行最高支持8×8多天线配置规格，在100 MHz频谱带宽下能够提供上行500 Mb/s与下行1 Gb/s的峰值速率。上下行峰值频谱利用率分别达到15(b/s)/Hz和30(b/s)/Hz。这些参数则远超越4 G的最小要求[1]。

多输入多输出（MIMO）技术是组成LTE-A的关键技术，目前 LTE的多天线设计支持 4×4配置[2]，而 LTEA增加了天线配置。多天线技术可以带来固有增益达到很高的频谱利用率。接收端的检测算法对于这种优势起着至关重要的作用,常用的有迫零（ZF）[3]、最小均方误差 （MMSE）[4]、最 大 似 然 （ML）译 码[5]。 由 于 ZF 或 者MMSE译码算法的计算复杂度主要与信道传输矩阵求逆矩阵相关，实现相对简单，但是性能不是很好；接收端采用ML译码可以获得最佳性能，但是由于搜索点数与被选集合、天线数目相关，搜索次数过于庞大，工程实现很困难。为了减少ML译码计算复杂度，最根本的就是减少搜索点数。球形译码[6]正是基于这种思想，用较少的计算量获得近似最大似然译码性能。

[7]提出了一种减小球形译码初始化半径方法，主要基于目标误比特率（BER）性能确定仿真比特数，然后根据比特数和调制方式、发射天线数计算出初始半径系数α,最后结合信道噪声方差计算出初始半径。但是这种方法不能保证所选取的球内肯定存在网格点，所以需要重新搜索，增加了球形译码的复杂度。针对上述问题，参考文献[8]提出一种基于接收信号最小均方误差（MMSE）解选取初始半径的方法，解决了因初始半径过小，导致球内没有网格点，另一方面对于低信噪比下，复杂度得到降低。但是该方法在较高信噪比条件下，复杂度并没有降低。针对以上问题，本文提出一种基于阈值的半径选择方法,在准确确定球形译码的初始半径，保证球形译码性能的前提下，降低球形译码算法复杂度。满足LTE-A系统对复杂度和性能的要求,适用于LTE综合测试仪表。

1 系统模型

对于LTE-A系统，采用M根发射天线，N根接收天线，其中M≤4，N≤8。信道为静态平坦衰落情况，信道传输方程为：其中，是接收信号矢量,=[y1,y2,…yN]T是发射信号矢量，=[x1,x2,…xM]T,其中 xi是 M-QAM调制星座图中的复值点；∈CN×M是 N行 M 列的信道传输矩阵；∈CN×1是加性高斯白噪声。在瑞利信道和独立同分布的前提下的每个元素满足复高斯分布，噪声方差为σ2。设发送端总功率为1，则每根接收天线上平均信噪比SNR为1/σ2。

式(1)中每个变量的元素都是复数，因此向量与矩阵维数都扩展 2倍，令m=2M,n=2N,将式(1)中复数形式转化为实数形式[9]，得：

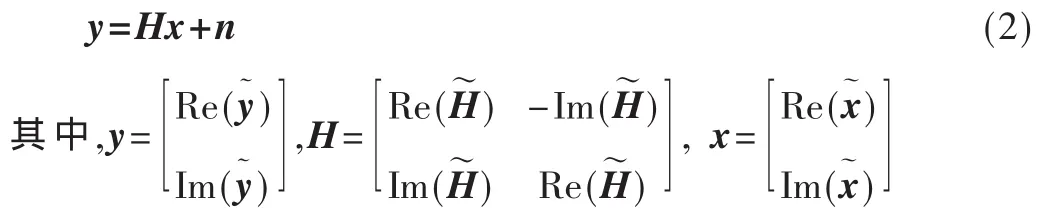
转化后，方程(2)中的元素都是实数值，ML译码过程就是寻找令‖y-Hx‖2最小的向量组合。虽然最大似然译码可以获得最佳的译码性能，但是需要搜索所有点，所以计算量非常大。例如，收发天线M=N=4,LTE-A系统采用64-QAM调制，向量x在接收端有68=1 679 616＞106种可能性。最大似然译码的计算复杂度随着天线数目和调制阶数呈现指数关系增加，工程不可能实现，所以球形译码成为工程实现的优选方案。

2 球形译码算法及半径选择方案

球形译码原理非常简单，算法的基本思想是：搜索位于一个半径为d的超球内的样本点，这样就降低了搜索的计算复杂度，在超球内部的样本点集合中，距离接收信号最近的点就是全局距离最近的点。但是关键问题是如何确定球的半径d，如果d太大，在超球内点太多，搜索量会大大增加，达不到减少复杂度的目的；如果d选的太小，又会导致超球内没有备选点。

2.1 球形译码算法

根据球形译码原理[6]满足式(3)的向量～x为最佳选择。其中d为搜索半径，对信道矩阵H进行QR 分解，矩阵大小为 N×M，其中n≥m，可得下式:

其中R是m×m的上三角矩阵，并且Q=[Q1Q2]是一个n×n的正交矩阵，矩阵Q1和Q2分别代表矩阵 Q的前m列和n-m列，因此式(3)可以变化为：

其中(·)*为厄密矩阵变换。公式(5)可以变化为：

已知式(9)不是充分条件，当选中满足条件的xm时，计算下一个值xm-1，这时需要更新半径=d′2-(ym-rm,mxm)2，并且，ym-1|m=ym-1-rm-1,m,nxm,根据式(8)可确定一个 xm-1，继续计算下一个值 xm-2，直到 x1。

下面给出球形译码算法的具体步骤：

(4)xk=xk+1,如果 xk≤UB(xk)，则跳至步骤(6)，否则跳至(5)。

(5)k=k+1,如果 k=m+1，终止计算，否则，跳至步骤(4)。

(7)找到结果，将数组 x，以及Hx与接收信号y的差距-d1′2+(y1-r1,1y1)2，并且跳至步骤(4)。

2.2 半径选择

在工程应用中，常用的半径选择方法有基于误比特率(BER)的半径系数选择法[7]和基于最小均方差(MMSE)的半径选择法[8]。在此基础上，提出基于阈值的改进型半径选择算法。

2.2.1 基于BER的半径系数选择法

这种半径选择方法是一种根据调制方式和欲达到的目标BER值BERtarget来定义初始半径系数值α的方法。

下面给出算法的具体步骤：

(1)根据定义目标BER性能，则可以获得需要仿真比特数Nsim_bit=100/BERtarget，即至少统计100个错误比特。

(2)根据比特数和调制方式确定符号数,即Nsim_symbol=Nsim_bit/mode_order， 其中 QAM、16 QAM、64 QAM 对应的调制阶数 mode_order为 2、4、6。

(3)根据符号数以及系统的发射天线的数目计算初始化半径系数α，相应地，可以根据下式得到初始化半径系数α：

其中 Γ(·）为gamma函数。 根据条件可以计算出 1-ξ，即可得到对应的α，但是为了降低计算复杂度，在计算之前首先将α与1-ξ的对应关系存表。在工程实现中可以根据1-ξ快速从表 1查得相应的 α。最终半径定义为：r2=αnσ2,其中σ2为噪声方差，n为两倍的发射天线数目。

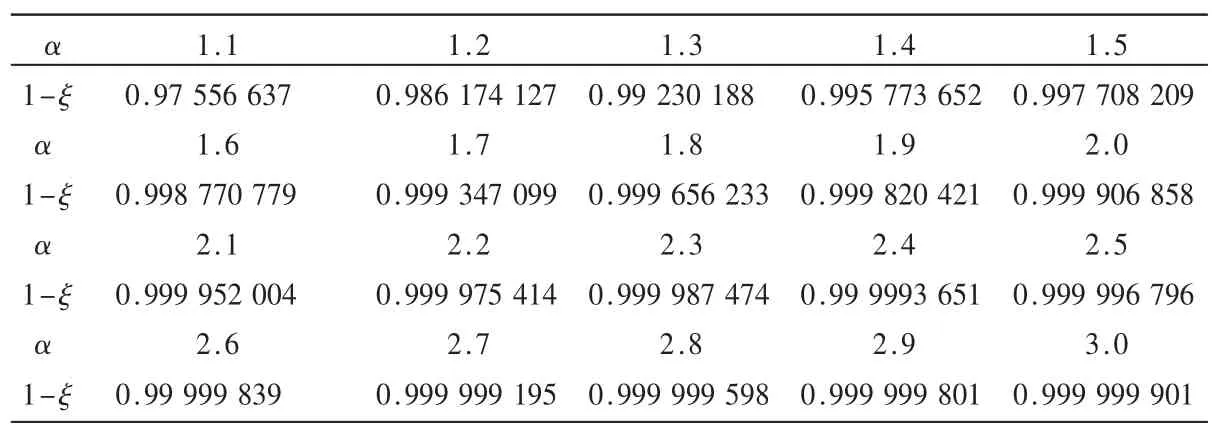
表1 α与1-ξ对应关系表

2.2.2 基于MMSE的半径选择法

基于接收端MMSE算法的信道估计，可以得到最小均方差解：

其中，y为接收信号，I为单位矩阵，σ2为噪声方差；对进行基于硬判决的解调，得到相应的网格点，并且利用信道矩阵H进行重构得到，具体过程参考图1。初始半径 d：d=‖y-‖。

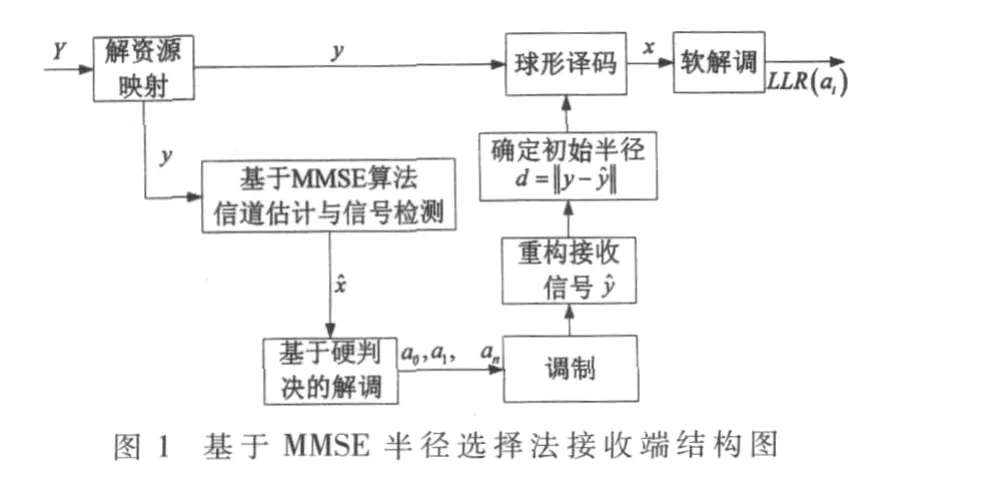
由以上分析可知，如果半径d设置太大，则增加复杂度；如果太小可能又会导致超球内没有备选点。而基于MMSE的半径选择法可以保证至少存在一个网格点，从而避免对初始半径进行重新搜索的问题。

2.2.3 基于阈值的半径选择法

基于BER的半径系数选择法不能保证所选取的球内肯定存在网格点，从而可能需要重新进行搜索；在信噪比相对比较低的情况下，由于噪声方差较大，导致选取初始半径d过大，这样会增加球形译码的复杂度。而基于MMSE的半径选择法不仅避免了因初始半径d过小，导致初始球内没有网格点的情况，而且对于低信噪比条件下，球形译码复杂度得到降低。但是，在相对信噪比比较高的条件下，其球形译码复杂度有时并没有降低，甚至有时还要增加复杂度。针对这种情况，本文提出一种基于阈值的半径选择方法。具体步骤如下：

(1)计算当前信道的条件数和信噪比，球形译码对信道条件敏感，而条件数本身是衡量信道对发射信号星座图扭曲程度的最直接参数,条件数 Ncond=‖H‖*‖H-1‖，条件数越大矩阵越病态；而信噪比可以通过空载波在接收端进行测量。

(3)根据调制方式和目标误比特率确定对应要求的信噪比 SNRtarget，然后根据SNRtarget计算阈值：Threshold=λ1*SNRtarget-λ2,其中 ，1＜λ1＜1.8，3＜λ2＜4。

2.3 改进型球形译码算法流程

图2给出了改进型球形译码算法流程，本文采用基于阈值的半径选择算法。需要注意的初始化参数包括：经过QR分解后的矩阵Q=[Q1Q2]、R以及初始化半径

形译码算法将存储所有满足半径的输入向量集合x以及对应的误差，最后判断误差最小的向量为最佳向量。如果半径设置过大，则输出满足的集合过多，就会额外增加计算的复杂度。

3 仿真验证及性能分析

通过MATLAB7.0对上述三种算法进行仿真。仿真采用如表2所示的统一条件和参数。需要说明，权重系数 β=0.7，目标 SNRtarget=9 dB, λ1=1.5,λ2=3.5，基于 LTEA系统仿真，仿真次数为2 000次，每根发射天线发送的符号数为t=100。其中ML为最大似然检测算法，MMSESD为基于MMSE解的半径选择法，BER-SD为基于误比特率的半径系数选择法，Threshold-SD为改进的基于阈值的半径选择法。

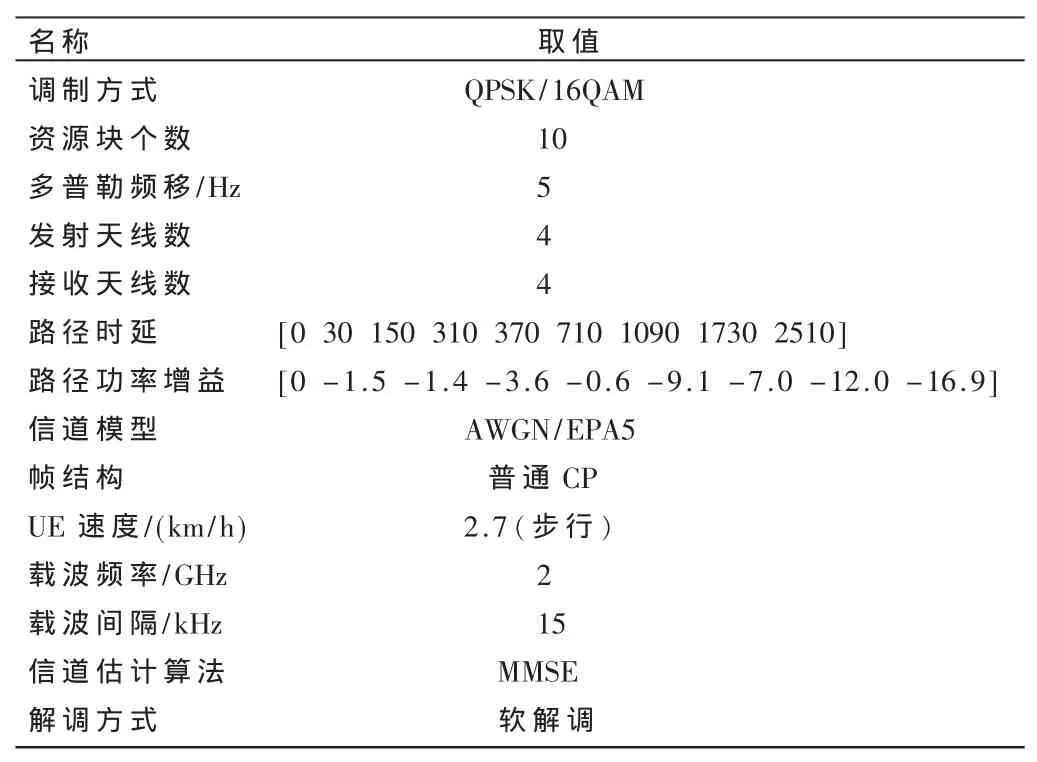
表2 仿真条件和参数

仿真结果分析：当发送端采用QPSK调制方式时，基于BER的球形译码算法更接近ML算法。在信噪比较低时，MMSE算法接近BER算法，但是从图3～图7可知，MMSE算法复杂度要明显低于BER算法；在中高信噪比下，MMSE算法性能明显低于BER算法，并且MMSE算法的复杂度高于BER算法。对比图3与图5可知，随着天线数目增加，这种性能差距越来越大。结合复杂度和性能，本文设定目标SNRtarget=9 dB，当信噪比小于9 dB时，基于阈值算法性能和复杂度趋近于MMSE算法，但较ML算法有不到5%的误码性能损失。随着信噪比增加，基于阈值算法性能和复杂度趋近于并无限接近BER算法。当发送端采用16 QAM时，在相同天线条件下，改进算法性能较MMSE算法提升20%。所以随着天线数目和调制方式增加，改进型算法优势更加明显。

如图7所示给出了四天线采用QPSK的情况下，各种算法的计算复杂度对比，采用搜索星座点数衡量计算复杂度。在信噪比小于9 dB时，改进型基于阈值的算法复杂度偏向于MMSE球形译码检测算法，并且随着信噪比的增加这种趋势越来越明显。当信噪比大于9 dB时，改进型算法开始偏向于BER球形译码的复杂度，因为MMSE算法和BER算法的复杂度在9 dB左右发生变化，所以在改进型算法中，设定的目标信噪比为9 dB。

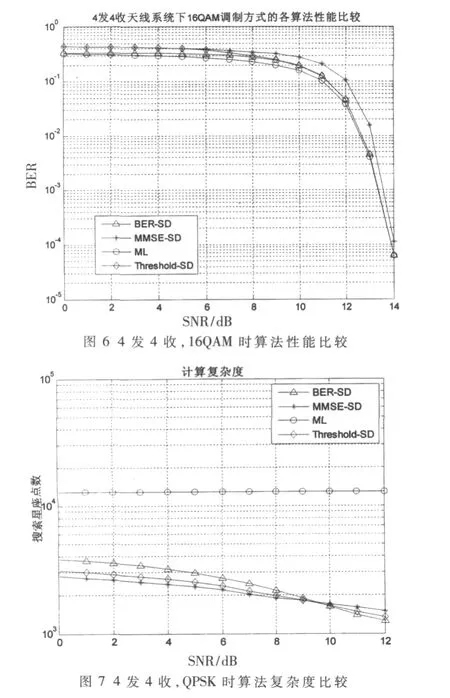
通过上述分析可知，当小于9 dB时，改进型算法偏向于采用复杂度低，但是性能接近BER的MMSE球形译码算法，虽然在小于门限值时，采用MMSE半径，但是复杂度与MMSE算法的复杂度并不相同，这是因为受到信道条件数的影响，信道条件数是根据不同的随机信道矩阵而变化的，所以复杂度只能接近，而不相同。当大于9 dB时，改进型算法偏向于采用复杂度低,但是性能更优的BER球形译码算法。

综上所述,本文提出的基于阈值的球形译码算法，因为考虑到信道条件数和信噪比对译码性能的影响，综合两种算法的性能和复杂度优势，用不到5%的误码性能损失，却获得接近40%的性能提升，保证在每种信噪比下，都能通过低复杂度获得较好性能。在保证球形译码性能前提下，该算法对于低复杂的信号检测工程实现是十分理想选择。

本文针对基于LTE-A系统下传统球形译码检测算法，提出一种基于阈值的改进球形译码检测算法，该算法考虑到信道条件数和信噪比对译码性能的影响，不仅保证了低、中信噪比下的性能，还降低了复杂度；而且，在高信噪比时，采用复杂度低，性能更优越的译码方案。总之，在保证球形译码性能的同时，大大降低了球形译码的计算复杂度。该算法已应用于LTE无线综合测试仪中。

参考文献

[1]3GPP TR 36.913.Requirements for further advancement for Evolved Universal Terrestrial Radio Access(E-UTRA)[EB/OL].(2007-07-15).[2009-06-12].http://www.3gpp.org/ftp/specs/html-info/36913.htm.

[2]3GPP.TS 36.211 v9.0.0 evolved universal terrestrial radio access(E-UTRA)LTE Physical Layer-General Descripti on(Release 9)[EB/OL].(2009-12-31).[2011-03-15].http://www.3gpp.org.

[3]Zheng Shanshan,Chen Xia,Tan Zhenhu.Detection algorithms for V-BLAST systems[J].Wireless communication technology,2006,4:23-27.

[4]WUBBEN D， BOHNKE R，RINAS J，et al.Efficient algorithm for decoding Layered Space-Time Codes[J].IEEE Electronic Letters，2001,37(22):1348-1350.

[5]NEE R Va,ZELST A V,AWATER G.Maximum likelihood decoding in a space division multiplexing system[C].Proc.Of IEEE Vehicular Technology Conference.2000,Tokyo,2000，1(5):6-10.

[6]HASSIBI B,VIKALO H.On the sphere-decoding algorithm I.Expected Complexity[J].IEEE Transactions on Signal Processing,2005,53(8):2806-2817.

[7]夏小梅，胡宏林，赵巍，等.减小球形译码初始化半径方法[P].中国，200610116780.1.2008-04-02.

[8]Liu Qianlei,Yang Luxi.A novel method for initial radius selection of sphere decoding[C].IEEE semiannual Vehicular Technology Conference VTC-Fall,2004.Los Angeles,USA,IEEE,2004:1280-1283.

[9]Chin Yunhung,SANG T H.A sphere decoding algorithm for MIMO channels[J].IEEE International Symposium on Signal Processing and Information Technology,2006,1(3):504-506.