小型连接件尺寸高精度测量研究*
2012-07-03钟绍俊
俞 甫,钟绍俊,谢 敏,孙 坚
(中国计量学院 机电工程学院,浙江 杭州 310018)
小型连接件广泛应用于电子拔插设备中,其尺寸是否合格直接影响电子产品的使用寿命。机器视觉是一种基于图像处理技术的非接触式测量技术,检测结果精确、可靠。在尺寸检测中,一般采用短焦距定焦光学镜头,因此不可避免地将引入非线性畸变。另外,机器视觉图像处理的结果通常为像素个数,实际应用中需要得到像素与实际尺寸之间的关系,才能换算出实际尺寸,所以需要进行摄像机标定得到畸变参数和像素当量[1-2]。
亚像素检测方法目前已被广泛应用于高精度测量中,亚像素表示图像中每个像素将会被分为更小单元,达到更高精度。传统的边缘检测算子,如Sobel算子、Canny算子等对图像边缘的定位只能达到像素级,Zernike矩方法是亚像素边缘检测算子中应用最广泛的方法[3],其定位精度和运行时间均优于其他的空间算子。
本文首先对摄像机进行标定,采用双线定位法找到针脚位置,最后利用基于Zernike矩的亚像素边缘检测算法找到针缘边位置,计算针宽。实验结果表明,该方法检测精度高、效果好。
1 摄像机标定
1.1 畸变参数
实际摄像机的透镜总是在成像仪的边缘位置产生显著的畸变,畸变主要分为径向畸变和切向畸变两种。径向畸变来自于透镜形状的设计,而切向畸变来自于整个摄像机的组装过程中[4]。针对径向畸变,成像仪中心的畸变为0,随着向边缘移动,畸变越来越重,成像仪某点的径向位置可按下式进行调节:
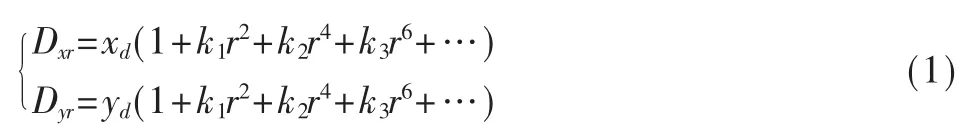
式中,(xd,yd)为畸变点原始位置,(Dxr,Dyr)为矫正后新位置,k1、k2和 k3为径向畸变参数。切向畸变由于装配误差,致使透镜与图像平面不平行,其数学模型为:
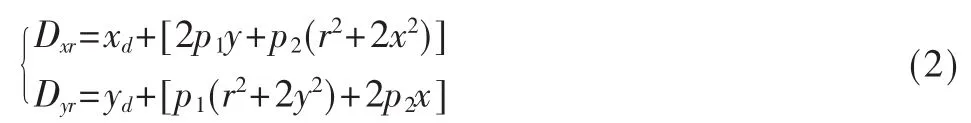
式中,p1和 p2为切向畸变参数。 由此,k1,k2,k3和 p1,p2构成了5个畸变参数,形成一个5×1的矩阵的畸变向量。
1.2 像素当量
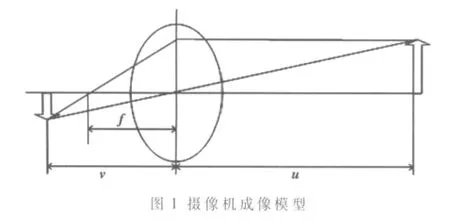
本文方法采用定焦镜头,焦距为定值。根据图1所示的摄像机成像模型可以得到:

其中,u为物距;v为像距;l为物像距离;f为焦距。
设摄像机的像元尺寸为dxmm,则像素当量的表达式为:

2 双线定位法
双线定位法是一种快速、准确的定位方法,两条直线相互垂直。如果在图像某一位置设定一条横线,直线与物体交于点 A(x,y),则垂线必经过点 B(x+d,y),与图像交于点 C(m,n),由此可确定点 D(x,n)。不难看出,当物体在图像中的位置发生变化时,点D(x,n)与图像中物体的相对位置不发生改变,由此可通过平移等方法,确定ROI区域。
3 Zernike矩的亚像素边缘检测
3.1 Zernike矩的定义
Zernike矩的核是定义在极坐标中、单位圆内、正交的 Zernike多项式,图像 f(x,y)的 n阶 m次 Zernike矩定义为[5]:
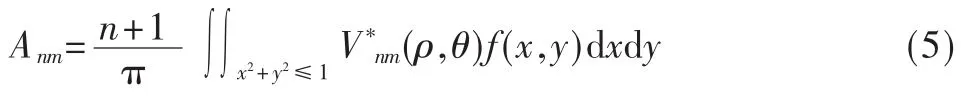
3.2 Zernike亚像素边缘检测
Zernike矩检测边缘基本思想是,通过计算每个像素点的4个参数来判断其是否为边缘点[6]。如图2所示,4个参数分别为 k、h、l和 φ,其中,k为图像边缘阶跃灰度的高度,h标识背景灰度的高度,l为圆盘中心离图像边缘阶跃的垂直距离,圆心与图像边缘阶跃的垂线与x轴所成的角度记为φ,利用Zernike正交矩阵的性质得出旋转前的Zernike矩阵和旋转后的Zernike矩之间的关系式:


利用旋转后的矩 A00、A11和 A20,可得到理想边缘模型的边缘参数为:
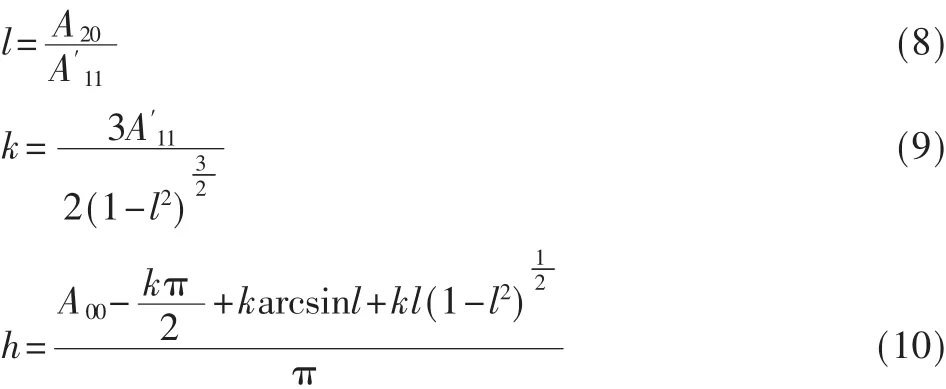
4 小型连接件针宽测量实现
本文采用摄像机标定技术来矫正图像畸变,双线定位法用于快速定位RIO区域(即针脚区域),其他区域不做处理。应用Zernike矩进行亚像素边缘检测和针宽的测量,具体实现步骤如下:
(1)摄像机标定。利用摄像机标定获取摄像机畸变参数,矫正目标图片,根据相机拍摄标定板图片获得像素当量。
(2)针脚定位。采用双线定位法定位针脚位置,只对ROI区域做有效的计算和处理,大大加快了运行效率。
(3)使用Zernike矩进行亚像素级别的边缘检测,并记录边缘点坐标进行距离测量。
5 实验和结果分析
本文选取4×25的标准棋盘格图为标定的目标,棋盘格子的宽度为0.1 cm。根据不同的距离和角度,选取16幅656×492像素的图像作为标定用途。采用间距为0.2 cm的标定板获取像素当量。小型连接件理想针宽为0.03 cm。标定后得到的畸变参数矩阵为:

如图3所示,双线定位法确定红色ROI区域,第一点坐标为(55.14,122.00),第二点坐标为(82.00,53.67),由此确定坐标(55.14,53.67)为相对坐标点,根据此坐标点确定ROI区域。图4为运用Sobel算子进行边缘检测,图5为Zernike矩亚像素边缘检测。
针宽可有下式计算得出:

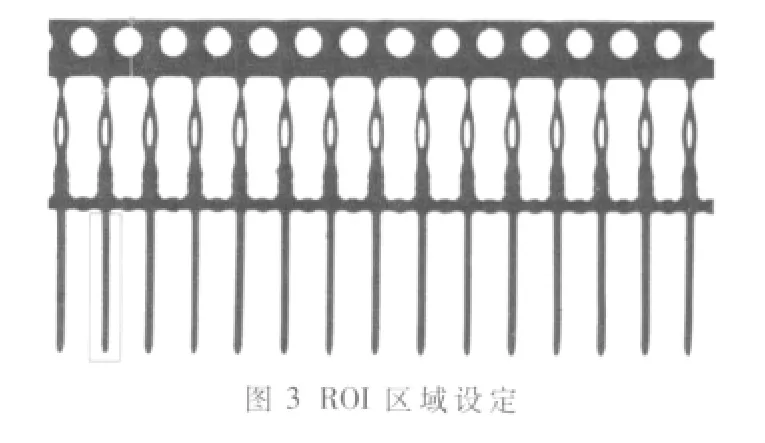

其中,xi为左侧边缘点横坐标,为xi同纵坐标下右侧边缘点横坐标。
根据标定图像可得每33.6个像素对应实际距离为0.2cm,计算结果见表1。
通过实验分析和比较结果表明,通过摄像机标定可以有效地消除摄像头畸变,为后续尺寸测量精度提供保障,而且基于Zernike矩的亚像素边缘检测方法不仅提高了边缘检测的精度,同时也缩小了尺寸检测中的误差。
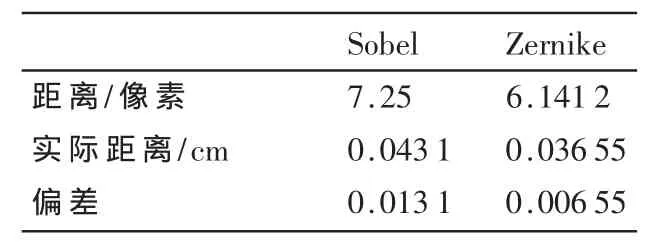
表1 Sobel算子和Zernike矩检测结果对比
[1]李文涛.基于两步法的摄像机标定[J].控制工程,2011,9(18):48-51.
[2]高俊钗,雷志勇,王泽民.高精度测量的相机标定[J].电光与控制,2011,18(2):93-96.
[3]韩丽燕,陈方林.一种Zernike矩亚像素边缘检测的优化算法[J].电子测 试,2010,6(6):1-5.
[4]李明金,熊显名,张绍兵.一种基于Opencv的摄像机标定新方法[J].激光与光电子学进展,2009(12):99-102.
[5]马艳娥,高磊,吕晶晶.基于改进的Canny算子和 Zernike矩的亚像素边缘检测方法[J].电子测试,2011,7(7):20-23.
[6]PAPAKOSTAS G A,BOUTALIS Y S.Numerical error analysis in Zernike moments computation[J].Image of Computer Vision,2006,24(9):960-969.
