雷击地线档距中央的反击性能分析

2012-07-03周志成陶风波陈少波

电力工程技术 2012年6期

周志成，马勇，陶风波，陈少波，魏旭

(江苏省电力公司电力科学研究院，江苏南京 211103)

雷击是造成输电线路故障跳闸的主要原因，雷击主要分为反击和绕击，其中反击主要是强雷雷击塔顶及其附近地线引起绝缘子串闪络造成[1]。近年来，超高压输电线路高杆塔、大档距、交叉跨越、同塔多回、导线换相等情况普遍出现，雷击地线档距中央造成反击跳闸、地线断线等事故逐渐增多。

1 雷击分析理论

1.1 绝缘闪络判据

1.1.1 规程法

规程法是比较绝缘子串两端出现的过电压与绝缘子串或空气间隙50%放电电压方法作为判据，过电压超过绝缘的50%放电电压即判为闪络[2]。国内外运行经验表明规程法计算结果导致线路跳闸率明显偏高[3]，目前线路防雷计算中主要采用相交法和先导法。

1.1.2 相交法

相交法是只要绝缘子串上的过电压波与伏秒特性曲线相交，即发生闪络，不相交就不闪络。伏秒特性满足：

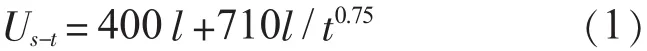
式（1）中：Us-t为绝缘闪络电压，kV；l为绝缘距离，m；t为从雷击开始到绝缘闪络所经历的时间，us。

对于 50%击穿电压，t取 10 us，代入式（1），即：

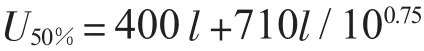
1.1.3 先导法

由于作用在线路绝缘上的雷电过电压并非都是标准波形，其闪烙不完全满足伏秒特性规律，故提出利用先导发展模型法作为绝缘闪络的判断依据[4]，即当线路绝缘上电压出现的时间达到一定的流注发展时间Ts值时，先导开始发展，其速度随施加的瞬时电压与剩余间隙长度而变，当流注占满整个间隙长度d时，绝缘闪络。该方法理论上比较符合放电物理过程，但先导法的有关参数通过长空气间隙放电试验得出，其分散性会影响计算准确性[4]。由长空气间隙放电研究得知，间隙击穿时间Tb由流注起始时间Tp、流注发展时间 Ts、游离波传播时间Ti、先导发展时间TL、气体加热时间Tg组成，近似取：

据实验数据得出Ts与先导发展速度v1的经验公式[3]：

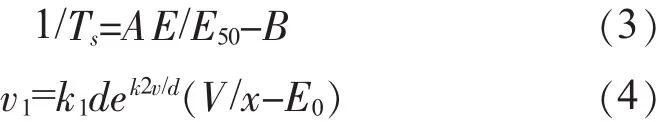
式（3，4）中：E 为闪络前最大平均场强，kV/m；E50为50%放电电压下的平均场强，kV/m；E0为先导发展的阈值场强，kV/m；A，B为由间隙类型及电压极性决定的实验常数，分别取 1.25 和 0.95[5，6]；v1为先导发展速度，V/m；d为间隙长度，m；V 为瞬时电压，kV；x为剩余间隙长度，m；k1和k2为与绝缘性质、电压极性等有关，分别取170和1.5×10-3[6]。

1.2 雷击计算模型

以220kV典型线路模型为例，受击线路左右两边杆塔分别为ZTS-32.7、全高44.7 m，和FTSS3-27（双回路）、全高44.5 m，全线架设2根地线。如图1所示，因雷电流作用时间较短，为避免雷电流波折反射对雷击点的影响，雷击档距两侧各增加2个档距，并在线路终端增加10 km长线路[7]。架空输电线路采用频率相关模型（Frequency Dependent（Phase）），相关参数如表1所示。输电线路杆塔采用传输线波阻抗（多波阻抗）模型[8-12]，接地电阻为2 Ω。雷电通道采用一个受控的雷电流源与雷电通道波阻抗并联等效，雷电通道波阻抗取400 Ω[4]。

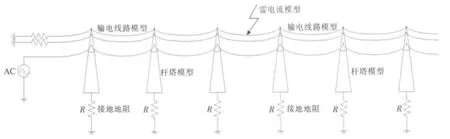
图1 仿真模型示意图

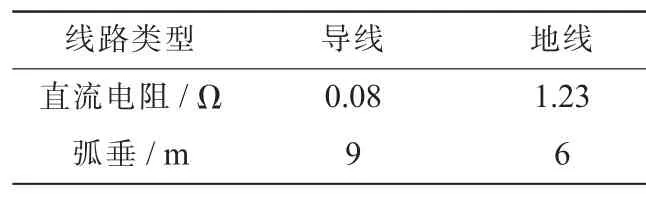
表1 线路相关参数

2 仿真分析

分别从雷电流幅值I、雷击点位置s（s为雷击点与指定一侧杆塔间的距离）和档距L 3个因素考虑对线路反击耐雷水平的影响[13]。

2.1 档距中央的反击耐雷水平分析

当线路档距为420 m和200 m时，分别模拟雷电流幅值大小为 75 kA，100 kA，125 kA，150 kA 和200 kA，采用先导法计算雷击中档距中央地线的反击耐雷水平，如图2所示。其横坐标为雷电流幅值I，纵坐标为雷击点地线与B相导线之间的电压U，虚线以上几种情况空气绝缘发生闪络。由图2可知，雷电流越大，地线与导线间电压差越大，当雷击点电压大于间隙击穿电压时，就会发生空气绝缘闪络。

2.2 雷击点对反击耐雷水平的影响

档距为420 m和200 m时，雷击档距中央地线和导线间的电压U与雷击点s的关系如图3所示。虚线以上几种情况空气绝缘发生闪络。

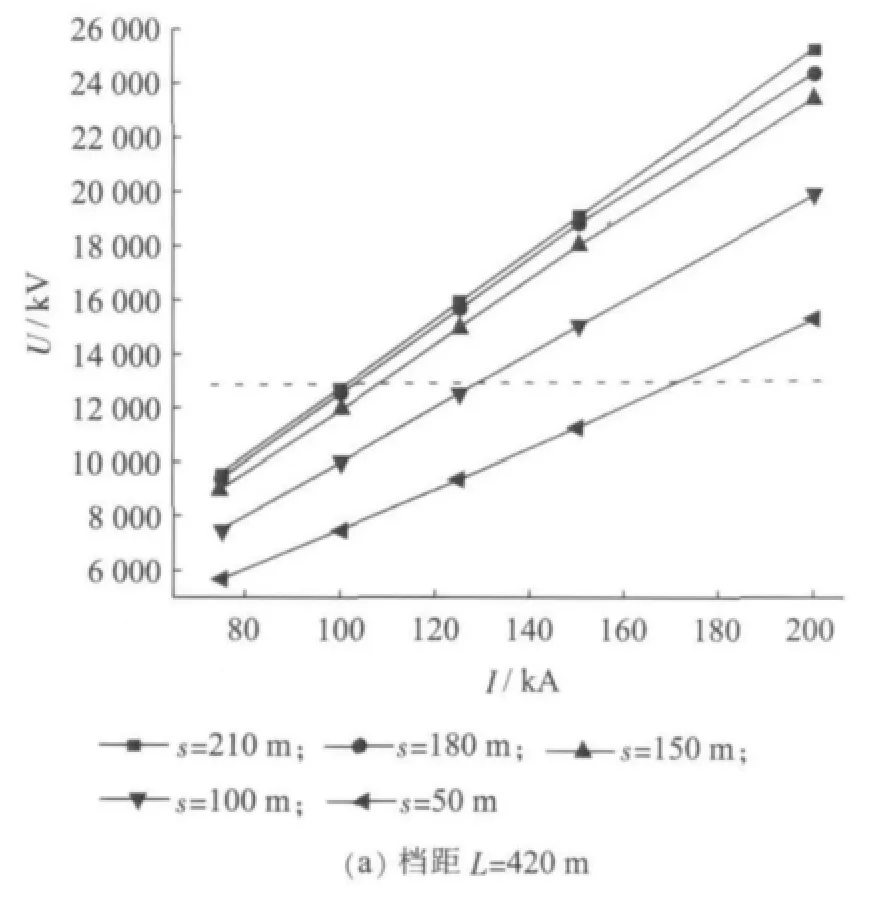
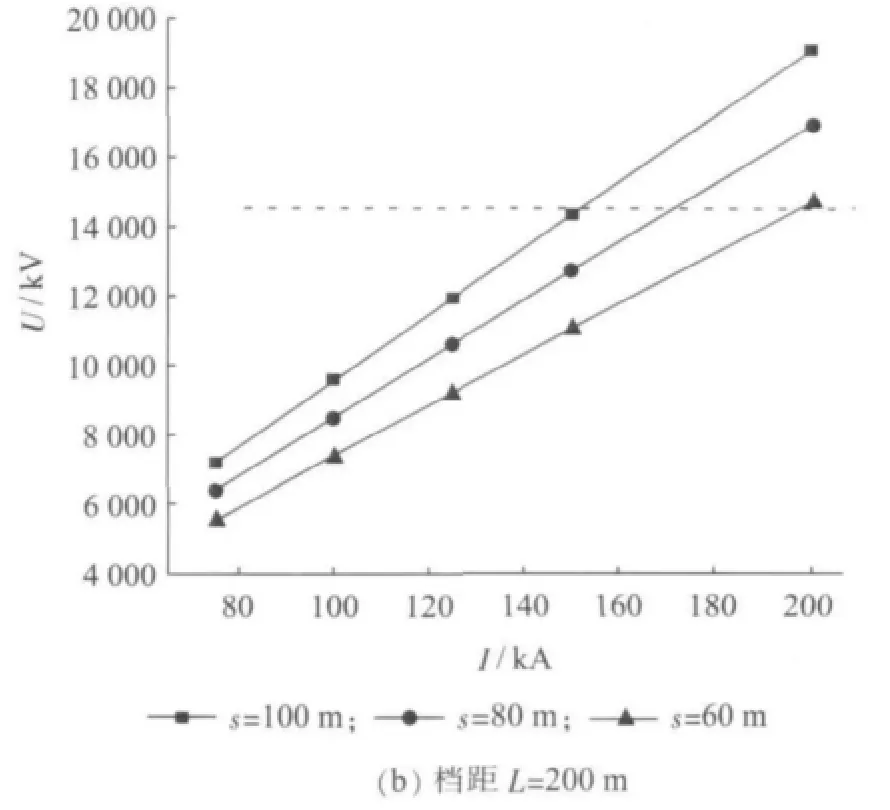
图2 雷击档距中央地线和导线间电压与雷电流大小关系

从图3中可以看出，相同雷电流下，雷击点越靠近杆塔（即s越小），地线与导线间的电压U越小，当雷击点位于档距正中间附近时变化时，电压U变化不大。同样条件下，雷击地线档距正中央，地线与导线的电压差最大，雷击点电位较高。因为雷击档距中央时，雷电波分别沿线路向两边的杆塔传播，此时传播至杆塔的距离最长，杆塔反射来的负雷电波所需时间较大，雷击点易形成高电压。而雷击点位于杆塔附近时，杆塔快速反射回来的负雷电波会削弱雷击点电压。

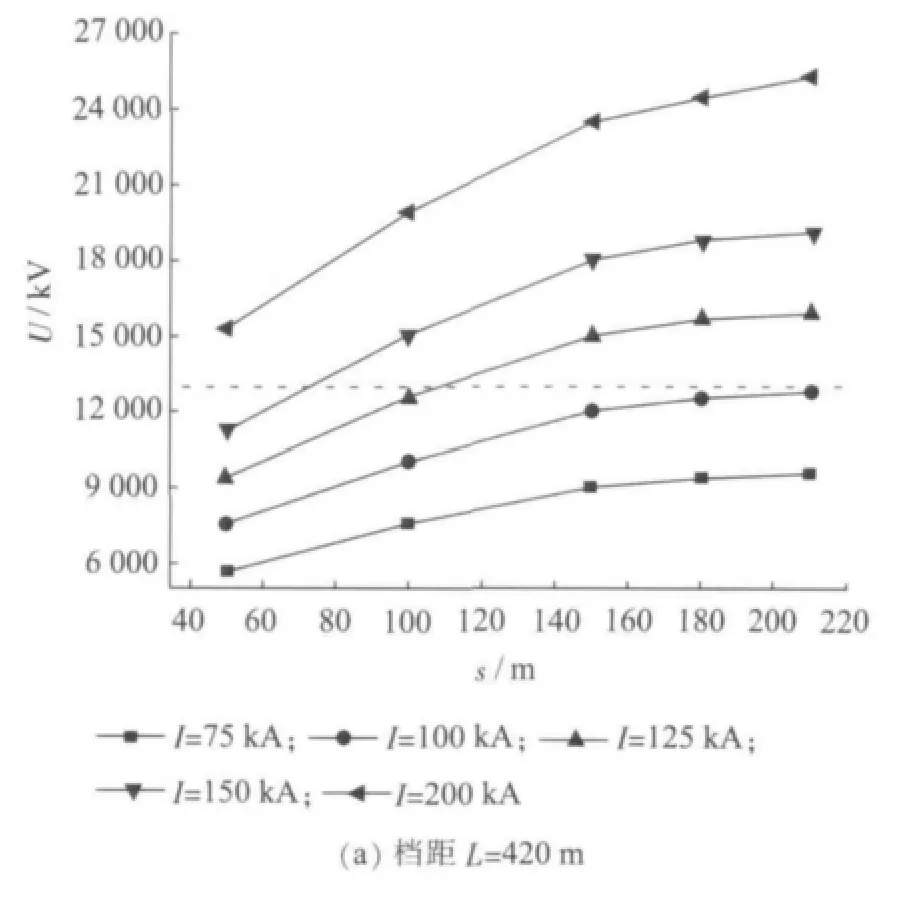
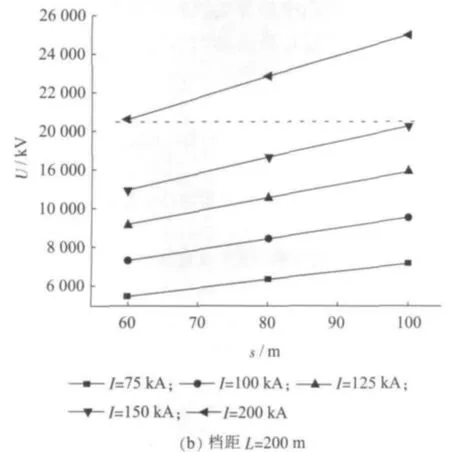
图3 雷击档距中央地线和导线间的电压与雷击点的关系

2.3 档距大小对反击耐雷水平的影响

雷击点位于档距1/2和1/3处时，线路档距耐雷水平的关系如图4所示。

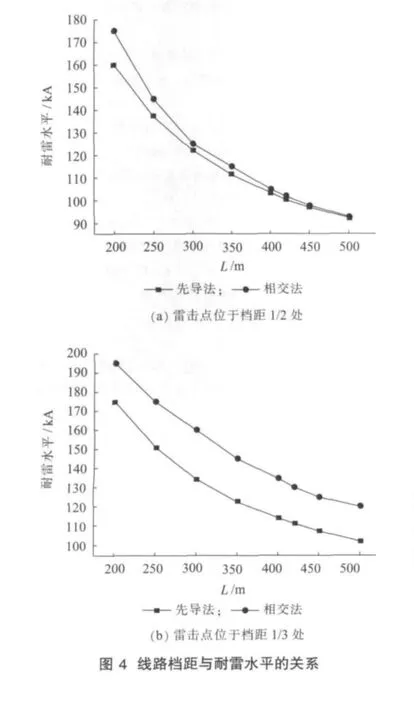
由图4可知，相交法比先导法得到的耐雷水平大，但规律相同，即随着档距增大，耐雷水平逐渐减小，当档距＞350 m时，耐雷水平减小速度变慢。雷击地线档距中央时，雷电波沿地线向两边传播，经两侧杆塔反射的时间随档距大小而不同。档距较小时，雷电波传播至两边杆塔，产生负反射波沿地线快速传播回来，降低雷击点过电压，避免绝缘闪络，提高了耐雷水平；档距增大时，产生的负反射波传播至雷击点的时间加长，雷击点易形成高的过电压，地线与导线间的电压超出绝缘水平时发生闪络，故重雷害区域，线路档距不宜过大，必要时应采取其他措施提高线路耐雷水平[13，14]。

3 雷击地线反击实例分析

某220kV线路7号与8号塔间地线雷击断线，断线点位置距离7号塔约180 m，在导线180 m处发现有电弧烧伤痕迹。7号塔型为ZTS-32.7、全高44.7 m，8号塔型为 FTSS3-27（双回路）、全高 44.5 m，档距420 m。地线为GJ-50镀锌钢绞线（7根单线直径3.0 mm）。地线为2根水平排列，7号、8号塔附近地形平坦，导线交叉换相。

据雷电定位系统查询，该线路落雷雷电流幅值为103.3 kA。利用ATP及PSCAD建立模型仿真，分别用相交法和先导法计算地线与导线之间的闪络判据，如图5、图6所示。图5中地线和导线间的电压波形与伏秒特性曲线刚好相交，图6中12 us左右时，先导发展速度为0，地线和导线上的电压相等，即发生绝缘闪络。2种方法都计算得出该雷击造成了导地线发生闪络，相交法以标准雷电波计算，未考虑杂散参数影响，对避雷器伏秒特性需准确掌握；先导法模拟了雷电先导发展的物理过程，但相关时间参数由经验得出，计算值偏保守。

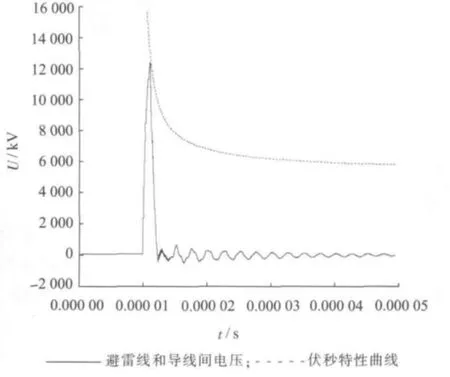
图5 相交法判断地线与导线是否发生闪络

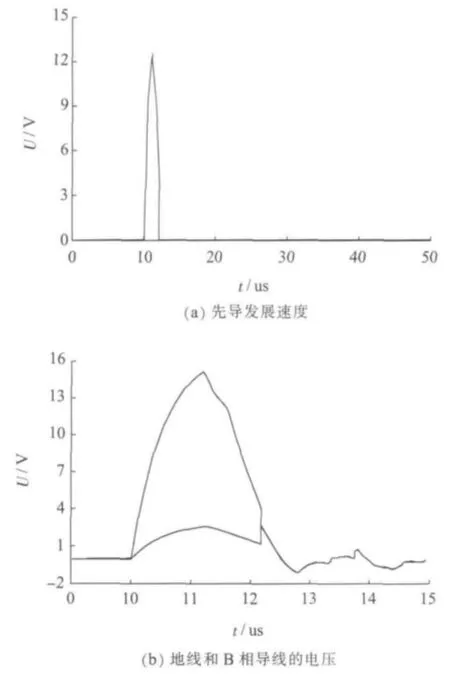
图6 先导法判断地线与导线是否发生闪络

计算结果表明该地线与B相导线之间的最大耐受雷电流约为97.3 kA，故线路在雷电流为103.3 kA、雷击档距中间180 m处时，地线与导线间会发生空气绝缘闪络，其主要原因：（1）7号与8号杆塔较高（约45 m），档距也较大（达 420 m），雷击点易形成高电位；（2）雷击点距离7号塔180 m处，位于档距中央附近，雷击点电压相对较高；（3）该档距进行导线三相的交叉换相，略缩小了B相与地线的间距；（4）雷电流幅值高达103.3 kA，超过雷击档距中央的耐雷水平[15]。