小波帧变换方法在电能质量扰动中的仿真分析

刘 刚，张 杨，李 洁

(1.上海电力学院电力与自动化工程学院，上海 200090;2.中国银联股份有限公司技术管理部，上海 200135)

在三相交流系统中，各相电压和电流的幅值应大小相等，相位对称且相差120°.由于系统中的发电机、变压器和线路等设备非线性或不对称，负荷性质多变，加上调控手段不完善、操作失误、外来干扰和各种故障等原因，这种理想的状态并不存在，因此产生了电网运行、电力设备和供用电环节中的各种问题.由此便产生了电能质量(Power Quality)问题，即导致电压、电流或频率出现偏差，其内容包括频率偏差，电压偏差，电压波动与闪变，三相不平衡，暂时或瞬态过电压，波形畸变(谐波)，电压的暂降、中断、暂升，以及供电不连续等.针对供电、用电系统及其设备正常工作的电压、电流的各种指标偏离规定范围的程度等问题，本文使用小波帧算法结合小波变换方法对多种小波在算法框架上进行了比较，与传统小波变换方法相比，小波帧变换在电能扰动定位的准确度方面有较大的提升，不仅具有平移不变性，而且具有更高的稳定性和可靠性［1］.

1 基于小波变换的算法框架

小波分析是20世纪末发展起来的新兴学科，对非线性科学、网络与信息安全研究有很大的推动作用，其小波框架作为离散小波变换的主体部分更是倍受关注.

早在20世纪末，MALLAT将计算机领域中的多分辨率思想引入小波变换中，提出多分辨率分析理论，给出了类似于快速Fourier变换的小波算法——Mallat算法［2］.该算法具有设计简单，预算快速的特点.本文针对利用a尺度正交小波分解信号，其改进的Mallat算法可以获得更好的分辨率，并且比小波包分解效率更高，只是需要保证计算量要和2尺度小波相同.下面给出a(a∈Z+，a≥2)尺度正交小波的Mallat算法.

假设f(x)的近似函数fm(x)∈Vm，对于尺度空间有如下关系:

2 小波框架

由DUFFIN和SCJAEFFER最早在由非正则样本值{f(tn)}n∈Z重构带限信号f时提出了小波框架理论［3］.

序列{φn}n∈Γ是 Hilbert空间 H 中框架，若存在两个常数0＜A，B＜∞，使得对∀f∈H，有:

在此条件下，H空间的向量f能够从它和一族向量{φn}n∈Γ进行内积重构，指标集Γ可以为有限或无限［4］.

连续小波变换的定义如下.

对于一个ψ(t)∈L2(R)，且

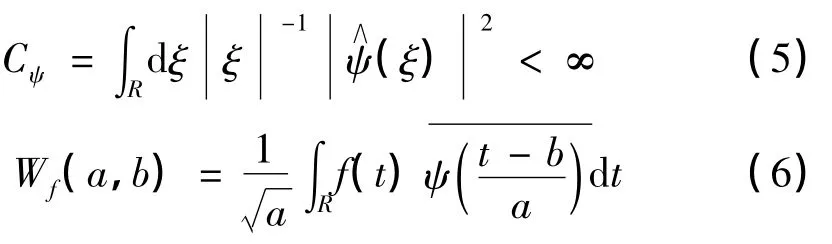
称ψ(t)为小波函数.

式中:a——尺度系数;

b——平移系数.

在式(6)中，若令 a=a0j，b=kb0a0j，j，k∈Z，a0＞1，b0＞0，可得到离散小波变换:

其中，ψ，a0，b0可作灵活选择，ψj，k可构成 L2(R)的正交基，但是满足正交、紧支、对称的小波只有Haar小波.

在放宽正交、线性无关条件的情况下，同时也要获得从 ＜ f，ψj，k＞ 构造 f(t)∈L2(R)的数值稳定的重构算法，要求 ψj，k能构成框架，称为小波框架［5］.具体构造小波框架时，可以通过对一个连续小波变换的时间参数和尺度参数采样来实现，需要利用相应的离散小波序列Heisenberg信号箱去覆盖时频平面［6］.小波 ψu，s在时间上的分布主要集中在和s成正比的区间域U中，在和1/s成正比的频率范围中，其傅里叶变换ψu，s有以频率η/s为中心的支集.为了要获得完全覆盖，可以利用足够小的伸缩步长a＞1，在指数序列{aj}j∈Z中采样，时间平移U在尺度aj成正比的间隔上均匀采样，得到:

按照比例 s=aj伸缩变换的小波 ψn，i的Heisenberg盒子有分别和aj和a－j成正比的时间和频率宽度，保证 ψ，a，u0满足一定的条件，{ ψj，n}(j，n)∈Z2则可成为 L(R)的框架，若 u0和 a足够小，时间频率平面由这些盒子所覆盖，则称小波框架是稳定的［7］.

3 小波帧算法和小波变换算法比较

由于自身变换中的抽样过程，小波变换不具有平移不变的特性，即当输入信号发生整数平移时，会引起小波分解系数的较大变化;小波帧变换由于没有抽样过程，具有平移不变特性，更有利于信号的分解与重构.本文在分析小波变换的基础上，提出了小波帧变换，并探讨了基于小波帧变换的电能质量扰动的时间定位，在准确性方面获得了满意的效果.小波帧变换的每一尺度层均有一冗余信息，因此其在实时性方面略有欠缺.

小波帧变换的原理如图1所示.

图1 小波帧变换原理

小波帧变换处理图像整合问题时，通常需要进行配准.配准是指同一区域内以不同成像手段所获得的不同图像和图形的地理坐标的匹配，包括几何纠正、投影变换，以及统一比例尺等3方面的处理.对于多信息的复合综合分析时常需进行各种配准处理，本文将小波帧变换用于电能质量信号的处理主要是针对扰动起止时刻的定位，不存在几何纠正、投影变换和统一比例尺度等问题，因此不需要配准处理.

常用的小波有如下几种:Haar小波是紧支撑但不是连续可微的，应用有限，多用于理论研究;Morlet小波是复值小波，能够提取信号中的幅值和相位信息，但是没有尺度函数，而且为非正交分解;Mexico草帽小波是实值小波，该小波无尺度函数，主要用于信号处理和边缘检测，为非正交分解;Meyer小波不是紧支撑的;Daubechies小波是离散正交小波，简称dbN小波，N是小波的阶数，N越高其正则性条件越好，即相应的基本小波频域上有较好的局域性能，具有不对称性;Symlet小波性质和 dbN小波相似，但更近于对称小波;Coiflet小波性质和Symlet小波类似;biorNr.Nd小波是双正交小波，虽然解决了正交性与现行相位要求的矛盾，但不具有紧支撑正交.

本文选用db4小波作为母小波对电能质量问题进行大量的仿真实验，并以电压暂升、电压暂降、电压中断、脉冲振荡为例进行说明，分别利用小波变换和小波帧变换进行定位.具体见图2，图3，图4 和图5.

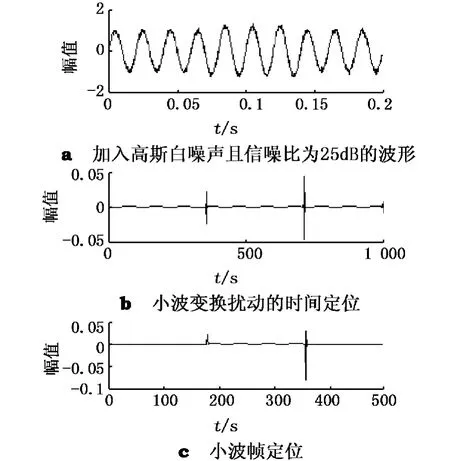
图2 小波变换与小波帧变换对电压暂升定位

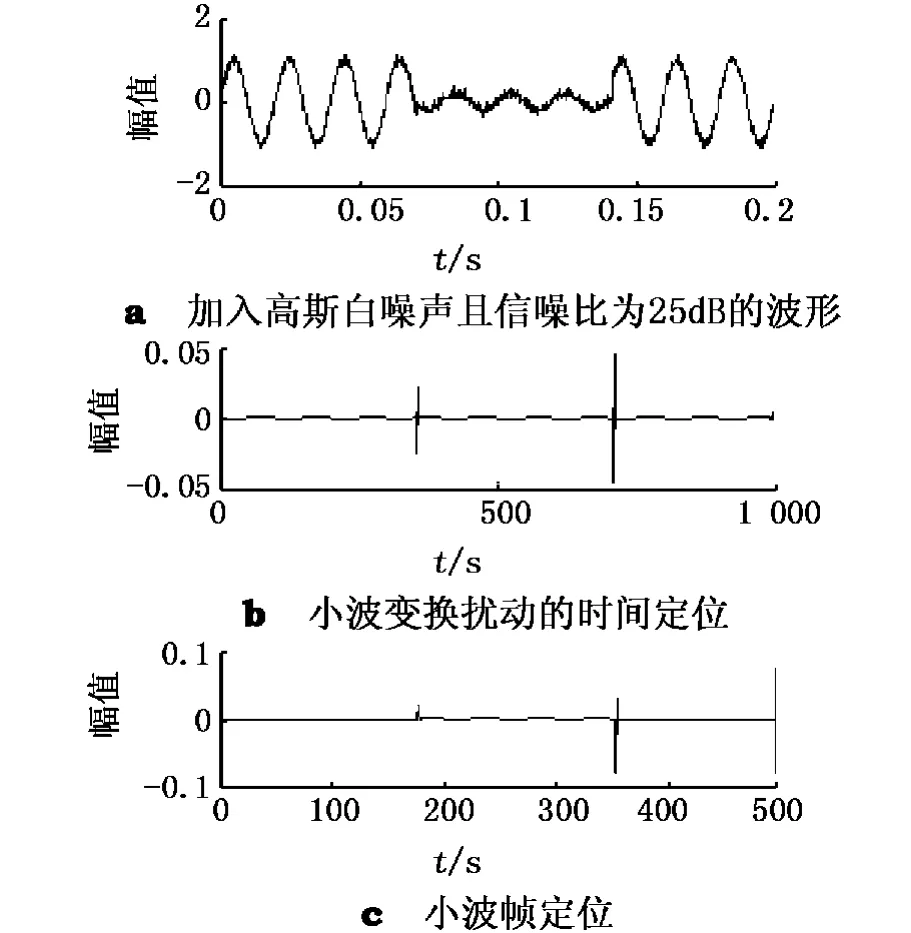
图3 小波变换与小波帧变换对电压暂降定位

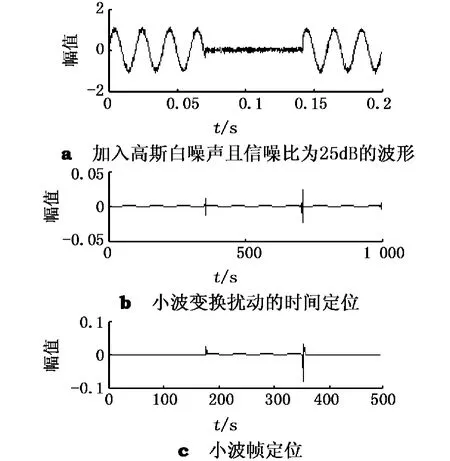
图4 小波变换与小波帧变换对电压中断定位

图5 小波变换与小波帧变换对脉冲振荡定位

仿真实验证明，基于小波帧的算法在牺牲了实时性的同时，在扰动时间定位的准确性方面有很大提升.

4 结语

本文首先提出了一种基于小波变换的电能扰动分析的算法框架，并在此基础上提出了基于小波帧的算法.相对于小波变换而言，小波帧变换由于没有抽样过程，具有平移不变特性，更有利于信号的分解与重构.通过大量实验对两种变换进行比较后，得出了基于小波帧的算法在电能质量扰动的时间定位的准确性方面有很大提升、并具有一定实用性和有效性的结论.

［1］董卫军.基于小波变换的图像处理技术研究［D］.西安:西北大学，2006.

［2］陶冰洁，王敬儒.采用小波分析的图像融合方法评述［J］.计算机工程与应用，2005，25(7):6-19.

［3］佘泽红.小波框架的理论与应用［D］.西安:陕西师范大学，2006.

［4］彭景林.基于互信息和离散小波帧分解的医学图像配准研究［D］.长沙:湖南大学，2006.

［5］孙鑫，谢元旦，任地成.基于小波变换和子图的图像配准方法［J］.计算机工程与设计，2010，31(21):4 653-4 656.

［6］LUO Hai.Grid harmonic harm and suppressing［J］.Inner Mongolia Technology and Economic，2008，3(1):2-6.

［7］DAUBECHIES I，SWELDENS W.Factoring wavelet transforms into lifting steps［J］.Fourier Anal，1998，14(4):247-269.