基于小波分析水轮机导叶开度的自适应控制研究

2012-07-02曾繁玲

大电机技术 2012年3期

曾繁玲

（广东省罗定职业技术学院，广东云浮 527200）

引言

水轮机导叶开度的控制是一个非线性模型，对水轮机导叶进行实时地控制，能够确保水轮机组的动力矩和阻力矩处于平衡状态，进而可以使水轮机的机组转速和输出频率处于一定的稳定范围内。因此，对水轮机导叶开度进行有效控制是提高水轮机机组运行稳定性的关键所在。目前，许多科学家提出了很多水轮机导叶开度的控制方法，比如，基于微分几何的反馈线性化方法是一种较好的鲁棒控制方法，对水轮机导叶控制具有很好的控制效果，但是控制系统的精确数学模型很难建立，同时参数的改变影响控制系统的鲁棒性难以解决。因此，应该寻求一种能够具有简单、易于实现等鲁棒性好的控制方法对水轮机导叶进行非线性自适应控制。

小波分析是傅立叶变换方法的提升，已经得到了广大科学家的关注，并且已经成功地应用于解决多种工程实际问题之中。小波分析具有多分辨分析的优点，能够在时域和频域内具有较好的局部化能力，还对控制对象的细节进行分析，信号的相位变化可以较容易地被觉察到，能够提出调制信号中的瞬时特征。因此，利用小波分析的时频分析的优势，对水轮机导叶进行自适应控制是一种行之有效的方法。

1 水轮机导叶开度的数学模型

（1）水轮机导叶开度开机的数学模型

（a）上升阶段：导叶开度在 18s内从 0提高到18%，相应的导叶开度上升数学模型如下所示：

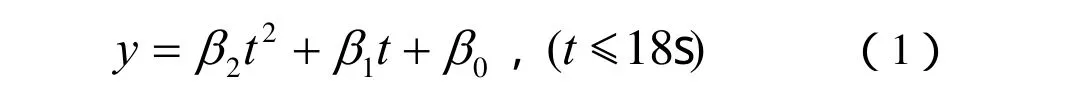
式中，2β、1β和0β均为常数。

上升阶段有6s的振荡阶段，振荡的数学模式可以表示为如下的形式：

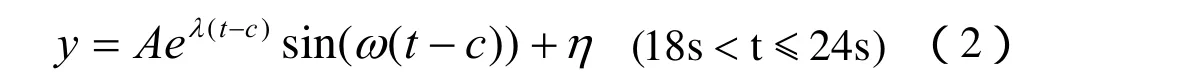
式中，A——衰减振幅；

λ——衰减率；

ω——频率；

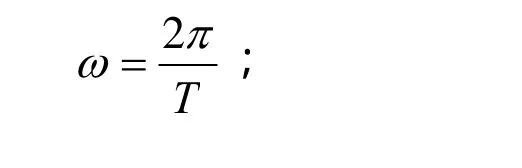
T——周期；

C——相位；

η——稳态的水轮机导叶开度。

（b）平稳阶段一：导叶开度在10s内一直稳定在18%，相应的数学模型为：

（c）有功上升阶段：导叶开度在76s内从18%到达最大极限98%，相应的数学模型表示为如下的形式：

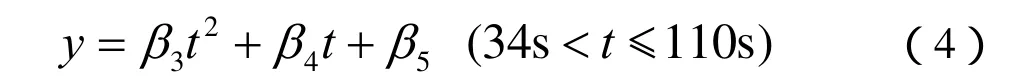
式中，3β、4β和5β均为常数。

（d）最大开度振荡衰减阶段：导叶开度达到了96%，再经过 10s水轮机导叶稳定在 98%，相应的数学模型如下所示：

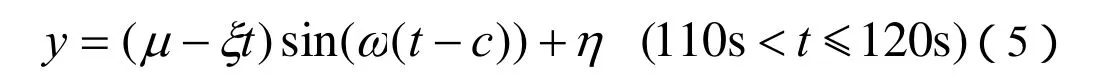
式中：µ——常数；

ξ——衰减幅度；

T——周期；

c——相位；

η——稳态的水轮机导叶开度。

（2）水轮机导叶开度关机时的数学模型

（a）甩负荷下降阶段的数学模型如下所示：

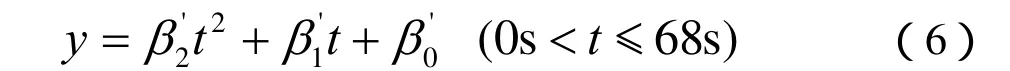
（b）甩符负荷振荡阶段的数学模型如下所示：

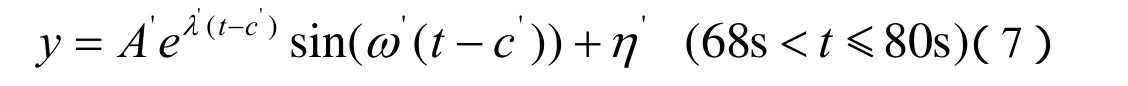
（c）稳定阶段的数学模型如下所示：

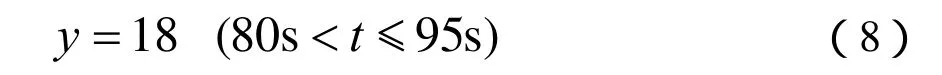
（d）空载阶段的数学模式如下所示：

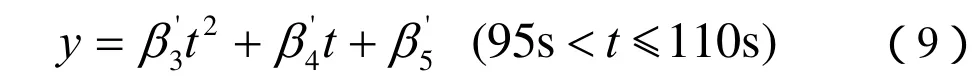
（e）空载振荡阶段，相应的数学模型如下所示：

（3）水轮机导叶开度的非线性控制模型

水轮机导叶开度的非线性控制的数学模型如下所示：

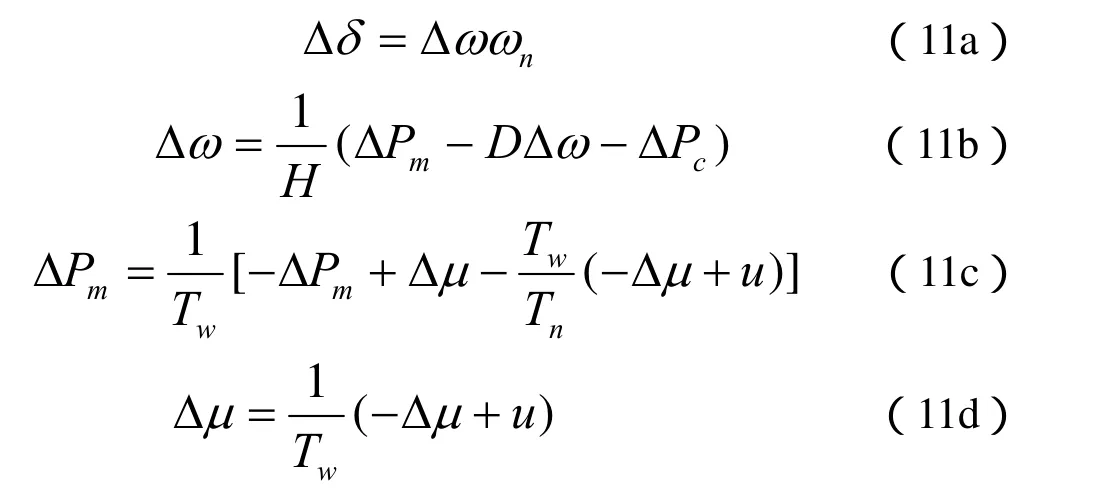
式中：Δω——水轮机导叶旋转角速的偏差；

H——水轮机的扬程；

D——水轮机导叶的外径；

ΔPc——水轮机水利效率的偏差；

u——水轮机导叶随动装置的输入信号。

式（11）可以进一步地转换为矩阵形式，如下所示：

式中：

2 小波多分辨分析

由于水轮机导叶开度的变化具有不稳定的特点，因此，可以利用具有时频分析优势的小波分析对该非稳定信号进行分析。

（1）小波分析的基本理论

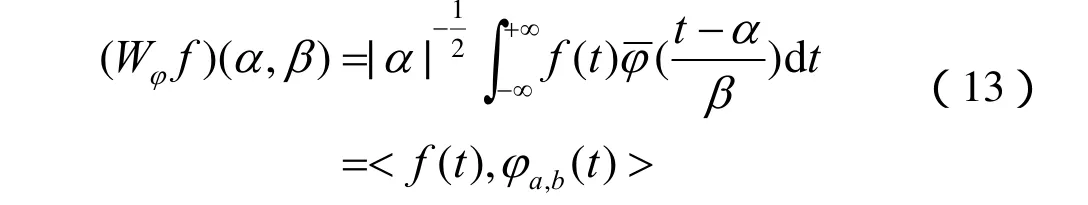
α——伸缩因子；

β——平移因子；

（2）小波分析多分辨分析的特征

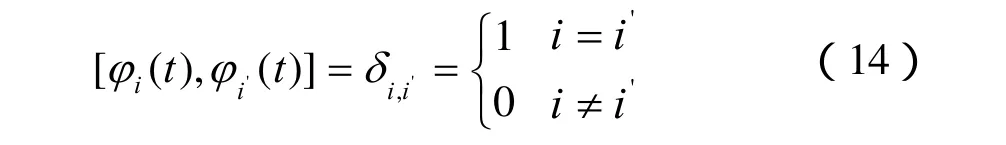
那么，ϕ(t)为尺度函数，其中V0称为尺度空间，可以表示为如下的形式：

对尺度函数进行平移和伸缩可以获得一个尺度函数集，可以表示为如下的形式：

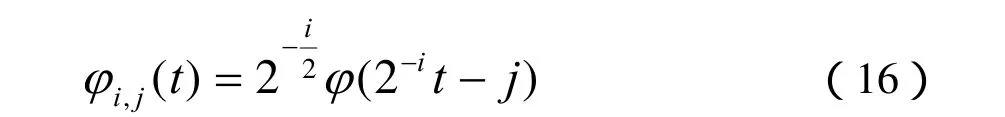
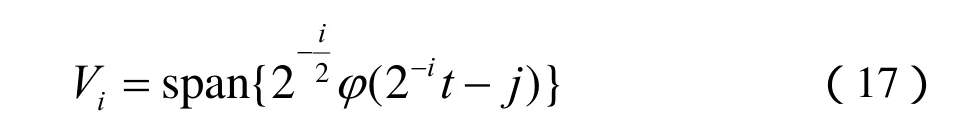
对于任意信号函数都可以进行如下的小波变换：

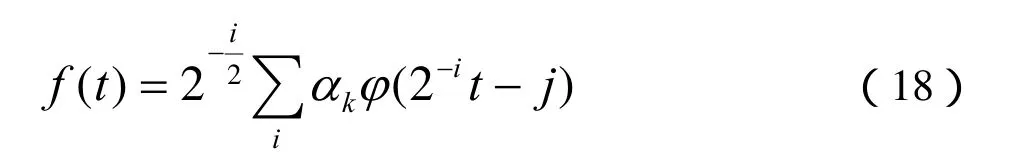
尺度函数可以张成尺度空间，随着尺度的不断变大，尺度函数所平移的间隔也随之增加。反之，张成的尺度空间能够确定信号的细节。因此，尺度的变化可以实现信号分析的精度大小，也就是小波分析的多分辨分析，可以通过如下的表达式来表示：式中：W1表示细节空间；V1表示大尺度逼近空间；在进行信号控制时可以根据实际情况，将尺度空间进行分解，从而获得细节信号和尺度信号。

（3）小波函数的确定

Gauss函数满足式（11），因此基于小波分析的水轮机导叶开度控制可以选择Gauss函数，在尺度i的条件下其数学表达式如下所示：Gauss函数时频窗口的宽度随着尺度的上升而变宽，随尺度的降低而增加。

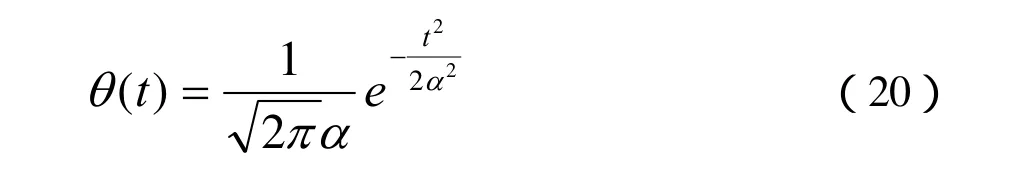
（4）水轮机导叶开度信号的小波分析

利用小波分析将水轮机导叶开度信号进行分解，利用不同的阈值在不同尺度上将噪音消除，然后对信号进行重构，进而能够提高控制的精度。

通过测试获得水轮机导叶开度信号后，利用Mallat算法对其进行N层尺度分解，进而获得N组细节信号，（i=1,2,…,N）和平滑信号li。利用软阈值和硬阈值消除噪声，相应的数学表达式如下所示：

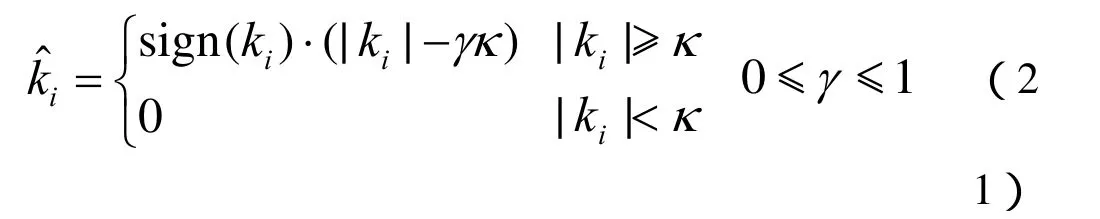
3 水轮机导叶开度的控制仿真

基于小波分析水轮机导叶开度自适应控制的控制系统结构简图如图1所示。

图1 基于小波分析的水轮机导叶开度控制系统结构简图

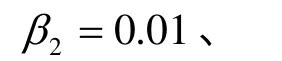
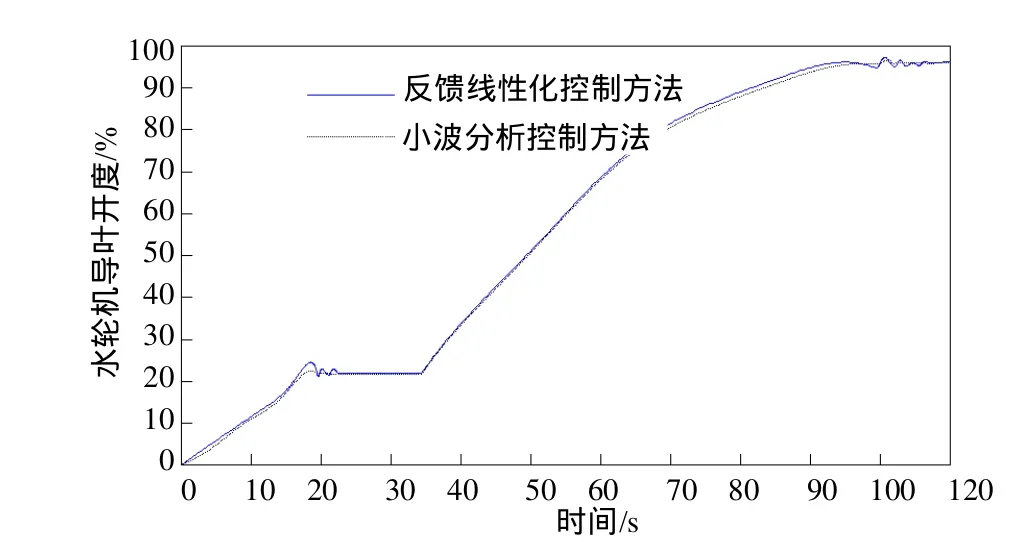
图2 水轮机导叶开度开机过程仿真曲线对比图

图2给出了分别利用反馈线性化控制方法和小波分析控制方法对水轮机导叶开机时的开度进行控制的仿真曲线，从图中可以看出，开机时水轮机18～24s，以及100～110s的时间段内有一段振荡阶段，利用反馈线性化控制方法所获得的仿真曲线在该振荡时间内有较大的超调节量，并且进入稳定状态所花费的时间较长，响应速度较低，而利用小波分析控制方法进行控制仿真的曲线在振荡段内几乎没有超调，并且响应时间比较短，说明该小波分析控制方法具有更好的控制效果。

图3给出了分别利用两种控制方法对水轮机导叶开度在关机阶段进行控制的仿真曲线，从图中可以看出，在关机阶段水轮机导叶的开度变化曲线在68～80s之间以及100～110s之间有两个振荡阶段，利用反馈线性化控制方法所获得控制仿真曲线在振荡段响应时间比较短，具有较大的超调量；而利用小波分析控制方法时控制仿真曲线的振荡段较快地进入稳定阶段，并且几乎没有超调量，因此，小波分析控制方法具有更好的控制精度和控制稳定性。