多目标规划的LINGO求解法

吴有平，刘 杰，何 杰

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.湖南省建筑工程集团总公司，湖南 长沙 410004）

0 引言

多目标规划（multiple objectives programming）是数学规划的一个分支，它研究多个目标函数在给定区域上的最优化问题，又称多目标最优化。19世纪末法国经济学家V.Pareto[1]最早研究了不可比较目标的优化问题，之后J.V.Neumann等人[2]做了较深入的研究。多目标规划的研究越来越受到人们的重视，但至今有些理论问题尚在探讨之中，其求解方法也在不断改进。

求解多目标规划问题的方法主要有2类：一是化多为少的方法，即把多目标化为较容易求解的单目标或双目标，如主要目标法、线性加权法、平方和加权法、理想点法等。二是分层序列法，即把目标按其重要性给出一个序列，每次都在前一目标的最优解集内求下一个目标的最优解，直到求出共同的最优解。除了上述2类外，还有修正单纯形法和层次分析法。层次分析法，由T.L.Saaty[3]于20世纪70年代提出，是一种定性与定量相结合的多目标决策与分析方法，对于目标结构复杂且缺乏必要数据的情况较实用。

LINGO（linear interactive and general optimizer）是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件包。LINGO也是一种最优化问题的建模语言，有许多常用的函数供使用者建模时调用，还提供了与其它数据文件的接口，易于方便地输入、求解和分析大规模最优化问题。本文采用LINGO软件（9.0版）求解多目标规划转化后的单目标规划问题。

1 模型的一般表达式

求x=(x1,x2,…,xn)，使模型的理想目标达到极大或极小，同时满足模型的现实目标和硬约束的要求，其数学表达式为：

理想目标

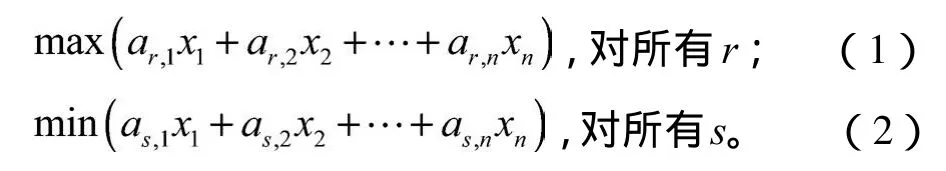
现实目标和硬约束

式（1）～（3）中：r =0,1,…，是极大化理想目标个数；

s=0,1,…，是极小化理想目标个数；

t=0,1,…，是现实目标和刚性约束个数；

*表示<，=或>。

在某些情况下，对决策变量的非负约束（4）可能不满足，即存在决策变量取负值的情况[4]。

对每个目标函数确定一个希望达到的期望值就是理想目标，由于受各种条件的限制，这些目标值往往不能全部都达到，现实中要达到的数值b就是现实目标。约束跟现实目标的表达形式相同，但现实目标是弹性的，而约束是绝对的。因此，当一个现实目标必须满足时，就称它为硬约束。

2 建立LINGO模型的步骤

1）选定设计变量。多目标规划中，要求确定的未知量可用一组基本参数来表示，这些基本参数可以是常量也可以是变量。变量的选取是在求解模型过程中不断优化变更的，因此也称为设计变量，可用一个向量x=(x1,x2,…,xn)表示。

2）确立目标函数。理想目标由决策变量的数学函数（目标函数）表达，目标函数表示决策者的某种愿望，如最大利润或最小成本等，其表达式可能是线性的也可能是非线性的，用max f(x)或min f(x)表示。现实目标就是理想目标和某一指标值相配合（也就是配上右端项），构成的决策变量的数学函数，称为现实目标，用g(x)=b，g(x)b表示。

3）建立约束条件。约束跟现实目标的表达形式相似，只是在求解模型时必须满足其条件。LINGO优化软件的不同版本对约束个数有不同的限定，例如：工业版本最大约束数为16 000，Demo（demonstration）版本最大约束数为150。

4）数学模型。就是对决策问题用数学表达式来描述。用LINGO软件求解多目标规划时，理想目标只能有1个，其他的理想目标需要根据目标满足的优先级别转换成现实目标或约束。形式如下：

3 应用举例

例1 用3种不同的原液M1，M2，M3配制成3种饮料D1，D2，D3。已知每天有1 500 L的M1，每升6.00元；有2 100 L的M2，每升4.50元；有950 L的M3，每升3.00元。已知配方如下：D1由不到10%的M2和超过50%的M1配成，每升售价6.00元；D2由不到60%的M3和超过10%的M2配成，每升售价5.50元；D3由不到50%的M3和超过50%的M2配成，每升售价5.00元。首先要保证产品质量，其次是要求每天生产2 000 L的D1。怎样安排生产才能使利润最大[5]。

解 1）设计变量。根据已知条件，需要决策的是生产D1, D2, D3的量及其配方。令xij表示原料Mi生产产品Dj时的用量。

2）确立目标函数。由条件可知，理想目标是在现有原料的情况下安排3种饮料的生产，使其获得最大利润，即理想目标。由M1生产D1其获利为0（6-6）元，生产D2获利为-0.5（5.5-6.0）元，生产D3获利为-1（5.0-6.0）元，M2和M3为原料生产的各种饮料获利分别为1.5, 1, 0.5元和3, 2.5, 2元。即

其他目标根据实际情况拟定，如要保证品质，则要求严格按配方生产，即：

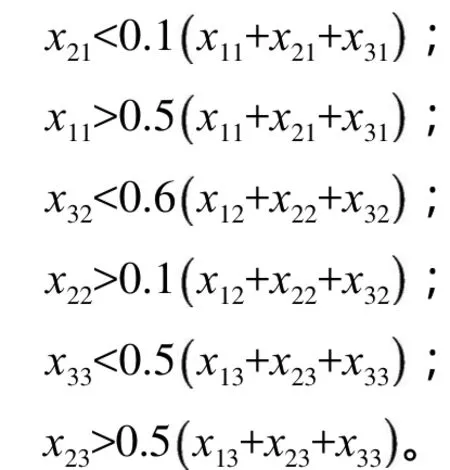
3）建立约束条件。满足每天生产2 000 L的D1饮料，这是必须满足的条件。原料的总量是有限的，即：

x11+x21+x31=2 000 ；

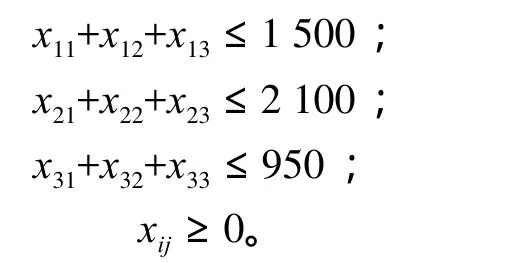
4）数学模型。将上述目标函数和约束条件综合起来，即

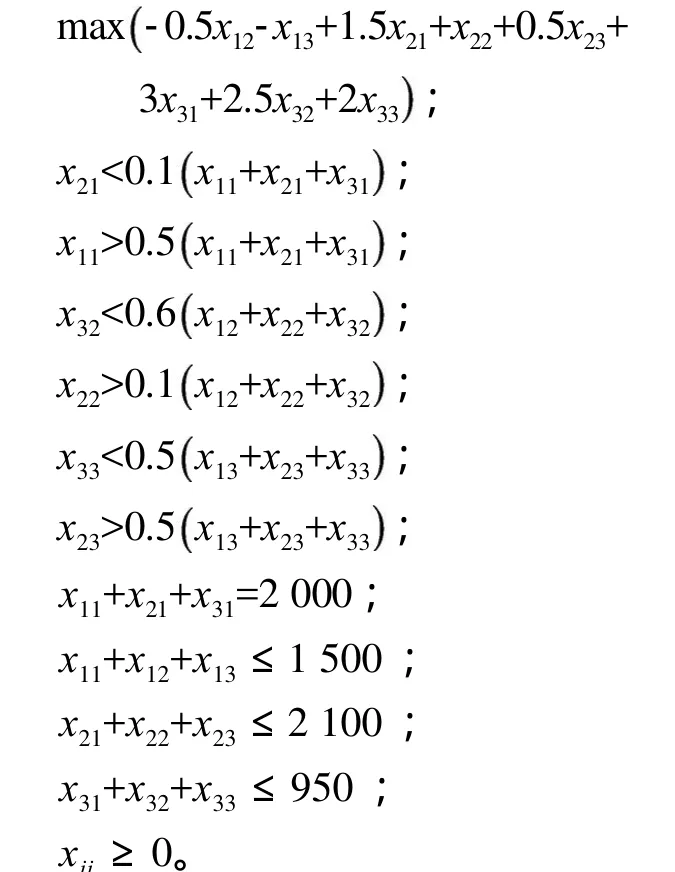
5）LINGO程序。LINGO源程序如下：

在LINGO软件中，系统默认变量大于等于零，编程时可以省略。

程序运行结果：

从运行结果可知，1 000 L的M1, 200 L的M2和800 L的M3用于生产D1饮料；1 900 L的M2和150 L的M3用于生产D2饮料；D3不安排生产；最大获利为4 975元。而文献[6]的结果为4708.3元，且D1饮料未达到2 000 L的目标。结果较文献[6]采用优先乘子模型LINDO解法满意。

例2 一作坊生产2种产品，产品A每单位产品净获利润10元，产品B每单位产品净获利润8元；A产品每单位产品需占用机器3 h，B产品为2 h，公司每周共有机器时数120 h，允许适当加班，但加班生产的各单位产品利润均降低1元。根据合同，每周2种产品各需提供30单位，怎样安排生产才能使利润最大[5]。

解 1）设计变量。根据已知条件，需要决策的是生产A, B产品的设计安排。令：

x1为产品A在正常上班时间内每周的产量；

x2为产品A在加班时间内每周的产量；

x3为产品B在正常上班时间内每周的产量；

x4为产品B在加班时间内每周的产量。

2）确立目标函数。由条件可知，理想目标是在现有的机器时间或适当的加班情况下，获得最大利润，即

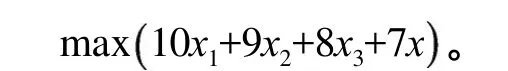
其他目标根据实际情况拟定，如在有效机器时间120 h内首先满足合同提供A, B各30个单位；其次加班时数应尽量减少，假定每周加班不超过20 h；最后利润要求每周至少为800元，等。用数学函数表示为：

3）建立约束条件。根据合同，每周2种产品各需提供30单位，这是必须满足的条件，即：

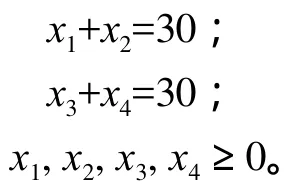
4）数学模型。将上述目标函数和约束条件综合起来，即

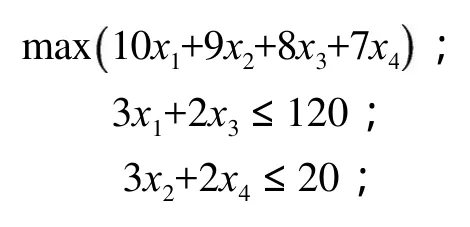
5）LINGO程序。LINGO源程序如下：

运行时提示数据溢出，把现实目标减少2个，即把加班不超过20 h和理想利润大于800元去掉，得到如下LINGO源程序：

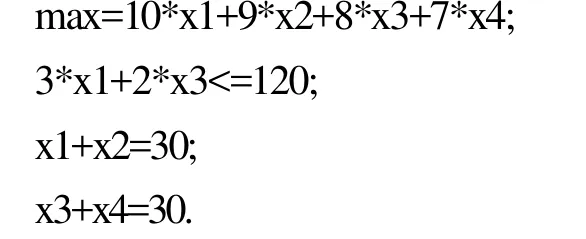
LINGO运行结果：

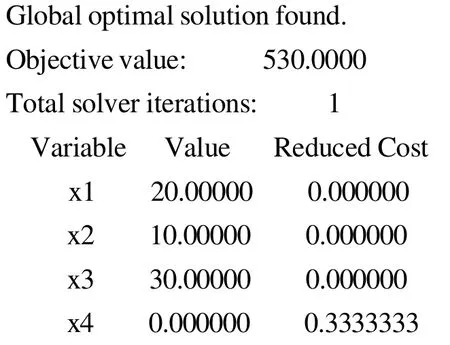
从上述计算结果可知，在正常生产时间内生产20单位A和30单位B，再安排加班时间生产10单位A，能获得530元最大利润。生产10单位A需要30小时，故最初的假设不满足，而且利润也不是最初的要求的800元，故现实目标不一定能满足，是弹性约束。结果与文献[7]中应用LINDO软件根据传统模型计算结果相同，但此方法及程序简单。

4 结语

本文应用LINGO软件，采用减少现实目标的方法求解多目标规划问题。由2个实例的求解过程可知，其过程简单，结果也优于用传统方法所得结果[6-7]。另外，在有多个理想目标时，也可将其中的n-1个转换成现实目标或约束，再用LINGO求解。该方法对其他规划问题的求解有一定的参考价值。

[1]Pareto V.Manual of Political Economy[M].New Jersey：Scholars Book Shelf，1971：92-98.

[2]Neumann J V，Morgenstern O.Theory of Games and Economic Behavior[M].London：Princeton University Press，1953：271-272.

[3]Saaty T L.The Analytic Hierarchy Process[M].New York：McGraw-Hill International，1980：241-243.

[4]Ignizio J P.Linear Programming in Single-Multiple-Objective Systems[M].New Jersey：Prentice-Hall，1982：37.

[5]卢开澄.单目标、多目标与整数规划[M].北京：清华大学出版社，1999：242-244.Lu Kaicheng.Single & Multiple Objectives and Integer Programming[M].Beijing：Tsinghua University Press，1999：242-244.

[6]洪 文.利用LINDO求解目标规划[J].安徽大学学报：自然科学版，2001，25(2) ：1-5.Hong Wen.Solve Object Programming with LINDO[J].Journal of Anhui University：Natural Science Edition，2001，25(2) ：1-5.

[7]罗罡辉，叶艳妹.多目标规划的LINDO求解方法[J].计算机运用与软件，2004，21(2) ：108-110.Luo Ganghui，Ye Yanmei.Solve Multi-Objective Goal Programming With LINDO[M].Computer Applications and Software，2004，21(2) ：108-110.